Given n points on a 2D plane, find the maximum number of points that lie on the same straight line.
当时的思路很朴素:
1.首先依次取两个点,连成一条直线(其实两个点可能相同,当时没有考虑到)
2.依次判断其他点是否在直线上。记录数量。
3.比较最大数量。
void getLine(double& a, double& b, double & c, Point pt1, Point pt2) {//ax+by+c = 0; a = pt2.y - pt1.y; b = pt1.x - pt2.x; c = pt2.x * pt1.y - pt1.x *pt2.y; } bool isOnLine(double a,double b,double c,Point pt) { if (a*a + b*b == 0) return true; double distance = abs(a*pt.x + b*pt.y + c) / sqrt(a*a + b*b); if (distance < 0.000001) return true; else return false; } int maxPoints(vector<Point>& points) { if (points.size() <= 2) return points.size(); int max = 0; for (int i = 0; i < points.size();i++) { int same = 1; for (int j = i+1; j < points.size();j++) { if (points[i].x == points[j].x && points[i].y == points[j].y) { //两个点相同 same++; continue; } double a=0, b=0, c=0; int num = 0; getLine(a, b, c, points[i], points[j]); int k = 0; while (k < points.size()) { if (isOnLine(a, b, c, points[k])) { num++; } k++; } if (max < num)max = num; } if (same == points.size()) { max = same; } } return max; }
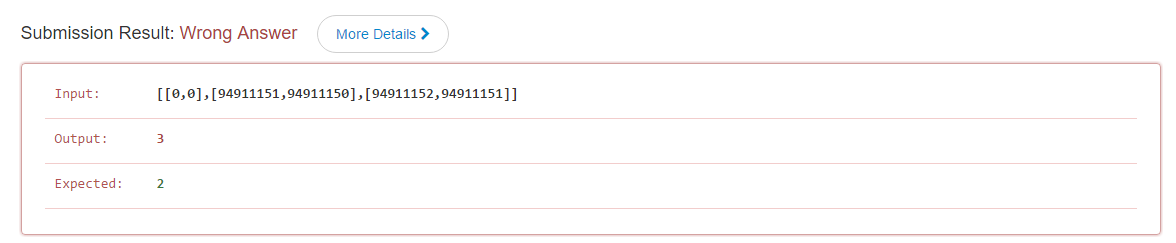
但有一个问题就是在LeetCode上没法通过。
测试用例的数值太大,导致求距离误差太小,无法表示。。。。暂时还没有好的办法。
最后,又学习了大神的代码。整理下思路。以下是大牛原话:
"For each point pi, calculate the slope of each line it forms with all other points with greater indices, i.e. pi+1, pi+2, ..., and use a map to record how many lines have the same slope (If two lines have the same slope and share a common point, then the two lines must be the same one). By doing so, you can easily find how many points are on the same line that ends at pi in O(n). Thus the amortized running time of the whole algorithm is O(n^2)."
In order to avoid using double type(the slope k) as map key, I used pair (int a, int b) as the key where a=pj.x-pi.x, b=pj.y-pi.y, and k=b/a. Using greatest common divider of a and b to divide both a, b ensures that lines with same slope have the same key.
I also handled two special cases: (1) when two points are on a vertical line (2) when two points are the same.
int maxPoints(vector<Point> &points) { if(points.size()<2) return points.size(); int result=0; for(int i=0; i<points.size(); i++) { map<pair<int, int>, int> lines; int localmax=0, overlap=0, vertical=0; for(int j=i+1; j<points.size(); j++) { if(points[j].x==points[i].x && points[j].y==points[i].y) { overlap++; continue; } else if(points[j].x==points[i].x) vertical++; else { int a=points[j].x-points[i].x, b=points[j].y-points[i].y; int gcd=GCD(a, b); a/=gcd; b/=gcd; lines[make_pair(a, b)]++; localmax=max(lines[make_pair(a, b)], localmax); } localmax=max(vertical, localmax); } result=max(result, localmax+overlap+1); } return result; }
int GCD(int a, int b) { if(b==0) return a; else return GCD(b, a%b); }