Description:
Count the number of prime numbers less than a non-negative number, n.
思路:
参考http://www.cnblogs.com/TonyYPZhang/p/5138018.html给出的方案以及wiki的方案:
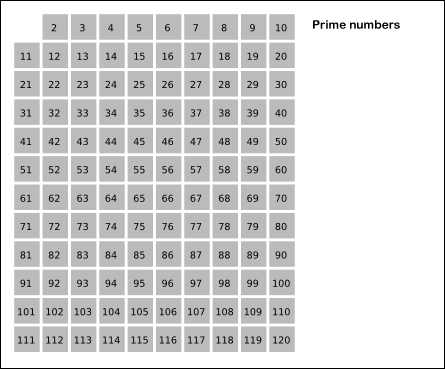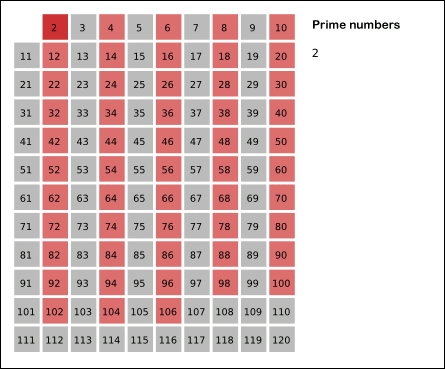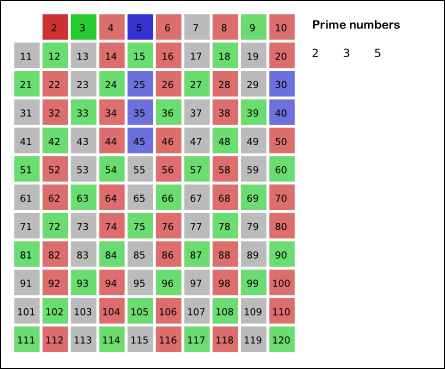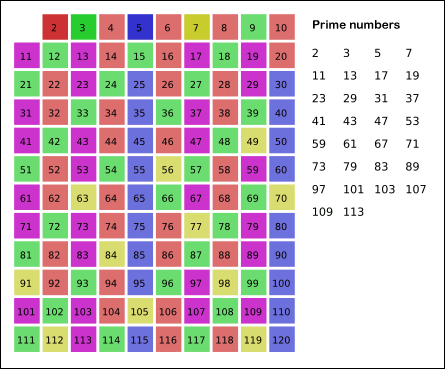
将第一个素数 2 赋值给 i。
当 i 小于 n 时:(2)
- 对于以确定的素数 i ,将 i 的全部倍数标记为合数。(1)
- 离 i 最近的下一个未被标记为合数的数即为素数。将下一个素数赋值给 i .
上面算法有可以优化的地方:
(1)步骤找合数,无需从 2 开始算 i 的倍数,而是从 i 倍开始算,即 i*i。举个例子,当 i 为 5 时, 5*2, 5*3, 5*4 的记号,已经在 i 分别为 2,3,4的时候做了。所以,可以直接从 i 倍开始算。相应地,(2)步骤也可以优化 “为 i*i < n 时”。
vector<bool> prime(n,true); for(int i =2;i*i<n;i++) { if(prime[i] == false) continue; for(int j = i*i;j<n;j+=i) { prime[j] = false; } } int ret = 0; for(int i=2;i<n;i++) { ret+=prime[i]; } return ret;