转自:https://www.cnblogs.com/mcgrady/p/3329825.html
- 什么是霍夫曼树
- 构建过程
- 编码
什么是霍夫曼树?
哈夫曼树是一种带权路径长度最短的二叉树,也称为最优二叉树。
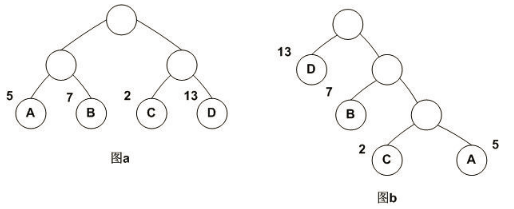
它们的带权路径长度分别为:
图a: WPL=5*2+7*2+2*2+13*2=54
图b: WPL=5*3+2*3+7*2+13*1=48
可见,图b的带权路径长度较小,我们可以证明图b就是哈夫曼树(也称为最优二叉树)。
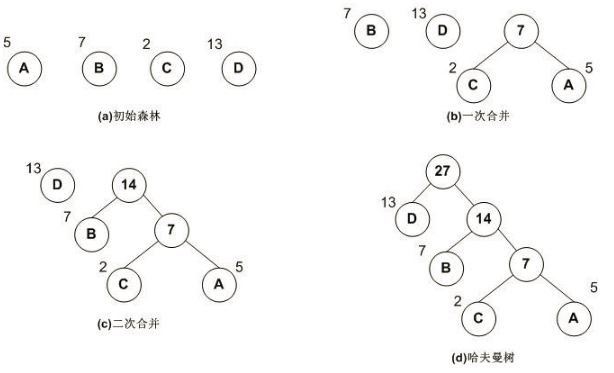
构建过程
一般可以按下面步骤构建:
1,将所有左,右子树都为空的作为根节点。
2,在森林中选出两棵根节点的权值最小的树作为一棵新树的左,右子树,且置新树的附加根节点的权值为其左,右子树上根节点的权值之和。注意,左子树的权值应小于右子树的权值。
3,从森林中删除这两棵树,同时把新树加入到森林中。
4,重复2,3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
下面是构建哈夫曼树的图解过程:
编码
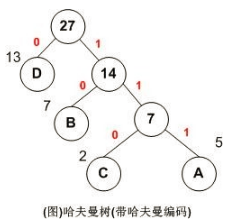
利用哈夫曼树求得的用于通信的二进制编码称为哈夫曼编码。树中从根到每个叶子节点都有一条路径,对路径上的各分支约定指向左子树的分支表示”0”码,指向右子树的分支表示“1”码,取每条路径上的“0”或“1”的序列作为各个叶子节点对应的字符编码,即是哈夫曼编码。
就拿上图例子来说:
A,B,C,D对应的哈夫曼编码分别为:111,10,110,0
用图说明如下:
记住,设计电文总长最短的二进制前缀编码,就是以n个字符出现的频率作为权构造一棵哈夫曼树,由哈夫曼树求得的编码就是哈夫曼编码。