通常用树的双亲作为并查集的存储结构,每个集合以一棵树表示,数组元素的下标代表元素名称,根节点的双亲指针为负数

并查集(Union-Find set)这个数据结构可以方便快速的解决这个问题。基本的处理思想是:初始时把每个对象看作是一个单元素集合;然后依次按顺序读入联通边,将连通边中的两个元素合并。在此过程中将重复使用一个搜索(Find)运算,确定一个集合在那个集合中。当读入一个连通边(u,v)时,先判断u和v是否在同一个集合中,如果是则不用合并;如果不是,则用一个合并(Union)运算把u、v所在集合合并,使得这两个集合中的任意两个元素都连通。因此并查集在处理时,主要用到搜索和合并两个运算。
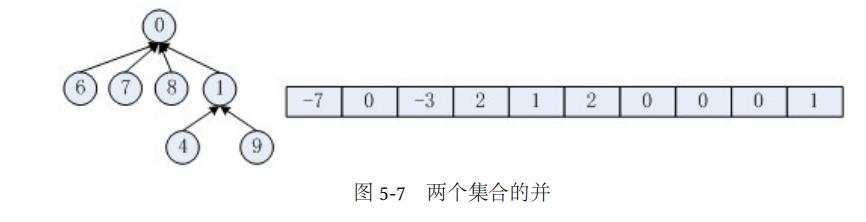
为了方便并查集的描述与实现,通常把先后加入到一个集合中的元素表示成一个树结构,并用根结点的序号来表示这个集合。因此定义一个parent[n]的数组,parent[i]中存放的就是结点i所在的树中结点i的父亲节点的序号。例如,如果parent[4]=5,就是说4号结点的父亲结点是5号结点。约定:如果i的父结点(即parent[i])是负数,则表示结点i就是它所在的集合的根结点,因为集合中没有结点的序号是负的;并且用负数的绝对值作为这个集合中所含结点的个数。例如,如果parent[7]=-4,说明7号结点就是它所在集合的根结点,这个集合有四个元素。初始时结点的parent值为-1(每个结点都是根结点,只包含它自己一个元素)。
!!!并查集可确定元素在树上

//自我实现 并查集 //a[]={1,2,3,4,5,6,7} #include<iostream> using namespace std; const maxn=100; int parent[maxn]; int n,i,j; void ufset(){ for(i=1;i<=n;i++) parent[i]=-1; } int find(int x){ int s; for(s=x;parent[x]>=0;s=parent[s]); return s; } //将两个不同集合元素进行合并,使两个集合任意两元素可以连通 void Union(int R1,int R2){ int r1=find(R1),r2=find(R2); int tmp=parent[r1]+parent[r2];//负数 if(parent[r1]>parent[r2]) { parent[r1]=r2; parent[r2]=tmp; } else { parent[r2]=r1; parent[r1]=tmp; } } int main() { }
其中find函数可以优化作压缩路径处理

int find2(int x){ int s; for(s=x;parent[s]>=0;s=parent[s]); while(x!=s){ int tmp=parent[x]; parent[x]=s; x=tmp; //递推 }
