算法笔记——【动态规划】矩阵连乘问题——备忘录法

      问题描述：给定n个矩阵：A1,A2,...,An，其中Ai与Ai+1是可乘的，i=1，2...，n-1。确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。输入数据为矩阵个数和每个矩阵规模，输出结果为计算矩阵连乘积的计算次序和最少数乘次数。

      问题解析：由于矩阵乘法满足结合律，故计算矩阵的连乘积可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定，也就是说该连乘积已完全加括号，则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。

       完全加括号 的矩阵连乘积可递归地定义为：

     （1）单个矩阵是完全加括号的；

     （2）矩阵连乘积A是完全加括号的，则A可表示为2个完全加括号的矩阵连乘积B和C的乘积并加括号，即A=(BC)

       例如，矩阵连乘积A1A2A3A4有5种不同的完全加括号的方式：(A1(A2(A3A4)))，(A1((A2A3)A4))，((A1A2)(A3A4))，((A1(A2A3))A4)，(((A1A2)A3)A4)。每一种完全加括号的方式对应于一个矩阵连乘积的计算次序，这决定着作乘积所需要的计算量。

      看下面一个例子，计算三个矩阵连乘{A1，A2，A3}；维数分别为10*100 , 100*5 , 5*50 按此顺序计算需要的次数((A1*A2)*A3):10X100X5+10X5X50=7500次，按此顺序计算需要的次数(A1*(A2*A3)):100*5*50 + 10*100*50 = 75000次（注意计算次数的方法 ！  ）

      所以问题是：如何确定运算顺序，可以使计算量达到最小化。      

　  算法思路：

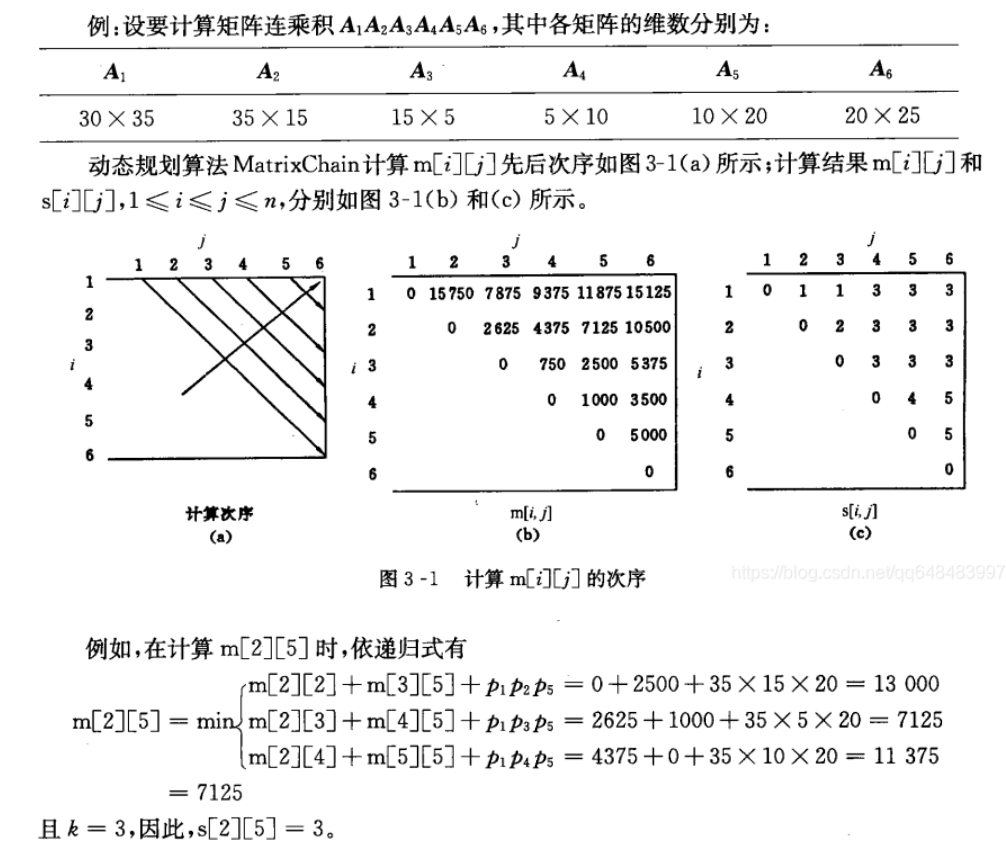
      例：设要计算矩阵连乘乘积A1 A2 A3 A4 A5 A6，其中各矩阵的维数分别是：

      A1：30*35;     A2：35*15;     A3：15*5;     A4：5*10;     A5：10*20;     A6：20*25 

      递推关系：

      设计算A[i:j]，1≤i≤j≤n，所需要的最少数乘次数m[i,j]，则原问题的最优值为m[1,n]。

      当i=j时，A[i:j]=Ai，因此，m[i][i]=0，i=1,2,…,n
      当i<j时，若A[i:j]的最优次序在Ak和Ak+1之间断开，i<=k<j,则：m[i][j]=m[i][k]+m[k+1][j]+pi-1pkpj。由于在计算是并不知道断开点k的位置，所以k还未定。不过k的位置只有j-i个可能。因此，k是这j-i个位置使计算量达到最小的那个位置。

      综上，有递推关系如下：

　　若将对应m[i][j]的断开位置k记为s[i][j]，在计算出最优值m[i][j]后，可递归地由s[i][j]构造出相应的最优解。s[i][j]中的数表明，计算矩阵链A[i:j]的最佳方式应在矩阵Ak和Ak+1之间断开，即最优的加括号方式应为(A[i:k])(A[k+1:j)。

因此，从s[1][n]记录的信息可知计算A[1:n]的最优加括号方式为(A[1:s[1][n]]) (A[   s[1][n]+1  :  n] )，进一步递推，A[1:s[1][n]]的最优加括号方式为(A[1:s[1][s[1][n]]])(A[s[1][s[1][n]]+1:s[1][s[1][n]]])。同理可以确定A[ s[1][n]+1 :n]的最优加括号方式在s[ s[1][n]+1 ][n]处断开...照此递推下去，最终可以确定A[1:n]的最优完全加括号方式，及构造出问题的一个最优解：

如下例题：

          

    

　　备忘录递归算法

     备忘录方法用表格保存已解决的子问题答案，在下次需要解决此子问题时，只要简单查看该子问题的解答，而不必重新计算。备忘录方法为每一个子问题建立一个记录项，初始化时，该记录项存入一个特殊的值，表示该子问题尚未求解。在求解的过程中，对每个带求的子问题，首先查看其相应的记录项。若记录项中存储的是初始化时存入的特殊值，则表示该问题是第一次遇到，此时计算出该子问题的解，并将其保存在相应的记录项中，以备以后查看。若记录项中存储的已不是初始化时存入的特殊值，则表示该子问题已被计算过，相应的记录项中存储的是该子问题的解答。此时从记录项中取出该子问题的解答即可，而不必重新计算。

 

//A1 30*35 A2 35*15 A3 15*5 A4 5*10 A5 10*20 A6 20*25
//p[0-6]={30,35,15,5,10,20,25} 

#include<iostream>
using namespace std;

#define N 7  //N为7，实际表示有6个矩阵
int p[N]={30,35,15,5,10,20,25};
int m[N][N],s[N][N];

int LookupChain(int i, int j){
    if(m[i][j]>0)
        return m[i][j];
    if(i == j)
        return 0;
    m[i][j] = LookupChain(i,i) + LookupChain(i+1,j)+p[i-1]*p[i]*p[j];
    s[i][j] = i;
    for(int k=i+1; k<j;k++){
        int t = LookupChain(i,k)+LookupChain(k+1,j)+p[i-1]*p[k]*p[j];
        if(t<m[i][j]){
            m[i][j]=t;
            s[i][j]=k;
        }
    }
    return m[i][j];
}

int MemorizedMatrixChain(int n, int m[][N], int s[][N]){
    for(int i=1;i<=n;i++){  //初始化默认都是0
        for(int j=1;j<=n;j++)
            m[i][j] = 0;
    }
    return LookupChain(1,n);
}
/*
*追踪函数：根据输入的i,j限定需要获取的矩阵链的始末位置，s存储断链点
*/
void Traceback(int i,int j, int s[][N]){
    if(i==j)       //回归条件
    {
        cout<<"A"<<i;
    }
    else       //按照最佳断点一分为二，接着继续递归
    {
        cout<<"(";
        Traceback(i,s[i][j],s);
        Traceback(s[i][j]+1,j,s);
        cout<<")";
    }
}
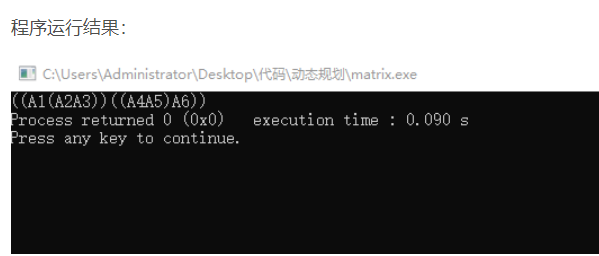
int main(){


    MemorizedMatrixChain(N-1,m,s);//N-1因为只有六个矩阵
    Traceback(1,6,s);
    return 0;
}

　参考： https://blog.csdn.net/qq648483997/article/details/93063764 

　　　　https://blog.csdn.net/liufeng_king/article/details/8497607

  　　　　https://www.cnblogs.com/lixing-nlp/p/7688989.html  老师的课件内容