BZOJ5131: [CodePlus2017年12月]可做题2

BZOJ没有题面，差评

洛谷的题目链接

题解

其实这题很久之前就写了，也想写个题解但是太懒了，咕到了今天

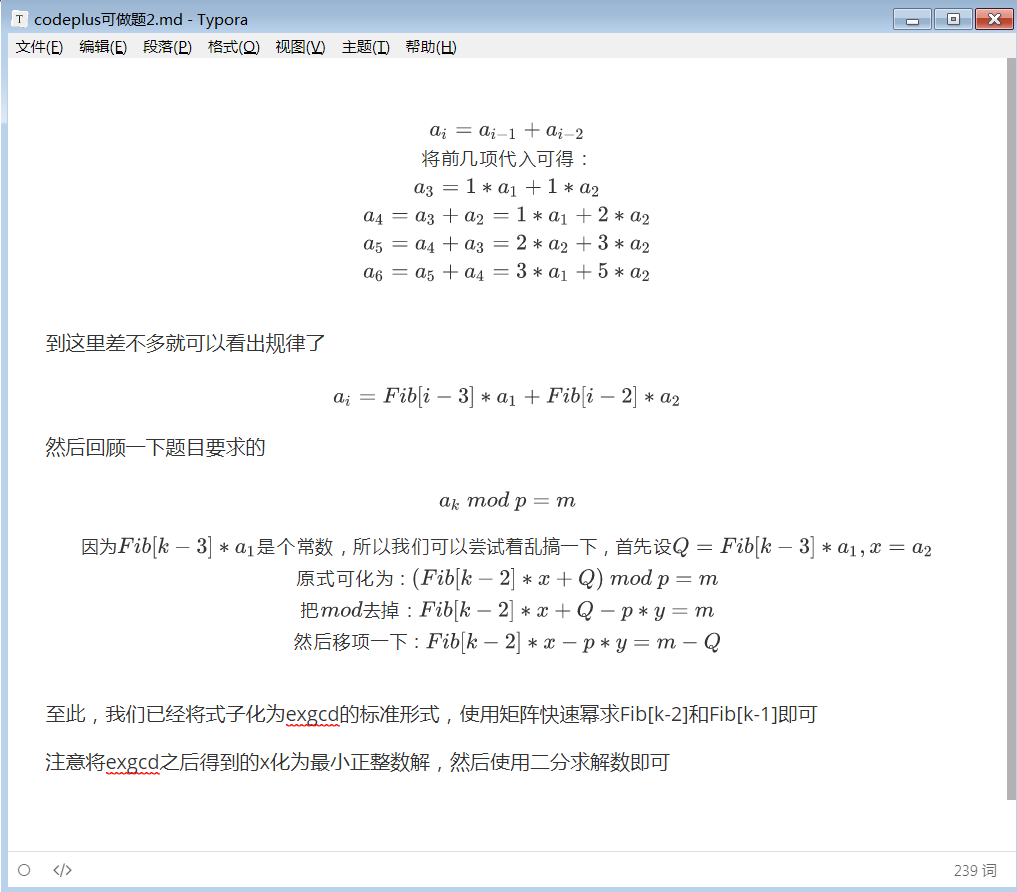
在typora写完题解不想copy过来再改格式了，于是直接贴截图qwq

#include <bits/stdc++.h>

#define ll long long
#define inf 0x3f3f3f3f
#define il inline
#define int long long

namespace io {

    #define in(a) a=read()
    #define out(a) write(a)
    #define outn(a) out(a),putchar('
')

    #define I_int int
    inline I_int read() {
        I_int x = 0 , f = 1 ; char c = getchar() ;
        while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
        while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
        return x * f ;
    }
    char F[ 200 ] ;
    inline void write( I_int x ) {
        if( x == 0 ) { putchar( '0' ) ; return ; }
        I_int tmp = x > 0 ? x : -x ;
        if( x < 0 ) putchar( '-' ) ;
        int cnt = 0 ;
        while( tmp > 0 ) {
            F[ cnt ++ ] = tmp % 10 + '0' ;
            tmp /= 10 ;
        }
        while( cnt > 0 ) putchar( F[ -- cnt ] ) ;
    }
    #undef I_int

}
using namespace io ;

using namespace std ;

#define N 100010

int a1 , l , r , k , p , m ;
struct matrix {
    int m[2][2] ;
    matrix() { memset(m,0,sizeof(m)); }
    matrix operator * (const matrix &x) {
        matrix ans;
        for(int i = 0 ; i < 2 ; i ++) {
            for(int j = 0 ; j < 2 ; j ++) {
                for(int k = 0 ; k < 2 ; k ++) {
                    ans.m[i][j] = (ans.m[i][j] + m[i][k] * x.m[k][j]) % p ;
                }
            }
        }
        return ans ;
    }
} base , ans ;

void power(int b) {
    base.m[0][0] = base.m[1][0] = base.m[0][1] = 1 ; base.m[1][1] = 0 ;
    ans.m[0][0] = ans.m[1][1] = 1 ; ans.m[1][0] = ans.m[0][1] = 0 ;
    while(b) {
        if(b&1) ans = ans * base ;
        base = base * base ;
        b >>= 1;
    }
}

int x , y ;
int exgcd(int a , int b) {
    if(b == 0) { x = 1 ; y = 0 ; return a ; }
    int Ans = exgcd(b , a % b) , t = x ;
    x = y ; y = t - (a / b) * y ;
    return Ans ;
}

int find(int x , int t) {
    int l = 0 , r = t / p + 1 ;
    while(l <= r) {
        int mid = (l + r) >> 1 ;
        if(x + p * mid >= t) r = mid - 1 ;
        else l = mid + 1 ;
    }
    return l ;
}

signed main() {
    int T = read() ;
    while(T--) {
        a1 = read() , l = read() , r = read() , k = read() , p = read() , m = read() ;
        a1 %= p ; power(k - 2) ;
        int mod = (m - a1 * ans.m[1][0] % p + p) % p ;
        int gcd = exgcd(ans.m[0][0] , p) ;
        if(mod % gcd != 0) { puts("0") ; continue ; }
        x = x * (mod/gcd) ; p /= gcd ; x = (x % p + p) % p ;
        outn( find(x , r+1) - find(x , l) ) ;
    }
}