[bzoj2721][Violet 5]樱花

题目链接

数论好（难）题

题目要求求出$1/x+1/y=1/n!$ 中$x$和$y$的正整数解的个数

那么我们可以化简一下

很简单就可以化出$(x+y)n!=xy$

但是并没有化掉任何一个未知数，所以这玩意没用

在这个基础上再化简一下

因为$x,y$均为正整数且均$>n!$

所以可以设$y=n!+k$

那么原式可化为$(x+n!+k)n!=x(n!+k)$

再整理一下（这里给出运算步骤）

$xn!+(n!)^2+kn!=xn!+kx$

$x=((n!)^2+kn!)/k$

$x=(n!)^2/k+n!$

于是我们向正解迈出了一大步

由题可知，$x,y,n!$均为整数，所以$k$也是整数（如果$k$不是整数，$x$也不会是整数）

然后由这个式子$x=(n!)^2/k+n!$我们可以知道，$k$一定是$(n!)^2$的一个因数，否则会不符合x是整数这个定义

且易得$x$和$k$是一一对应的

那么至此，这个问题就变成了，求$(n!)^2$的因数的个数

用一下欧拉筛法筛出质数，算出质数的每个幂对于我们所求的答案的贡献就可以了

这几天又重新写了一下这题，还是不会...

不知道是换元的话根本不会写

不过还是放一下我的推导过程吧：

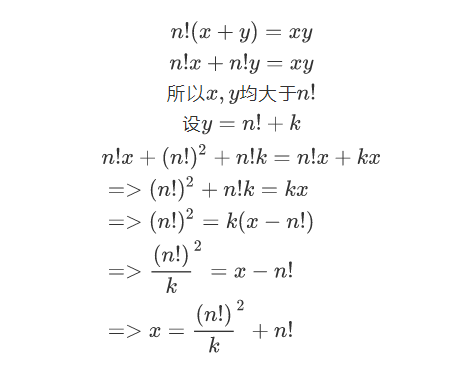
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
using namespace std;

#define N 1000010
#define ll long long 
#define inf 2147483647
const int mod = 1e9 + 7;
ll cnt[N], ans = 1;
int vis[N], p[N], tot, n; 

int main() {
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
#endif
    scanf("%d", &n);
    for(int i = 2; i <= n; ++i) {
        if(!vis[i]) p[++tot] = i;
        for(int j = 1; j <= tot && p[j] * i <= n; ++j) {
            vis[i * p[j]] = 1;
            if(i % p[j] == 0) break;
        }
    }
    for(int i = 1; i <= tot; i ++) {
        ll tmp = p[i];
        for(; tmp <= n; tmp *= 1ll * p[i]) cnt[i] += 1ll * (n / tmp);
        cnt[i] %= mod;
    }
    for(int i = 1; i <= tot; i ++) {
        ans = 1ll * ans * (2 * cnt[i] + 1) % mod; 
    }
    printf("%lld
", ans);
    return 0;
}

感谢学长qzz的解惑qwq，学长的博客里也有这道题的题解如果我讲的不是很清楚，可以私信问我或者看下学长的博客=v=