二叉树的删除操作,其中删除最小值最大值比较容易,就是一直不停的遍历二叉树的左子树和右子树,一直找到没有其左子树和右子树。然后直接将其删除就可以了
一、删除最小值(假定这个二叉树的构造是左节点小于父节点,右节点大于父节点):从根节点开始遍历,如果有左子树就继续遍历左子树,直至没有左节点为止
代码如下
public void deleteMin() { root = deleteMin(root); } private Node deleteMin(Node x) { if (x.left == null) return x.right; x.left = deleteMin(x.left); x.size = size(x.left) + size(x.right) + 1; return x; }
删除最大值也是一样的思想,只不过是遍历右子树:
public void deleteMax() { root = deleteMax(root); } private Node deleteMax(Node x) { if (x.right == null) return x.left; x.right = deleteMax(x.right); x.size = size(x.left) + size(x.right) + 1; return x; }
二、删除节点操作(假定这个二叉树的构造是左节点小于父节点,右节点大于父节点):
- 将指向即将被删除的结点的链接保存为t;
- 将x指向它的后继结点min(t.right);
- 将x的右链接(原本指向一颗所有结点都大于x.key的二叉查找树)指向deleteMin(t.right),也就是在删除后所有结点仍然都大于x.key的子二叉查找树;
- 将x的左链接(本为空)设为t.left(其下所有的键都小于被删除的结点和他的后继节点)。
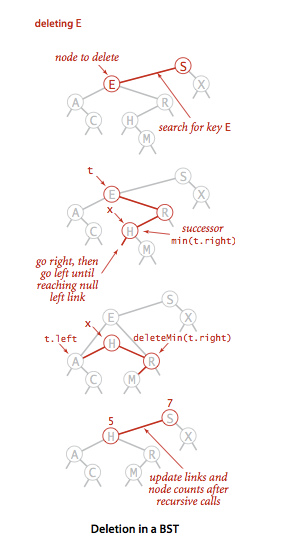
代码:
public void delete(Key key) { root = delete(root, key); } private Node delete(Node x, Key key) { if (x == null) return null; int cmp = key.compareTo(x.key); if (cmp < 0) x.left = delete(x.left, key); else if (cmp > 0) x.right = delete(x.right, key); else { if (x.right == null) return x.left; if (x.left == null) return x.right; Node t = x; x = min(t.right); x.right = deleteMin(t.right); x.left = t.left; } x.size = size(x.left) + size(x.right) + 1; return x; }