【Luogu】P3369 【模板】普通平衡树（树状数组）

P3369 【模板】普通平衡树（树状数组）

一、树状数组

树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。

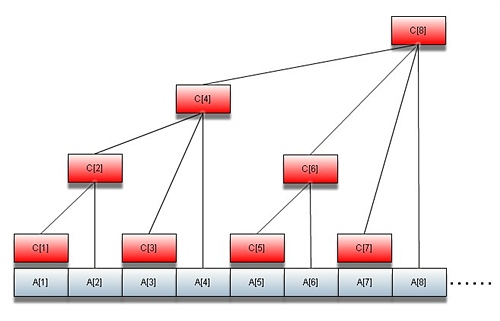
这张图总是让很多初学者望而生畏（好吧只是我）
所以在学习它之前，我们来看看线段树。

（现在我默认大家都会线段树）
我们知道如果(a + b = c)，则(b = c - a)。
所以，所有节点的右儿子都是不需要的。

我们把线段树上不必要的节点去掉。
它长得会像这样。

这种数据结构我们称它为树状数组。可以发现所有线段的右断点都互不相同，所以我们把它按右端点重新编号。

可以发现一些性质：

1. 节点(p)的父亲即为(p + lowbit(p))。（(lowbit(x) = x and -x)）
2. 节点(p)的线段长度为(lowbit(p))

故我们可以写出给一个数加(x)的代码。即顺着边依次更行它的祖先。

void update(int x, int y) {
	for (int i = x; i <= n; i += lowbit(i)) c[i] += y;
}

我们还需要查询([l, r])的和，即为([1, r])的和 (-) ([1, l - 1])的和。
下面有一个求([1, x])的和的代码。

void query(int x) {
	int ret = 0;
	for (int i = x; i; i -= lowbit(i)) ret += c[i];
	return ret;
}

我们再根据树状数组的图可以发现其实就是对x进行二进制拆分。
求出每一段的和。

二、这道题的解释

我们可以考虑类似计数的方法。即如果(x)比较小，我们可以用(num[x])表示(x)出现的次数。所以查找排名即为查询比(x)小的数的(num)和。

三、Kth()

我们考虑在树状数组上进行类似倍增的操作。

int _kth(int k) {
	int ret = 0, sum = 0;
        for (int i = 20; i >= 0; --i)
        	if (ret + (1 << i) <= lcnt && sum + c[ret + (1 << i)] < k) {
                	sum += c[ret + (1 << i)];
                	ret += 1 << i;
		}
	for (int i = 0; i <= 20; ++i)
		if (sum + c[ret + (1 << i)] >= k) {
			ret += 1 << i;
			break;
		}
        return ret;
}

简单地说，就是先跳大的，再跳最小一步使刚好大于等于k。

四、代码

#include <stdio.h>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 100005;
int n, opt[MAXN], num[MAXN], lcnt, lsh[MAXN];
class BinaryIndexTree {
    private:
        int c[MAXN];
        int _kth(int k) {
			int ret = 0, sum = 0;
			for (int i = 20; i >= 0; --i)
				if (ret + (1 << i) <= lcnt && sum + c[ret + (1 << i)] < k) {
                	sum += c[ret + (1 << i)];
                	ret += 1 << i;
			}
			for (int i = 0; i <= 20; ++i)
				if (sum + c[ret + (1 << i)] >= k) {
					ret += 1 << i;
					break;
				}
            return ret;
        }
        void _insert(int x) {
            for (int i = x; i <= n; i += i & -i) ++c[i];
        }
        void _erase(int x) {
            for (int i = x; i <= n; i += i & -i) --c[i];
        }
        int num(int x) {
            int ret = 0;
            for (int i = x; i; i -= i & -i) ret += c[i];
            return ret;
        }
    public:
        int kth(int k) { return _kth(k); }
        void insert(int x) { _insert(x); }
        void erase(int x) { _erase(x); }
        int rank(int x) { return num(x - 1) + 1; }
        int pre(int x) { return _kth(num(x - 1)); }
        int suc(int x) { return _kth(num(x) + 1); }
} bitree;
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d%d", &opt[i], &num[i]);
        if (opt[i] != 4) lsh[++lcnt] = num[i];
    }
    sort(lsh + 1, lsh + lcnt + 1);
    lcnt = unique(lsh + 1, lsh + lcnt + 1) - lsh - 1;
    for (int i = 1; i <= n; ++i) {
        if (opt[i] == 4) {
            printf("%d
", lsh[bitree.kth(num[i])]);
        } else {
            int x = lower_bound(lsh + 1, lsh + lcnt + 1, num[i]) - lsh;
            if (opt[i] == 1) bitree.insert(x);
            else if (opt[i] == 2) bitree.erase(x);
            else if (opt[i] == 3) printf("%d
", bitree.rank(x));
            else if (opt[i] == 5) printf("%d
", lsh[bitree.pre(x)]);
            else if (opt[i] == 6) printf("%d
", lsh[bitree.suc(x)]);   
        }
    }
    return 0;
}