数据结构
决定数据存储于内存时数据顺序和位置关系
链表
蓝黄红三个字符串被存储在链表中,每个数据都有存储一个指向下一个数据内存地址的“指针”
因为有指针索引,链表结构的数据可以分散在存储空间中,无需连续。
也因存储是分散的,如果要访问数据,只能从第一个数开始向下逐个访问。
比如要找到红就要蓝→黄→红
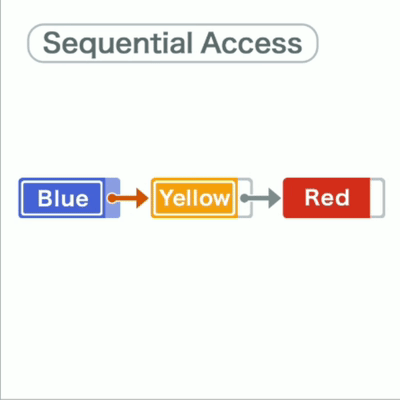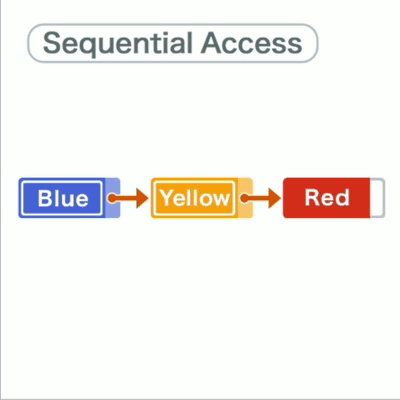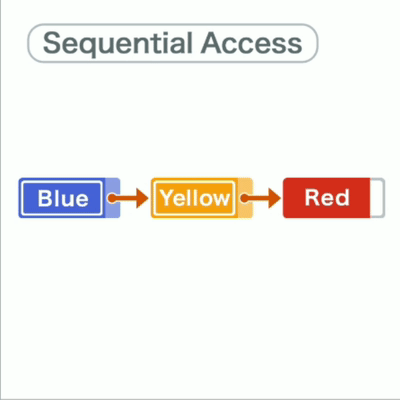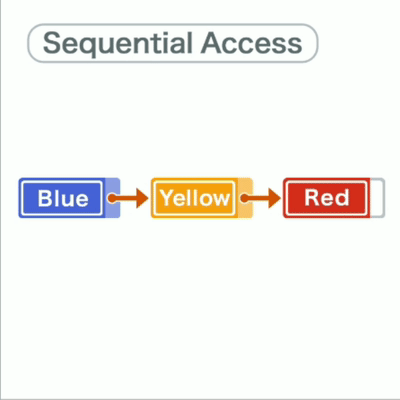
链表指针
得益于有指针指向,若要在链表中加入数据,只需要改变插入位置前后的指针就可以
比如在蓝黄间加入绿,只要把绿指针指向黄,蓝指针指向绿
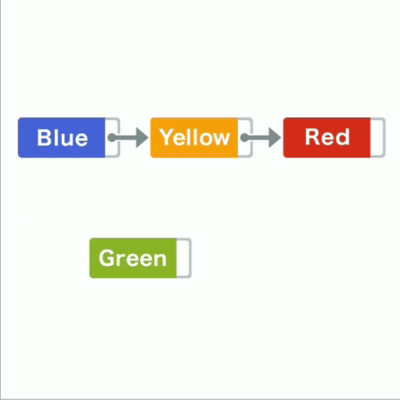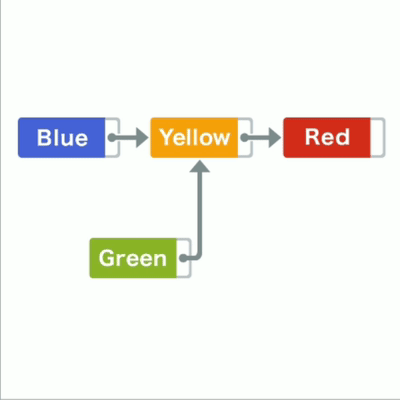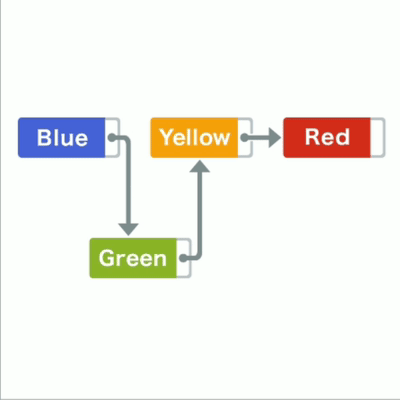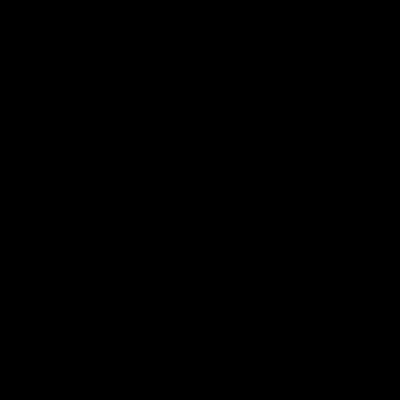
链表插入
要删除时,比如删除黄只要把绿指针由黄改为指向红,黄不变等日后被覆盖即可
查找时间复杂度O(n)
添加时间复杂度O(1)
--------------------------------------------------------------------------------
数组
在数组中数据按顺序存储在内存的连续空间内,每个数据的内存地址可以通过数组下标算出,可以随机访问目的数据

随机访问
相比可以方便的随机访问,要在数组中添加数据就比较复杂了
比如要在数组的蓝黄之间添加绿
首先在数组末尾添加所要增加的存储空间
再把已有的数据一个个往后移
最后在空出来的位置上写入

数组插入
同样删除绿,先将绿移除,再将后面的数据一个个往前移,最后删除多余的空间
查找时间复杂度O(1)
添加时间复杂度O(n)
--------------------------------------------------------------------------------
栈
在栈这种结构中,我们只能访问最新添加的数据,就像一堆东西层层叠放,只能从最上面拿取。
栈形象
往栈里添加数据的操作,入栈push;从栈中取出数据的操作,出栈pop。
这种就叫后进先出的结构,Last In First Out (LIFO)
在栈中,添加和删除数据的操作只能在一端进行,访问数据也只能访问到顶端的数据。
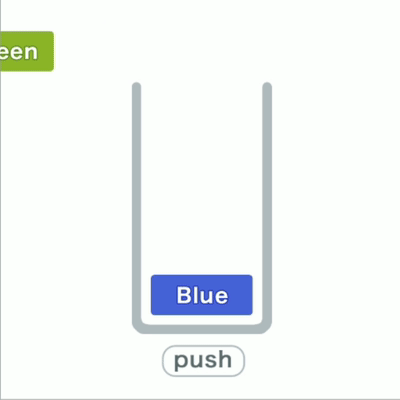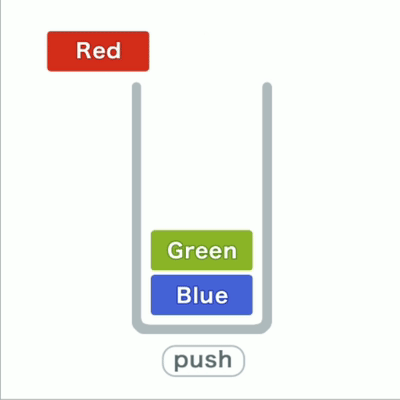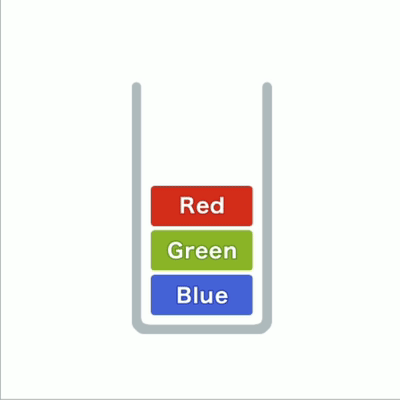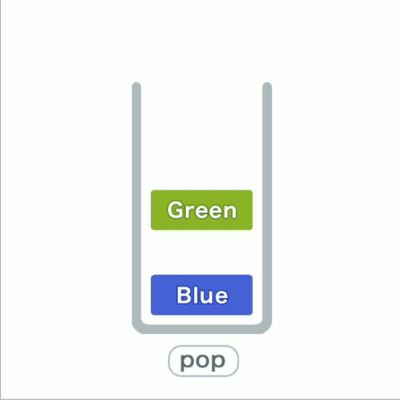
栈出入
--------------------------------------------------------------------------------
队列
队列顾名思义,就像是排成一 队的人。在队列中,处理总是从第一名开始往后进行,而新来的人只能排在队尾

队列形象
往队列里添加数据的操作,入队;从队列中取出数据的操作,出队
这种就叫先进先出的结构,First In First Out (FIFO)

队列出入
在栈中,数据的添加和删除都在同一端进行,而在队列中则分别是在两端进行的。
队列也不能直接访问位于中间的数据,必须通过出队操作将目标数据变成首位后才能访问
--------------------------------------------------------------------------------
哈希表
哈希表存储由键值组成,key、value。比如在这里把姓名为键,把性别为值。

哈希表
如果这些键值对存储在数组中,为了检索到Ally的性别,在数组中只能重头开始查询。

线性查找
数据量越多,这种线性查找所耗费的时间就越长。所以说数据的查询较为耗时,不是大量存储
在哈希表中,
首先准备好数组,用哈希函数计算每个数据的键,得到字符串的哈希值,
再将得到的哈希值除以数组的长度,求的余数即mod运算,
最后将数据存放相应的数组位置中
若存储位置重复,则可以使用链表在已有的数据后面存储
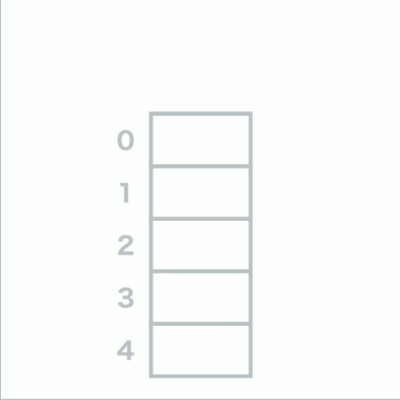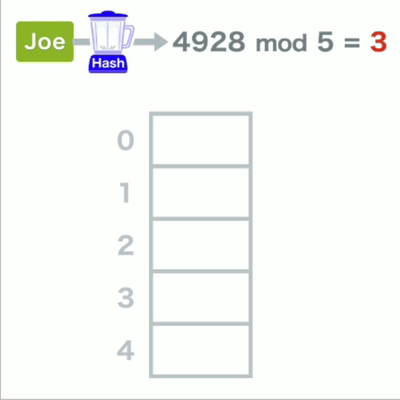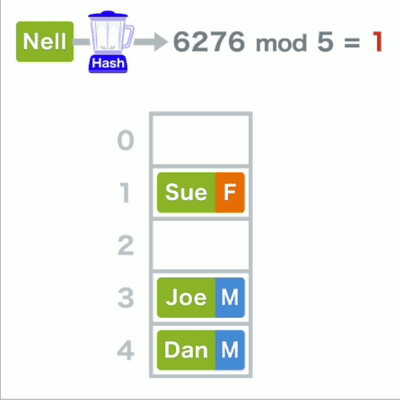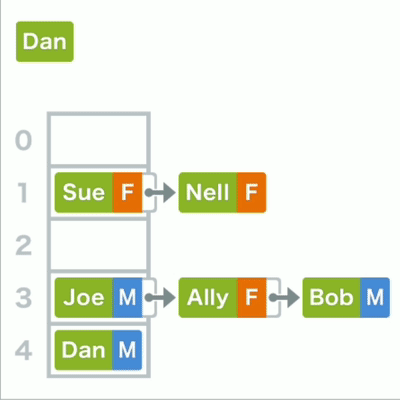
哈希录入
查询哈希表中的数据时为 了找到它的存储位置,先要算出键的哈希值,再对其进行mod运算,最终得到的结果。若所对应的还不是目标,则在其所在的链表中继续线性查找。
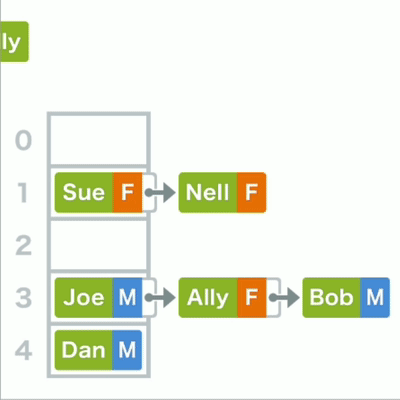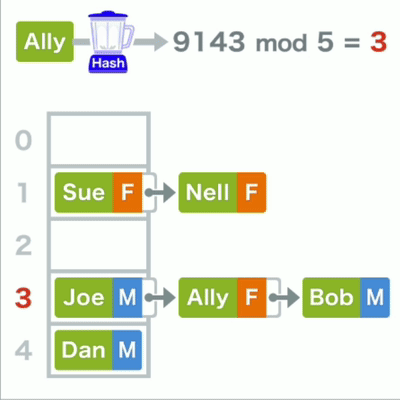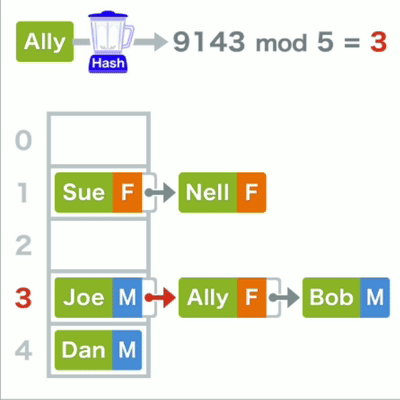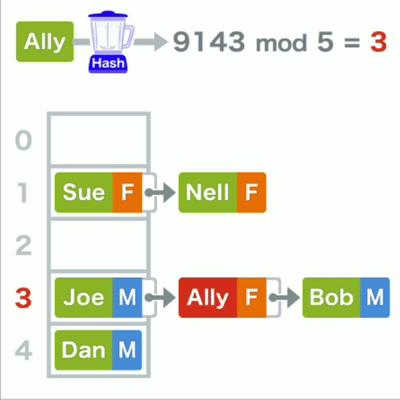
哈希查找
--------------------------------------------------------------------------------
堆
堆是一种图的树形结构,被用于实现“优先队列”(priority queues)
优先队列是一种数据结构,可以自由添加数据,但取出数据时要从最小值开始按顺序取出。
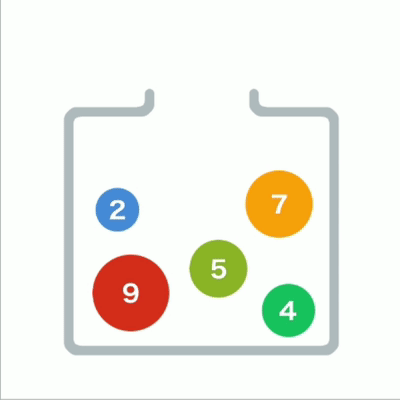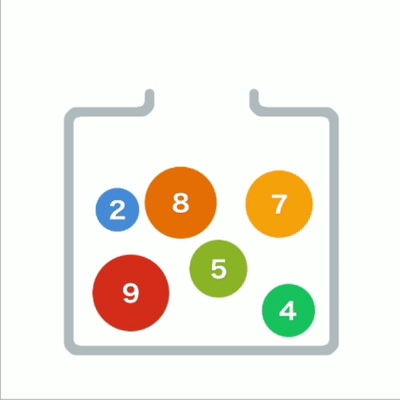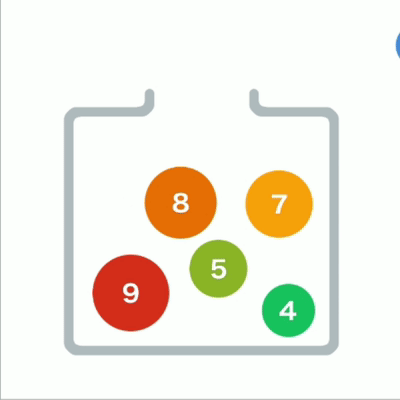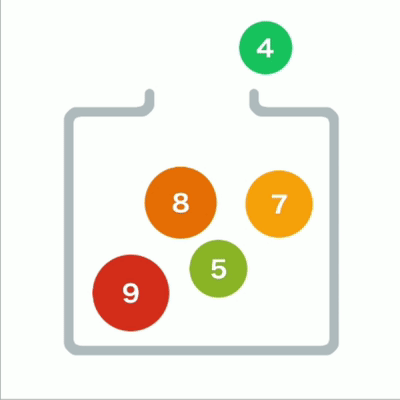
堆形象
在堆的树形结构中,各个顶点被称为“结点”(node),数据就存储在这些结点中。
结点内的数字就是存储的数据
堆中的每个结点最多有两个子结点
树的形状取决于数据的个数
结点的排列顺序为从上到下,同一行里则为从左到右。
在堆中存储数据时必须遵守:子结点必定大于父结点,因此,最小值被存储在顶端的根结点中。
往堆中添加数据时,为了遵守这条规则,一般会把新数据放在最下面一行靠左的位置。当最下面一
行里没有多余空间时,就再往下另起一行, 把数据加在这一行的最左端。如果父结点大于子结点,则不符合规则,因此需要交换父子结点的位置。
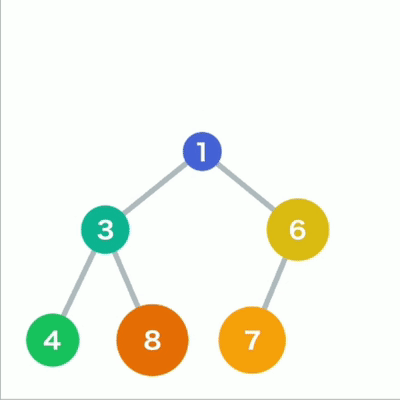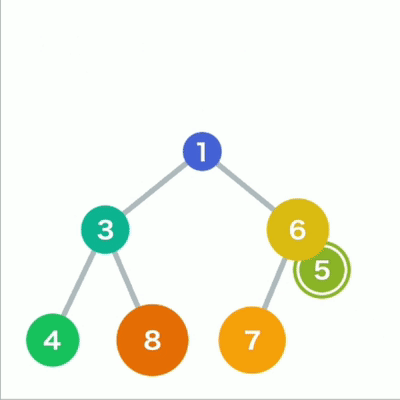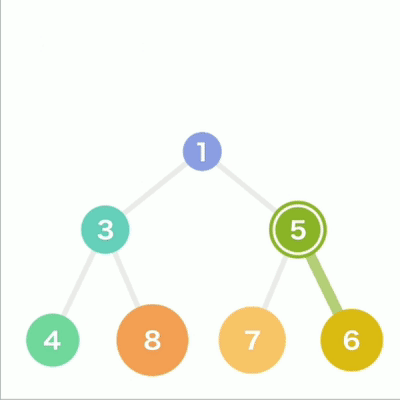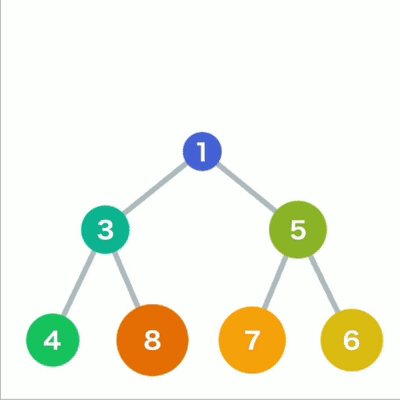
堆插入
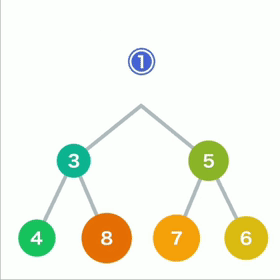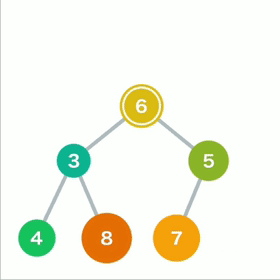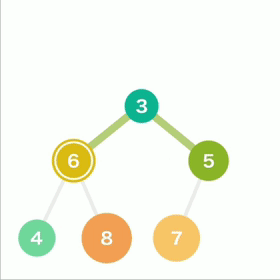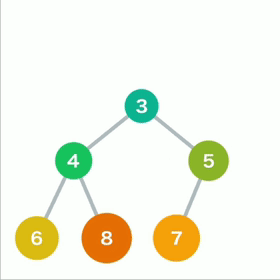
从堆中取出数据时,取出的是最上面的数据。这样,堆中就能始终保持最上面的数据最小。
当最上面的数据被取出,堆的结构要重新调整。
先将最后的数据移动到最顶端
如果子结点的数字小于父结点,则将父结点和左右两个结点中较小的一个进行交换。重复操作直到数据都符合规则,不再需要交换为止。
取出最小值的时间复杂度 O(1)
重构树的时间复杂度 O(logn)
添加数据需要的运行时间与树的高度成正比,也是 O(logn)
堆导出
--------------------------------------------------------------------------------
二叉查找树
二叉查找树采用了图的树形结构,数据存储于二叉查找树的各个结点中
二叉查找树有两个性质。
第一个是每个结点的 值均大于其左子树上任意一个结点的值。
比如结点9大于其左子树上的3和8。同样,结点15也大于其左子树上任意一个结点的值。
第二个是每个结点的值均小于其右子树上任意 一个结点的值。比如结点 15 小于其右子树上的 23、17和28。
所以二叉查找树的最小结点要从顶端开始,往其左下的末端寻找。
反过来,二叉查找树的最大结点要从顶端开始,往其右下的末端寻找。
若要往二叉查找树中添加数
首先,从二叉查找树的顶端结点开始寻找添加数字的位置。将想要添加的1与该结点中的值进行比较,小于它则往左移,大于它则往右移。
如果需要删除的结点没有子结点,直接删掉该结点即可
如果需要删除的结点只有一个子结点,那么先删掉目标结点,然后把子结点移到被删除结点的位置上即可。
如果需要删除的结点有两个子结点,那么先删掉目标结点,然后在被删除结点的左子树中寻找最大结 点,最后将最大结点移到被删除结点的位置上。
在二叉查找树中查找结点,从二叉查找树的顶端结点开始往下查找,小于该结点的值则往左移,大于则往右移。
--------------------------------------------------------------------------------