[AI] 最近邻KNN 及平衡KD 树 学习笔记

最近邻算法KNN 学习笔记

定义

为了判定未知样本的类别，以全部训练样本作为代表点，计算未知样本与所有训练样本的距离，并以最近邻者的类别作为决策未知样本类别的唯一依据。
选择未知样本一定范围内确定个数的K个样本，该K个样本大多数属于某一类型，则未知样本判定为该类型。

说明

一般分类方法：
•积极学习法 (决策树归纳)：先根据训练集构造出分类模型，根据分类模型对测试集分类。
•消极学习法 (基于实例的学习法):推迟建模，当给定训练元组时，简单地存储训练数据(或稍加处理)，一直等到给定一个测试元。
KNN就是一种简单的消极学习分类方法，它开始并不建立模型，没有显式的学习过程。
K近邻模型由三个基本要素组成：
•距离度量（邻居判定标准）
•K值的选择（邻居数量）
•分类决策规则（确定所属类别）

算法基本步骤：

1. 计算待分类点与已知类别的点之间的距离
2. 按照距离递增次序排序
3. 选取与待分类点距离最小的k个点
4. 确定前k个点所在类别的出现次数
5. 返回前k个点出现次数最高的类别作为待分类点的预测分类

K值的选择

如何选择一个最佳的K值取决于数据。一般情况下，在分类时较大的K值能够减小噪声的影响，但会使类别之间的界限变得模糊。

如果k取3，从图可见，待测样本的3个邻居在实线的内圆里，按多数投票结果，它属于红色三角形类。但是如果k取5，那么待测样本的最邻近的5个样本在虚线的圆里，按表决法，它又属于蓝色正方形类。在实际应用中，K先取一个比较小的数值，再采用交叉验证法来逐步调整K值，最终选择适合该样本的最优的K值。

• 较小的K值： 优点： 近似误差（approximation error）会减小，只有与输入实例较近的（相似的）训练实例才会对预测结果起作用。 缺点：是“学习”的估计误差（estimation error）会增大，预测结果会对近邻的实例点非常敏感
• 较大的K值： 优点是可以减少学习的估计误差。 但缺点是学习的近似误差会增大。这时与输入实例较远的（不相似的）训练实例也会对预测起作用。

在sklearn库中，k值缺省为5.

距离计算

1. 一般使用欧氏距离 (两点的 各维度坐标差 平方和 再开根)
2. 也可使用其他距离，如：曼哈顿距离 （ 两点的 各维度坐标差 绝对值之和 ）
3. 更一般的是 Lp 距离 （Minkowski距离）

KNN缺陷

1. 容易误判：该算法在分类时有个重要的不足是，当样本不平衡时，即：一个类的样本容量很大，而其他类样本数量很小时，很有可能导致当输入一个未知样本时，该样本的K个邻居中大数量类的样本占多数。 但是这类样本并不接近目标样本，而数量小的这类样本很靠近目标样本。
   

2. 计算量大：每一个待分类的样本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。
   改进： KNN算法的改进方法之一是分组快速搜索近邻法。其基本思想是：将样本集按近邻关系分解成组，给出每组质心的位置，以质心作为代表点，和未知样本计算距离，选出距离最近的一个或若干个组，再在组的范围内应用一般的KNN算法。
   由于并不是将未知样本与所有样本计算距离，故该改进算法可以减少计算量，但并不能减少存储量。

KNN计算量优化：KD树（K-dimension tree）

kd树(K-dimension tree)是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是是一种二叉树，表示对k维空间的一个划分，构造kd树相当于不断地用垂直于坐标轴的超平面将K维空间切分，构成一系列的K维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。

使用二分查找法构建平衡KD tree。

输入：k维空间数据集T={x1,x2,...,xN}，其中xi=(x(1)i,x(2)i,...,x(k)i),i=1,2,...,N;
输出：kd树

（1）开始：构造根结点，根结点对应于包含T的k维空间的超矩形区域。选择x(1) 为坐标轴，以T中所有实例的x(1)坐标的中位数为切分点，将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴x(1)垂直的超平面实现。由根结点生成深度为1的左、右子结点：左子结点对应坐标x(1)小于切分点的子区域，右子结点对应于坐标x(1) 大于切分点的子区域。将落在切分超平面上的实例点保存在根结点。

（2）重复。对深度为j的结点，选择x(l)为切分的坐标轴，l=j%k+1，以该结点的区域中所有实例的x(l)坐标的中位数为切分点，将该结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴x(l)垂直的超平面实现。由该结点生成深度为j+1的左、右子结点：左子结点对应坐标x(l)小于切分点的子区域，右子结点对应坐标x(l)大于切分点的子区域。将落在切分超平面上的实例点保存在该结点。

　例. 给定一个二维空间数据集：T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}，构造一个平衡kd树。
　解：根结点对应包含数据集T的矩形，选择x(1)轴，6个数据点的x(1)坐标中位数是6，这里选最接近的(7,2)点，以平面x(1)=7将空间分为左、右两个子矩形（子结点）；接着左矩形以x(2)=4分为两个子矩形（左矩形中{(2,3),(5,4),(4,7)}点的x(2)坐标中位数正好为4），右矩形以x(2)=6分为两个子矩形，如此递归，最后得到如下图所示的特征空间划分和kd树。

搜索kd树

利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。下面以搜索最近邻点为例加以叙述：给定一个目标点，搜索其最近邻，首先找到包含目标点的叶节点；然后从该叶结点出发，依次回退到父结点；不断查找与目标点最近邻的结点，当确定不可能存在更近的结点时终止。这样搜索就被限制在空间的局部区域上，效率大为提高。

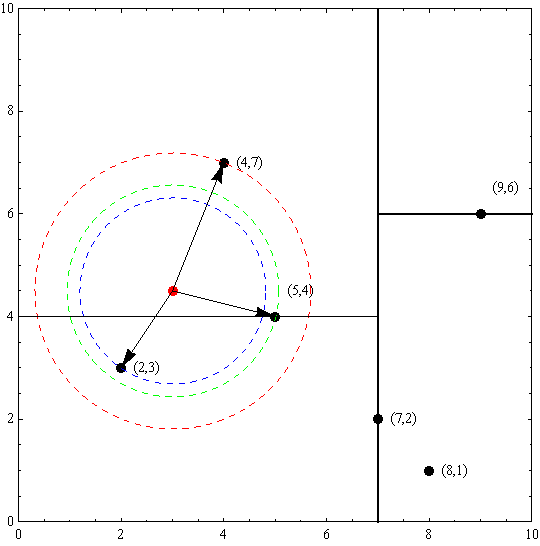
以先前构建好的kd树为例，查找目标点（3,4.5）的最近邻点。同样先进行二叉查找，先从（7,2）查找到（5,4）节点，在进行查找时是由y = 4为分割超平面的，由于查找点为y值为4.5，因此进入右子空间查找到（4,7），形成搜索路径：（7,2）→（5,4）→（4,7），取（4,7）为当前最近邻点。以目标查找点为圆心，目标查找点到当前最近点的距离2.69为半径确定一个红色的圆。然后回溯到（5,4），计算其与查找点之间的距离为2.06，则该结点比当前最近点距目标点更近，以(5,4)为当前最近点。用同样的方法再次确定一个绿色的圆，可见该圆和y = 4超平面相交，所以需要进入（5,4）结点的另一个子空间进行查找。（2,3）结点与目标点距离为1.8，比当前最近点要更近，所以最近邻点更新为（2，3），最近距离更新为1.8，同样可以确定一个蓝色的圆。接着根据规则回退到根结点(7,2)，蓝色圆与x=7的超平面不相交，因此不用进入（7,2）的右子空间进行查找。至此，搜索路径回溯完，返回最近邻点（2,3），最近距离1.8。

reference:

1. KNN算法与Kd树
2. KNN之KD树实现
3. k-d tree算法原理及实现
4. 《统计学习方法》 李航 第3章 k近邻法