Drazil is a monkey. He lives in a circular park. There are n trees around the park. The distance between the i-th tree and (i + 1)-st trees is di, the distance between the n-th tree and the first tree is dn. The height of the i-th tree is hi.
Drazil starts each day with the morning run. The morning run consists of the following steps:
- Drazil chooses two different trees
- He starts with climbing up the first tree
- Then he climbs down the first tree, runs around the park (in one of two possible directions) to the second tree, and climbs on it
- Then he finally climbs down the second tree.
But there are always children playing around some consecutive trees. Drazil can't stand children, so he can't choose the trees close to children. He even can't stay close to those trees.
If the two trees Drazil chooses are x-th and y-th, we can estimate the energy the morning run takes to him as 2(hx + hy) + dist(x, y). Since there are children on exactly one of two arcs connecting x and y, the distance dist(x, y) between trees x and y is uniquely defined.
Now, you know that on the i-th day children play between ai-th
tree and bi-th
tree. More formally, if ai ≤ bi,
children play around the trees with indices from range [ai, bi],
otherwise they play around the trees with indices from 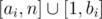 .
.
Please help Drazil to determine which two trees he should choose in order to consume the most energy (since he wants to become fit and cool-looking monkey) and report the resulting amount of energy for each day.
The first line contains two integer n and m (3 ≤ n ≤ 105, 1 ≤ m ≤ 105), denoting number of trees and number of days, respectively.
The second line contains n integers d1, d2, ..., dn (1 ≤ di ≤ 109), the distances between consecutive trees.
The third line contains n integers h1, h2, ..., hn (1 ≤ hi ≤ 109), the heights of trees.
Each of following m lines contains two integers ai and bi (1 ≤ ai, bi ≤ n) describing each new day. There are always at least two different trees Drazil can choose that are not affected by children.
For each day print the answer in a separate line.
5 3 2 2 2 2 2 3 5 2 1 4 1 3 2 2 4 5
12 16 18
3 3 5 1 4 5 1 4 3 3 2 2 1 1
17 22
11
这题是看题解才做出来的,学了怎么用地址符处理函数。这题的思路先是把环变成长度为2*n的链,后面长度n相当于用前面的n补齐.题目要求算的是最大消耗的能量,即sum(x,y)=2*h[x]+2*h[y]+d[y-1]-d[x-1](x<y,注意x!=y,因为是两棵树),这里变形一下,可以得到sum(x,y)=2*h[x]+2*h[y]+d[1]+d[2]+...+d[y-1]-d[1]-d[2]-...-d[x-1],我们记a=2*h[y]+d[1]+d[2]+...+d[y-1],b=2*h[x]-d[1]-d[2]-...-d[y-1],那么我们要求的sum(x,y)就是a+b的最大值,但是这里有个地方要注意,a和b取到最大值的时候可能x==y,即同一棵树,这样就错了。这里我想了很久,最后想通了,= =。
我们可以用区间合并的方法,每次合并的必须是不同的子区间,那么就不可能会发生相等的情况。
<pre name="code" class="cpp">#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<string>
#include<algorithm>
using namespace std;
#define maxn 100500
#define inf 100000000000000
#define ll __int64
ll h[2*maxn],d[2*maxn];
struct node1{
ll l,r;
ll maxa,maxb,maxcha;
}b[8*maxn];
struct node{
ll maxa,maxb,maxcha;
};
void build(ll l,ll r,ll i)
{
ll mid;
b[i].l=l;b[i].r=r;
if(l==r){
b[i].maxa=2*h[l]+d[l-1];
b[i].maxb=2*h[l]-d[l-1];
b[i].maxcha=-inf;
return;
}
mid=(l+r)/2;
if(r<=mid)build(l,r,i*2);
else if(l>mid)build(l,r,i*2+1);
else{
build(l,mid,i*2);
build(mid+1,r,i*2+1);
}
b[i].maxcha=max(b[i*2].maxcha,b[i*2+1].maxcha);
b[i].maxcha=max(b[i].maxcha,b[i*2+1].maxa+b[i*2].maxb );
b[i].maxa=max(b[i*2].maxa,b[i*2+1].maxa);
b[i].maxb=max(b[i*2].maxb,b[i*2+1].maxb);
}
node question(ll l,ll r,ll i)
{
ll mid;
if(b[i].l==l && b[i].r==r){
node temp;
temp.maxa=b[i].maxa;
temp.maxb=b[i].maxb;
temp.maxcha=b[i].maxcha;
return temp;
}
mid=(b[i].l+b[i].r)/2;
if(r<=mid)return question(l,r,i*2);
else if(l>mid)return question(l,r,i*2+1);
else{
node temp,temp1,temp2;
temp1=question(l,mid,i*2);
temp2=question(mid+1,r,i*2+1);
temp.maxcha=max(temp1.maxcha,temp2.maxcha);
temp.maxcha=max(temp.maxcha,temp2.maxa+temp1.maxb);
temp.maxa=max(temp1.maxa,temp2.maxa);
temp.maxb=max(temp1.maxb,temp2.maxb);
return temp;
}
}
int main()
{
ll n,m,i,j,e,c;
while(scanf("%I64d%I64d",&n,&m)!=EOF)
{
for(i=1;i<=n;i++){
scanf("%I64d",&d[i]);
}
for(i=1;i<=n;i++){
scanf("%I64d",&h[i]);
}
for(i=n+1;i<=2*n;i++){
d[i]=d[i-n];
h[i]=h[i-n];
}
for(i=2;i<=2*n;i++){
d[i]=d[i-1]+d[i];
}
build(1,2*n,1);
for(i=1;i<=m;i++){
scanf("%I64d%I64d",&c,&e);
c--;e++;
if(e<c){
node temp;
temp=question(e,c,1);
printf("%I64d
",temp.maxcha);
}
else{
node temp;
temp=question(e,c+n,1);
printf("%I64d
",temp.maxcha);
}
}
}
return 0;
}