2115: [Wc2011] Xor
Time Limit: 10 Sec Memory Limit: 259 MB
Submit: 5714 Solved: 2420
题目链接:https://www.lydsy.com/JudgeOnline/problem.php?id=2115
Description:

Input:
第一行包含两个整数N和 M, 表示该无向图中点的数目与边的数目。 接下来M 行描述 M 条边,每行三个整数Si,Ti ,Di,表示 Si 与Ti之间存在 一条权值为 Di的无向边。 图中可能有重边或自环。
Output:
仅包含一个整数,表示最大的XOR和(十进制结果),注意输出后加换行回车。
Sample Input:
1 2 2
1 3 2
2 4 1
2 5 1
4 5 3
5 3 4
4 3 2
Sample Output:
6
Hint:
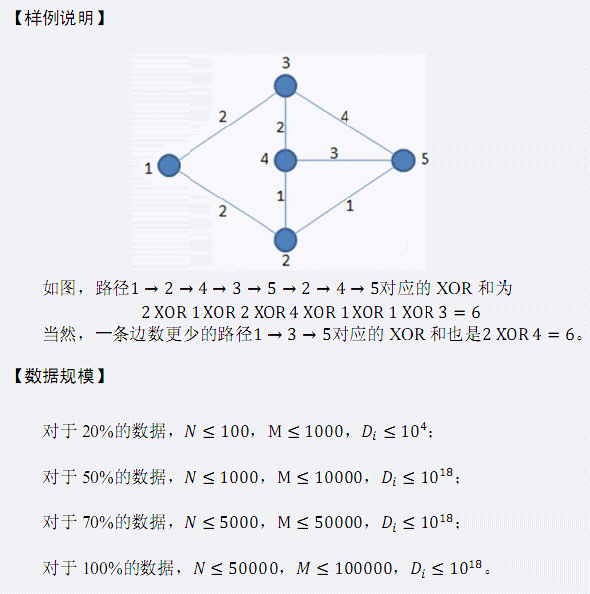
题解:
我感觉这个题是很巧妙的一个题,直接dfs搜路径是显然行不通的。
其实通过观察可以发现,最终的最大异或值所走的路径,一定是一条路径加上若干环形成的。
那么我们考虑通过一次dfs将所有环的异或和求出来,然后随便选择一条路径作为我们的起始路径,这里有两种情况:
1.环没在路径上,那么此时我们走的时候就是通过若干点到那个环,然后又从那若干点回来,最终对答案有贡献的就只有环的异或和;
2.环在路径上,此时我们将这个环与原路径异或一下,那么原路径与环重叠部分就会抵消,然后会形成一条新的更优的路径。
那么此时如果我们将环与路径的最大异或值找出来,最终也是一条路径和若干环,这时就考虑利用线性基来求异或最大值。
代码如下:
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 100005,M = 100005; int n,m,tot,num; int head[N],vis[N]; ll x[N],cir[N<<1]; struct Edge{ int u,v,next; ll w; }e[M<<1]; void adde(int u,int v,ll w){ e[tot].v=v;e[tot].next=head[u];e[tot].w=w;head[u]=tot++; } void dfs(int u,int fa){ vis[u]=1; for(int i=head[u];i!=-1;i=e[i].next){ int v=e[i].v; if(v==fa) continue ; if(!vis[v]){ x[v]=x[u]^e[i].w; dfs(v,u); }else{ cir[++num]=x[v]^x[u]^e[i].w; } } } ll p[65]; ll ans; void xor_base(){ for(int i=1;i<=num;i++){ for(ll j=62;j>=0;j--){ if((1LL<<j)&cir[i]){ if(!p[j]){ p[j]=cir[i]; break; } cir[i]^=p[j]; } } } } int main(){ ios::sync_with_stdio(false);cin.tie(0); cin>>n>>m; memset(head,-1,sizeof(head));tot=num=0; for(int i=1;i<=m;i++){ int u,v;ll w; cin>>u>>v>>w; adde(u,v,w);adde(v,u,w); } dfs(1,-1); ans=x[n]; xor_base(); for(int i=62;i>=0;i--){ ans=max(ans,ans^p[i]); } cout<<ans; return 0; }