Educational Codeforces Round 85 (Rated for Div. 2)

传送门

A. Level Statistics

签到。

Code

/*
 * Author:  heyuhhh
 * Created Time:  2020/4/10 22:41:10
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 100 + 5;
 
int n;
int p[N], c[N];
 
void run() {    
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> p[i] >> c[i];
    for(int i = 1; i <= n; i++) {
        if(p[i] < p[i - 1] || c[i] < c[i - 1]) {
            cout << "NO" << '
';
            return;
        }   
        if(p[i] < c[i]) {
            cout << "NO" << '
';
            return;   
        }
        if(p[i] - p[i - 1] < c[i] - c[i - 1]) {
            cout << "NO" << '
';
            return;   
        }
    }
    cout << "YES" << '
';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    int T; cin >> T; 
    while(T--) run();
    return 0;
}

B. Middle Class

贪心。排序后求出前缀和直接搞即可。

Code

/*
 * Author:  heyuhhh
 * Created Time:  2020/4/10 22:48:39
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
 
int n, x;
int a[N];
ll sum[N];
 
void run() {
    cin >> n >> x;
    for(int i = 1; i <= n; i++) cin >> a[i];
    sort(a + 1, a + n + 1);
    reverse(a + 1, a + n + 1);
    for(int i = 1; i <= n; i++) sum[i] = sum[i - 1] + a[i];
    int ans = 0;
    for(int i = 1; i <= n; i++) {
        if(1ll * x * i <= sum[i]) ans = i;   
    }
    cout << ans << '
';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    int T; cin >> T; 
    while(T--) run();
    return 0;
}

C. Circle of Monsters

题意：
现有(n)只怪兽围成环，每个怪兽有两个属性(a_i,b_i)，(a_i)为其生命值，(b_i)为怪兽死亡后对下一个怪兽造成的伤害。
现在你每次可以打一发子弹使得一个怪兽生命减(1)，问最少需要打多少子弹，使得所有怪兽都死亡。

思路：
如果是一条链的话，那直接从第一个怪兽开始打，所需要的最少子弹数都是不变的。
但题目中是一个环，我们可以直接枚举起点，然后就会在某个地方断开变为一条链。因为链的情况答案不会发生改变，提前通过前缀和计算即可。
详见代码：

Code

/*
 * Author:  heyuhhh
 * Created Time:  2020/4/11 0:04:38
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 6e5 + 5;
 
int n;
ll a[N], b[N], sum[N];
 
void run() {
    cin >> n;
    for(int i = 1; i <= n; i++) {
        cin >> a[i] >> b[i];
        a[i + n] = a[i], b[i + n] = b[i];
    }
    for(int i = 1; i <= 2 * n; i++) sum[i] = sum[i - 1] + max(0ll, a[i] - b[i - 1]);
    ll ans = 1e18;
    for(int i = 1; i <= n; i++) {
        ll res = a[i] + sum[i + n - 1] - sum[i];
        ans = min(ans, res);
    }
    cout << ans << '
';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    int T; cin >> T;
    while(T--) run();
    return 0;
}

D. Minimum Euler Cycle

就类似于这样走就行：
(1,2,1,3,cdots,1,n,2,3,2,4,cdots,2,n,3,4,cdots,n-1,n,1)
即可。
随便求一下就行。

Code

/*
 * Author:  heyuhhh
 * Created Time:  2020/4/15 8:39:21
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
 
ll n, l, r;
 
ll f[N];
void init() {
    for(int i = 1; i <= n; i++) {
        f[i] = f[i - 1] + 2 * (n - i);
    }
}
 
int calc(ll i) {
    if(i == f[n] + 1) return 1;
    int t = lower_bound(f + 1, f + n + 1, i) - f - 1;
    i -= f[t];
    if(i & 1) return t + 1;
    else return i / 2 + t + 1;
}
 
void run() {
    cin >> n >> l >> r;
    init();
    for(ll i = l; i <= r; i++) {
        cout << calc(i) << " 
"[i == r];   
    }
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    int T; cin >> T;
    while(T--) run();
    return 0;
}

E. Divisor Paths

题意：
给出整数(D,Dleq 10^{16})，现在由(D)的所有因子按照如下规则构造一张图：

• 对于两个因子(u,v)，若(u|v且v/u=p,p)为一个素数，那么(u,v)之间存在一条边；
• 边((u,v))的边权为整除(u)但不整除(v)的因子个数。

类似于下图：

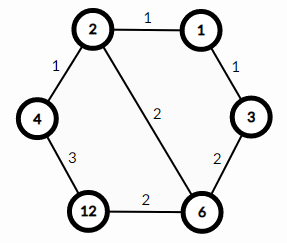
现在给出多组询问，对于每组询问((u,v))，回答从(u)到(v)最短路径有多少条。

思路：
这种数学题，我们一点一点来剖析其性质。

• 对于一条边((u,v),u<v)，其边权为(d(v)-d(u))，其中(d(i))为(i)的因子个数。

那么对于一条路径而言，长度只于起点和终点两点有关。
我们现在要从(x)走到(y,x>y)，路径长度为(d(x)-d(y))。

• 我们可以将该图形抽象为(k)维网格图，每次只能在某一维度走一步，每一维代表一个素因子。

据此我们可以得出从(x)到(y)的最优的走法：(x ightarrow gcd(x,y) ightarrow y)或者(x ightarrow lcm(x,y) ightarrow y)。
接下来就证明第一种走法比第二种走法更优。
我们记(g=gcd(x,y),l=lcm(x,y))，那么两种的贡献分别为：(d(x)+d(y)-d(g)-d(g),d(l)+d(l)-d(x)-d(y))，我们将两者相减：

[egin{aligned} &2(d(x)+d(y)-d(g)-d(l))\\ =&2d(g)(d(frac{x}{g})+d(frac{y}{g}) - 1-d(frac{l}{g})) end{aligned} ]

这里我们应该还是比较容易发现等式是小于等于(0)的，感觉就是证明(d(a)+d(b)-1leq d(ab)=d(a)cdot d(b),a,b)互质。
所以我们就证明了最优走法。
也有另外一种证明方法：因为是网格图，假设为二维网格图，我们要从(xy ightarrow (x-1)(y+1))，那么有两种走法，通过简单比较就会发现肯定先往小的走再往大的走更优，然后就没了。
我们事先在(O(sqrt{n}))的时间复杂度内找到所有(D)的素因子，然后对于每个询问直接搞就行。
代码如下：

Code

/*
 * Author:  heyuhhh
 * Created Time:  2020/4/15 18:59:20
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <numeric>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5, MOD = 998244353;
 
int qpow(ll a, ll b) {
    ll res = 1;
    while(b) {
        if(b & 1) res = res * a % MOD;
        a = a * a % MOD;
        b >>= 1;
    }
    return res;
}
 
void run() {
    ll D; cin >> D;
    vector <ll> primes;
    for(ll i = 2; i * i <= D; i++) if(D % i == 0) {
        primes.push_back(i);
        while(D % i == 0) D /= i;
    }
    if(D > 1) primes.push_back(D);
    vector <ll> fac(100), inv(100);
    fac[0] = 1;
    for(int i = 1; i < 100; i++) fac[i] = fac[i - 1] * i % MOD;
    inv[99] = qpow(fac[99], MOD - 2);
    for(int i = 98; i >= 0; i--) inv[i] = inv[i + 1] * (i + 1) % MOD;
    auto calc = [&](ll x, ll y) {
        vector <ll> v;
        for(auto it : primes) if(x % it == 0) {
            int cnt = 0;
            while(x % it == 0) {
                if(y % it == 0) {
                    x /= it, y /= it;
                } else {
                    x /= it;
                    ++cnt;   
                }
            }
            v.push_back(cnt);
        }          
        ll res = fac[accumulate(all(v), 0)];
        for(auto it : v) res = res * inv[it] % MOD;
        return res;
    };
    int q; cin >> q;
    while(q--) {
        ll a, b; cin >> a >> b;
        ll g = __gcd(a, b);
        ll ans = calc(a, g) * calc(b, g) % MOD;
        cout << ans << '
';
    }
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    run();
    return 0;
}

F. Strange Function

题意：
给出序列(a_{1,2,...,n})，现在定义(f(a))表示选择所有(i)，满足(a_i>max{a_j},j<i)的(a_i)出来，得到一个递增的序列(b)。
现在可以删除某些位置上的数花费(p_i)的代价（可以为负）。
现在给出(b)，问最少要多少代价，使得(f(a)=b)。

思路：
定义(dp_{i,j})表示现在位于(a)序列第(i)位，(b)序列第(j)位的最小代价，我们考虑下一个位置(a_{i+1}:)

• 假设(a_{i+1}leq b_j)，我们可以删除或者不删除，此时(dp_{i+1,j}=dp_{i,j}+min(0,p_{i+1}))；
• 假设(a_{i+1}>b_j)，此时又分两种情况：
  • 若(a_{i+1}=b_{j+1})，那么此时可选可不选，所以就有(dp_{i+1,j}=dp_{i,j}+p_{i+1},dp_{i+1,j+1}=dp_{i,j});
  • 若(a_{i+1} ot ={b_{j+1}})，此时我们必须删除，那么(dp_{i+1,j}=dp_{i,j}+p_{i+1})。

我们相当于有三种转移，因为(b)数组是连续的，并且我们观察到转移时只有一种情况是(j)向(j+1)转移的。
我们可以用线段树维护所有(dp_{i-1,j})的值，然后我们将(b)分为几个区间，分别按照转移方程进行区间/单点修改即可。
很巧妙的一个题，主要利用了转移方程(j)不变以及(b)单调的性质，因此我们可以沿用之前的状态并且分区间进行区间修改。
细节见代码：

Code

/*
 * Author:  heyuhhh
 * Created Time:  2020/4/15 20:23:48
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 5e5 + 5;
 
int n, m;
int a[N], p[N], b[N];
 
ll minv[N << 2], lz[N << 2];
 
void tag(int o, ll v) {
    minv[o] += v, lz[o] += v;
}
 
void push_up(int o) {
    minv[o] = min(minv[o << 1], minv[o << 1|1]);
}
 
void push_down(int o, int l, int r) {
    if(lz[o] != 0) {
        int mid = (l + r) >> 1;
        tag(o << 1, lz[o]);
        tag(o << 1|1, lz[o]);
        lz[o] = 0;   
    }
}
 
void build(int o, int l, int r) {
    lz[o] = 0;
    if(l == r) {
        if(l == 0) minv[o] = 0;
        else minv[o] = 1e18;
        return;
    }
    int mid = (l + r) >> 1;
    build(o << 1, l, mid), build(o << 1|1, mid + 1, r);
    push_up(o);
}
 
void update(int o, int l, int r, int L, int R, ll v) {
    if(L > R) return;
    if(L <= l && r <= R) {
        tag(o, v); return;
    }   
    push_down(o, l, r);
    int mid = (l + r) >> 1;
    if(L <= mid) update(o << 1, l, mid, L, R, v);
    if(R > mid) update(o << 1|1, mid + 1, r, L, R, v);
    push_up(o);
}
 
void modify(int o, int l, int r, int p, ll v) {
    if(l == r) {
        minv[o] = min(minv[o], v);
        return;
    }   
    push_down(o, l, r);
    int mid = (l + r) >> 1;
    if(p <= mid) modify(o << 1, l, mid, p, v);
    else modify(o << 1|1, mid + 1, r, p, v);
    push_up(o);
}
 
ll query(int o, int l, int r, int L, int R) {
    if(L <= l && r <= R) {
        return minv[o];
    }
    push_down(o, l, r);
    int mid = (l + r) >> 1;
    ll res = 1e18;
    if(L <= mid) res = query(o << 1, l, mid, L, R);
    if(R > mid) res = min(res, query(o << 1|1, mid + 1, r, L, R));
    return res;
}
 
void run() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) cin >> p[i];
    cin >> m;
    for (int i = 1; i <= m; i++) cin >> b[i];
    for (int i = 1, j = 1; i <= n; i++) {
        if (a[i] == b[j]) ++j;
        if(i == n && j <= m) {
            cout << "NO" << '
';
            return;   
        }
    }
    build(1, 0, m);
    for (int i = 0; i < n; i++) {
        int t = lower_bound(b + 1, b + m + 1, a[i + 1]) - b;
        if (p[i + 1] < 0) update(1, 0, m, t, m, p[i + 1]);
        if (b[t] == a[i + 1]) {
            ll v = query(1, 0, m, t - 1, t - 1);
            modify(1, 0, m, t, v);
        }
        update(1, 0, m, 0, t - 1, p[i + 1]);
    }
    ll ans = query(1, 0, m, m, m);
    cout << "YES" << '
';
    cout << ans << '
';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    run();
    return 0;
}

G. Substring Search

题意：
给出(s)串和(t)串，现在问对于(s)的每个长度为(m)的子串，是否有(s'=t)。字符串相等定义为：

• 对于(1leq ileq len,s_i=t_i或p_{s_i}=t_i);

其中(p)为(1)到(26)的排列。
对所有的(1leq ileq n-m+1)都要输出答案。

思路：
将字符串相等形式化即可表示为：

[sum_{i=0}^{n-m-1}sum_{j=0}^{m-1}(t_j-s_{i+j})^2cdot (t_j-p_{s_{i+j}})^2=0 ]

那么稍微变一下即为：

[sum_{j=0}^{m-1}sum_{i=0}^{n-m-1}(t_j-s_{i+j})^2cdot (t_j-p_{s_{i+j}})^2=0 ]

后面这一部分我们直接将其打开是一个关于(t_j)的四次多项式，系数是关于(i+j)位置的一个表达式。
那么我们直接将多项式拆开算，提前算出来系数，然后对于每一项求卷积即可。
关键在于形式化的表述，这一步挺巧妙的，平方的话是使得其结果非负，那么如果为(0)的话，就说明这个等式即保证了每一项都至少有一个成立。
代码略。