最短路--差分约束

求(a[u]-a[v])的最大值

已知(a[1]-a[2] <= 5)，那么 (a[1]-a[2]) 的最大值就是5
如果(a[3]-a[2] <= 2)，(a[1]-a[3] <= 2)，那么(a[1]-a[2]) 的最大值就是4
翻译一下上面的约束条件，1最多比2大5，3最多比2大2，1最多比3大2
画个图理解一下

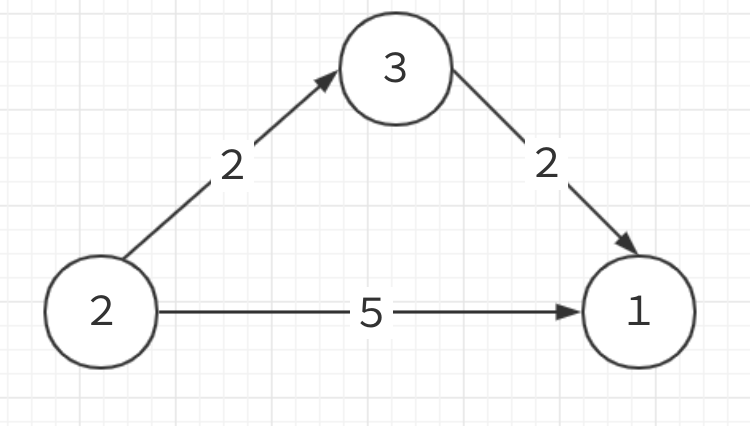
对于每个不等式 (x[i] - x[j] <= a[k])，对结点 j 和 i 建立一条 j -> i的有向边，边权为a[k]
(a[u]-a[v])的最大值就是求v到u的最短路

求(a[u]-a[v])的最小值

已知(a[1]-a[2] >= 5)，那么 (a[1]-a[2]) 的最小值就是5
如果(a[3]-a[2] >= 3)，(a[1]-a[3] >= 6)，那么(a[1]-a[2]) 的最小值就是9
翻译一下上面的约束条件，1最少比2大5，3最少比2大3，1最少比3大6
画个图理解一下

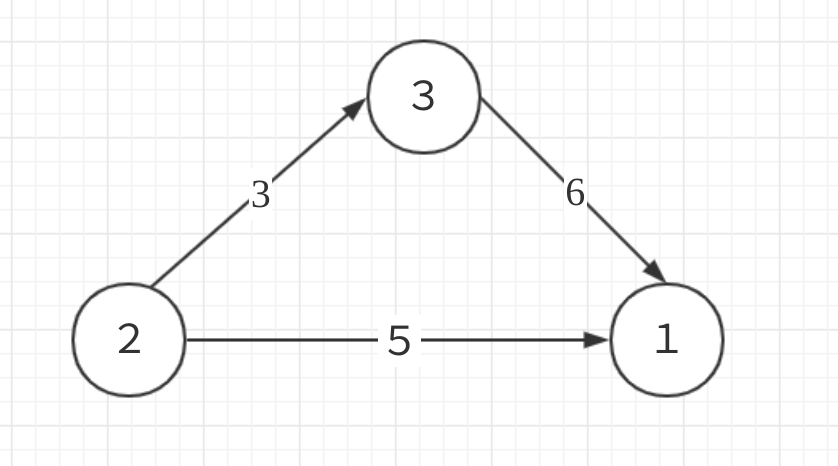
对于每个不等式 (x[i] - x[j] >= a[k])，对结点 j 和 i 建立一条 j -> i的有向边，边权为a[k]
(a[u]-a[v])的最大值就是求v到u的最长路

总结一下

如果是求最大值的话，统一把差分约束改成<=的形式，然后求最短路，小于号就是最短路
如果是求最小值的话，统一把差分约束改成>=的形式，然后求最长路，大于号就是最长路
P5960 【模板】差分约束算法

code

#pragma GCC optimize(2)
#include <bits/stdc++.h>
using namespace std;
#define debug(x) cerr << #x << " : " << x << " " << endl
#define mem(a,b) memset(a,b,sizeof(a))
#define pii pair<int,int>
#define gcd __gcd
const int inf = 0x3f3f3f3f;
const int maxn = 201110;
const int M = 1e9+7;
int n,m,k,ok;

int head[maxn],cost[maxn],to[maxn],Next[maxn],cnt = 2;

void add(int u,int v,int w)
{
    to[cnt] = v;cost[cnt] = w;Next[cnt] = head[u];head[u] = cnt;cnt++;
}

int in[maxn];
bool vis[maxn];
int dis[maxn];

bool spfa(int u)            //spfa求最短路
{   
    mem(dis,inf);dis[u] = 0;
    queue<int> q;q.push(u);
    while (!q.empty())
    {
        u = q.front();q.pop();vis[u] = 0;
        for(int i = head[u]; i ; i = Next[i])
        {
            int v = to[i];
            if(dis[v] > dis[u]+cost[i])        //求最长路把这里改成大于就好了
            {   
                dis[v] = dis[u]+cost[i];
                if(!vis[v])
                {
                    vis[v] = 1;
                    q.push(v);
                    in[v]++;
                    if(in[v] == n+1) return false;            //出现负环,如果是求最长路就是出现正换
                }
            }
        }
    }
    return true;
}

signed main()
{
    cin>>n>>m;
    for(int i = 1; i <= n; i++)         //确保联通,构建超级源点
    {
        add(n+1,i,0);
    }
    for(int i = 1,u,v,w; i <= m; i++) 
    {
        cin>>u>>v>>w;
        add(v,u,w);
    }
    if(spfa(n+1))
    {
        for(int i = 1; i <= n; i++) 
        {
            cout<<dis[i]<<' ';
        }
        cout<<endl;
    }
    else puts("NO");
    return 0;
}

参考博客

https://www.cnblogs.com/zzz-hhh/p/11200893.html#664675501