线段特征上的扫描点满足 (1)。本文的线段特征定义为:L: [dL, φL, PLs, PLe]T,如图1所示。其中,dL为笛卡尔坐标系中原点(激光传感器所在位置)到线段的距离, φL为线段特征的倾角,PLs为线段特征起点,PLe为线段特征终点。线段特征在笛卡尔坐标系下方程为:
 (1)
(1)
其中,dL > 0,-π < φL < π,xi = ρicosφi,yi = ρisinφi。
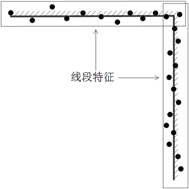
图1 线段
前几节中,通过统计学方法划分出若干区域,为了准确提取线段特征,采用带约束的最小二乘法对每个划分区域特征进行特征提取,将(1)式转换为如下形式:
 (2)
(2)
式中 S、E——线段端点。
将上式改写为矩阵形式有:
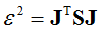 (3)
(3)
其中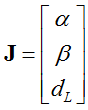 ,
,  ,
,  ,
,  。由于α2+β2=1,引入拉格朗日乘子λ,得:
。由于α2+β2=1,引入拉格朗日乘子λ,得:
 (4)
(4)
其中,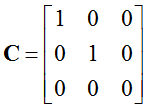 ,满足JTCJ=1。令
,满足JTCJ=1。令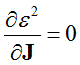 ,得:
,得:
 (5)
(5)
解上式的广义特征值与广义特征向量,S为一个正定矩阵,待求特征向量J一定对应最小的特征值λ。当α与β确定以后,可以求得:
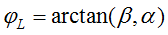 (6)
(6)
然后,求出线段特征dL。最后,转换到全局坐标系下。
文献[1]给出了一种误差传播方法,通过最小化隐含的关系方程F(I,O),给出最终误差(I输入误差,O输出误差)。将误差扩展到协方差矩阵,可以通过输入的协方差矩阵ΣI,得到输出的协方差矩阵ΣL。则有:
 (7)
(7)
其中, 。
。 ,
,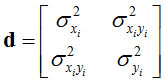 令:
令:
 (8)
(8)
代入最后计算出ΣL。
[1] Haralick R M. Propagating covariance in computer vision[M]. Performance Characterization in Computer Vision. Springer Netherlands, 2000: 95-114.