首先说明这篇博客写得奇差无比
让我们理清一下为什么要打分块,在大部分情况下,线段树啊,splay,treap,主席树什么的都要比分块的效率高得多,但是在出问题的时候如果你和这些数据结构只是混的脸熟的话,一旦错误可能就会导致心态崩溃,而且调试困难(大佬:很轻松啊....)所以,分块是一个时间效率不是很高的,代码量也不是很高的数据结构,水分是可以的,在全场都是30分的情况下,你能用分块水到个60,70就是胜利,所以分块很多时候也是和STL一起用的,达到(nlogn√n)的效果吧。
原理
把一段数列1...n分成√n块,如果√n*√n<n,√n++。这样能保证每一块的大小都<=√n,我不会证明,但是此时时间复杂度一般为(n√n),就可以开始水分了。
比如,在我们要解决一段100000左右的序列时,最简单的询问 (l,r)求和 给(l,r)加上一个值。
大佬A:线段树@#@@¥%@!#(啪)
大佬B:平衡树%¥……¥#%@@(啪)
大佬C:树套树@¥%@#%#……(啪)
那么身为蒟蒻的我:分块!(瑟瑟发抖)
首先让我们来讲一讲分块是什么
分块,我这里只是简单的把一段数,放到几个块里面,怎么放呢,按照某个大佬的证明,把每连续的√n个数放在一个块里的时间复杂度一般是最优的,当然有时候√n并不是最优解。
那么要怎么分呢?
首先,我们让int tmp=sqrt(当前有多少个数),这样就可以保证有√n块。
然后如果有任何一块处于(l,r)之间,就给这个块打上标记进行操作。
这样肯定是有可能会有 l和r 处在两个块中的,而且我们也不能对那两的块直接修改。
就暴力修改块里面的内容。即每一次的时间复杂度大概为(3√n)。
所以我们就是要预先处理好每一块的内容,预处理大概是(n√n)的,查询大概是(1)的。
让我们来看这样一道问题
题目背景
此题约为NOIP提高组Day2T2难度。
题目描述
众所周知,模数的hash会产生冲突。例如,如果模的数p=7,那么4和11便冲突了。
B君对hash冲突很感兴趣。他会给出一个正整数序列value[]。
自然,B君会把这些数据存进hash池。第value[k]会被存进(k%p)这个池。这样就能造成很多冲突。
B君会给定许多个p和x,询问在模p时,x这个池内数的总和。
另外,B君会随时更改value[k]。每次更改立即生效。
保证1<=p<n1<=p<n1<=p<n .
输入输出格式
输入格式:
第一行,两个正整数n,m,其中n代表序列长度,m代表B君的操作次数。
第一行,n个正整数,代表初始序列。
接下来m行,首先是一个字符cmd,然后是两个整数x,y。
-
若
cmd='A',则询问在模x时,y池内数的总和。 -
若
cmd='C',则将value[x]修改为y。
输出格式:
对于每个询问输出一个正整数,进行回答。
输入输出样例
输入样例#1:
10 5
1 2 3 4 5 6 7 8 9 10
A 2 1
C 1 20
A 3 1
C 5 1
A 5 0
输出样例#1:
25
41
11
说明
样例解释
A 2 1的答案是1+3+5+7+9=25.
A 3 1的答案是20+4+7+10=41.
A 5 0的答案是1+10=11.
数据规模
对于10%的数据,有n<=1000,m<=1000.
对于60%的数据,有n<=100000.m<=100000.
对于100%的数据,有n<=150000,m<=150000.
保证所有数据合法,且1<=value[i]<=1000.
注:以下引至大佬阮行止的讲解
这是一道论文题。集训队论文《根号算法——不只是分块》。
首先,题目要我们求的东西,就是下面的代码:
for(i=k;i<=n;i+=p)
ans+=value[i];
即:从 k开始,每隔p个数取一个数,求它们的和。
这个算法的复杂度是 (O(n^2)) 的。
令答案为 (ans[p][k]) ,表示模数是p,余数是k.
那么,对于第(i)个数,如何处理它对(ans)的贡献呢?
for(p=1;p<=n;p++) //枚举模数
ans[p][i%p]+=value[i]; //处理对应的贡献
这样看上去很妙的样子,然而 (O(n^2)) 的预处理, (O(1)) 询问,空间复杂度还是
(O(n^2)) 的
所以我们很自然地想到:只处理 ([1,sqrt{n}]) 以内的p
这样的话,令 (size=sqrt{n}) ,则可以这样预处理:
for(p=1;p<=size;p++) //只枚举[1,size]中的
ans[p][i%p]+=value[] //处理对应的贡献
于是预处理的复杂度降到了 (O(nsqrt{n})) .
接着考虑询问。如果询问的(p<size) ,那显然可以 (O(1)) 给出回答。
如果p超过size,我们就暴力统计并回答。因为 (p>sqrt{n}) ,所以少于 (sqrt{n}) 个数对答案有贡献。所以对于 (p>sqrt{n}) ,暴力统计的复杂度是 (O(sqrt{n})) ..
接着考虑修改。显然我们把p<size的值全都更新一遍就行。复杂度也是 (O(sqrt{n})) .
void change(int i,int v) //将value[i]改为v
{
for(p=1;p<=size;p++)
ans[p][i%p]=ans[p][i%p]-value[i]+v; //更新答案
value[i]=v; //更新value数组
}
这样,我们就在 (O((m+n)sqrt{n})) .的时间内完成了任务
这便是分块的思想。
也许我们要结合图来说明一下

然后当我遍历一段序列时,比如我要给第4至18加上一个数,那么分块的实现就是第一块(因为只涉及到一部分)的4,5暴力加上那个数,第四块的16,17,18暴力加上那个数,然后给第(2),(3)块打上一个lazy标记,就和线段树一样
大概的建块过程如下
void build()
{
num=tmp;if(tmp*tmp<n)num++; //因为int向下取整,所以有可能tmp*tmp<n,存不了那么多的数 for(int i=1;i<=num;i++)
{
l[i]=num*(i-1)+1;r[i]=num*i; //每一个块的左右区间
}
r[num]=n; int s=1 ; for (int i=1;i<=n;i++) {if (i>r[s]) s++; belong[i]=s;} //处理出每一个数所属于的块 //... //你要预处理的内容
}
然后查询跟上面也差不多,因题目而异。
下面贴一个静态查询最大值的代码
int query(int x,int y)
{ int ans=-1000000; if(belong[x]==belong[y])//在一个块内就直接暴力统计
{ for(int i=x;i<=y;i++)
ans=max(ans,ch[i]); return ans;
} for(int i=x;i<=r[belong[x]];i++)//统计最左边的块的情况
ans=max(ans,ch[i]); for(int i=belong[x]+1;i<=belong[y]-1;i++)//中间的先于预处理好,然后每一块的情况O(1)查询
ans=max(ans,maxx[i]); for(int i=l[belong[y]];i<=y;i++)//统计最右边的块的情况
ans=max(ans,ch[i]); return ans;
}
所以原理大概就讲到这里吧。
关于做题的分析
分块的题目有很多,并且尽是暴力 毒瘤 题。那么我们要怎么暴力呢?
- 第一种情况,关于分块时,我修改值以后,并不需要修改块内的顺序。
这句话是什么意思呢,就是说,假设,我们当前只需要统计一段区间的和或者xor值等等,那么我们并不需要改变块内数值的顺序,因为块内每个数值的分布,并不会直接影响到我的求和的时间复杂度等等。这简直就是**模版题**。
这一类型的题目一般就是考验你对lazy数组的理解能力,往往就是标记要打对,因为关于块内的遍历询问,就是直接暴力√n的遍历
例题
给出一个长为 nnn 的数列,以及 nnn 个操作,操作涉及区间加法,单点查值。
输入格式
第一行输入一个数字 n。
第二行输入 n 个数字,第 i 个数字为 a_i,以空格隔开。
接下来输入 n 行询问,每行输入四个数字 opt、l、r、c,以空格隔开。
若 opt=0,表示将位于 [l,r] 的之间的数字都加 c。
若 opt=1,表示询问 a_r 的值(l 和 c 忽略)。
输出格式
对于每次询问,输出一行一个数字表示答案。
样例输入
4
1 2 2 3
0 1 3 1
1 0 1 0
0 1 2 2
1 0 2 0
样例输出
2
5
- 第二种情况,关于分块时,我修改值以后,数值的位置会影响结果
这里的结果并不是指会对查询出来的结果有什么影响(目前我做的是这样...),而是对时间复杂度有影响
比如,我要查询一段序列小于等于一个值的数字有多少个,那怎么写呢?(巨老:权值线段树)。
当我们分块完毕时,我们会发现,每个块里面的小于等于一个值的数,我们每次遍历时又不能暴力一个一个去匹配,用一个vis[]数组来统计小于等于的有多少?数值大于1e8你就GG了,何况我们还要一段序列一段序列的修改。
对于此类题目我们就会感觉的到STL的妙处了,先一个sort,把数列排好序,然后vector直接二分啊,log直接找到当前那个值的位置,那个数的前面数(指包含在当前块内的)就是小于等于查询值的嘛,如果块有标记就让查询值先减去lazy值再查询嘛。
虽然每一个块的复杂度不再是O(1)了,当然很舒服的是查询好像只要加上一个log的复杂度,修改是√nlog√n的。
这类题目的实质就是,数值在块内排序后可以二分查找避免暴力,如果是无序的,很明显的就二分查找不了,直接GG,一般都会涉及到STL.
- 第三种问题,关于分块时,我们以大块套小块(前缀和)!
例题
题目描述
神犇SJY虐完HEOI之后给傻×LYD出了一题:
SHY是T国的公主,平时的一大爱好是作诗。
由于时间紧迫,SHY作完诗之后还要虐OI,于是SHY找来一篇长度为N的文章,阅读M次,每次只阅读其中连续的一段[l,r],从这一段中选出一些汉字构成诗。因为SHY喜欢对偶,所以SHY规定最后选出的每个汉字都必须在[l,r]里出现了正偶数次。而且SHY认为选出的汉字的种类数(两个一样的汉字称为同一种)越多越好(为了拿到更多的素材!)。于是SHY请LYD安排选法。
LYD这种傻×当然不会了,于是向你请教……
问题简述:N个数,M组询问,每次问[l,r]中有多少个数出现正偶数次。
输入输出格式
输入第一行三个整数n、c以及m。表示文章字数、汉字的种类数、要选择M次。
第二行有n个整数,每个数Ai在[1, c]间,代表一个编码为Ai的汉字。
接下来m行每行两个整数l和r,设上一个询问的答案为ans(第一个询问时ans=0),令L=(l+ans)mod n+1, R=(r+ans)mod n+1,若L>R,交换L和R,则本次询问为[L,R]。
输出格式:
输出共m行,每行一个整数,第i个数表示SHY第i次能选出的汉字的最多种类数。
输入输出样例
输入样例#1:
5 3 5
1 2 2 3 1
0 4
1 2
2 2
2 3
3 5
输出样例#1:
2
0
0
0
1
说明
对于100%的数据,1<=n,c,m<=10^5
不带修改,直接查询,是不是很舒服?但是正偶数次是不是有点难处理,是的,这道题不是很难但是很难调。
这个思想只是分块里面的一个小小的优化,用一个ans[i][j]保存第i块到第j块内符合条件的数字的个数,o(1)的查询,这种卡常的题目及其恶心。
最后认为自己学好的julao们,把hzwer大佬的分块入门九题写一写,就o**k了
现在我们来讲一些骚操作
块状链表
(我没有打过,很慌)
就是把分块连起来
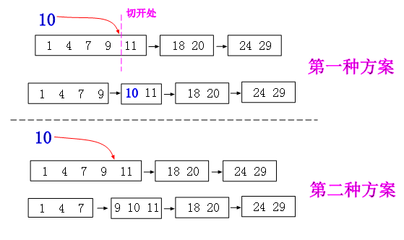
这是插入操作
先暴力加入这个块,当这个块大到影响时间复杂度的时候,我们有两种方法处理
- 从加入处重新断开构成多个块
- 把这两个块加上要插入的一段数暴力重构
至于怎么连接,我们肯定是把每个块用链表结构连起来,
for(int i=1;i<=n;i++)
{
if(bl[i]+1==tmp)continue;
next[bl[i]]=bl[i]+1;
if(bl[i]!=bl[i+1]){
head[bl[i]]=i;
}
}
ps:我也没有写过,不知道对错
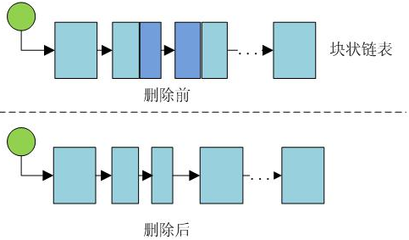
删除同理嘛,设置一个上限参数,当前块内含有的数过少,这样的块如果超过一定数量,就暴力合并。
这个等我没那么菜了以后再完善
树上分块
这是我在树剖里面讲解过的。
例题有两道
[SCOI2005]王室联邦
这一道是告诉我们是怎么去分块的
Description
“余”人国的国王想重新编制他的国家。他想把他的国家划分成若干个省,每个省都由他们王室联邦的一个成
员来管理。他的国家有n个城市,编号为1..n。一些城市之间有道路相连,任意两个不同的城市之间有且仅有一条
直接或间接的道路。为了防止管理太过分散,每个省至少要有B个城市,为了能有效的管理,每个省最多只有3B个
城市。每个省必须有一个省会,这个省会可以位于省内,也可以在该省外。但是该省的任意一个城市到达省会所经
过的道路上的城市(除了最后一个城市,即该省省会)都必须属于该省。一个城市可以作为多个省的省会。聪明的
你快帮帮这个国王吧!
Input
第一行包含两个数N,B(1<=N<=1000, 1 <= B <= N)。接下来N-1行,每行描述一条边,包含两个数,即这
条边连接的两个城市的编号。
Output
如果无法满足国王的要求,输出0。否则输出数K,表示你给出的划分方案中省的个数,编号为1..K。第二行输
出N个数,第I个数表示编号为I的城市属于的省的编号,第三行输出K个数,表示这K个省的省会的城市编号,如果
有多种方案,你可以输出任意一种。
Sample Input
8 2
1 2
2 3
1 8
8 7
8 6
4 6
6 5
Sample Output
3
2 1 1 3 3 3 3 2
2 1 8

直径指两个点之间的距离,指它们之间算上它们有多少个点
每一种题型都有相应的分法,怎么分看julao你。
这一道是真正的练习题:[WC2013]糖果公园