用图像插值来重建关键帧以外的帧。但是用普通的U-Net很难正确地消除moving patterns的轨迹的歧义,因此直接把离线光流估计(来自块运动估计或光流)合并到网络中
新的结构用pre-computed的运动估计来对空间U-net特征进行插值
Preliminary:
(I^{(t)}inmathbb{R}^{W imes R imes 3})表示帧,(t in { 0,1,...})
目标是把帧(I^{(t)})压缩成二进制码(b^{(t)}in {0,1}^{N_t})
Encoder E: (left{I^{(0)}, I^{(1)}, ldots ight} ightarrowleft{b^{(0)}, b^{(1)}, ldots ight})
Decoder D: (left{b^{(0)}, b^{(1)}, ldots ight} ightarrowleft{hat{I}^{(0)}, hat{I}^{(1)}, ldots ight})
Two competing aims:
- 最小化total bitrate (sum_t N_t)
- 尽可能忠实的重建原视频,用(ell (hat{I},I)=| hat{I}-I |_1)来衡量
首先考虑Image Compression:
最简单的Encoder-decoder过程,对每个图像都独立处理,(E_I: I^{(t)} o b^{(t)},;D_I:b^{(t)} o hat{I}^{(t)})
这里以Full resolution image compression with recurrent neural networks中的model为基础,在逐步的超过K次迭代中编码重建图像
每次迭代,模型对previous coded image和original frame间的残差(r_k)进行编码
(g_k)和(h_k)是每次迭代时更新的潜在Conv-LSTM状态
如果(r_0:=I)表示一帧的话
(k=1)时
理解为(r_1)表示原始帧和经过Encoder-Decoder后的图像的残差
那当(k=2)时
(对残差经过Encoder-Decoder之后和原残差的残差?)
训练目标是最小化所有步中的失真distortion (sum_{k=1}^{K} | r_k |_{1})
重建结果为(hat{I}_{K}=sum_{k=1}^{K} D_I (b_k))
选择不同的(K),就会得到不同的二进制编码
Encoder和Decoder包含了4个stride=2的Conv-LSTM,bottleneck由一个L通道,空间分辨率为(frac{1}{16})width( imes frac{1}{16})height的二元特征映射(binary feature map)组成的。
这个结构对image compression来说能达到sota performance,但是它没有利用时间冗余(temporal redundancy),所以用来video compression肯定是不行的
再说到Video Compression,现在的视频编码先用Encoder (E_I)和Decoder (D_I)处理I帧,在P帧中存储块运动估计(mathcal{T}in mathbb{R}^{W imes H imes 2})(类似于光流场),和残差图像(mathcal{R})。运动估计和残差都用熵编码来联合压缩,对图像中的每个像素(i),原始颜色帧(original color frame)用下面的来代替
压缩由块结构和运动估计(mathcal{T})唯一定义,残差就是运动插值后的图像和原图像的差。
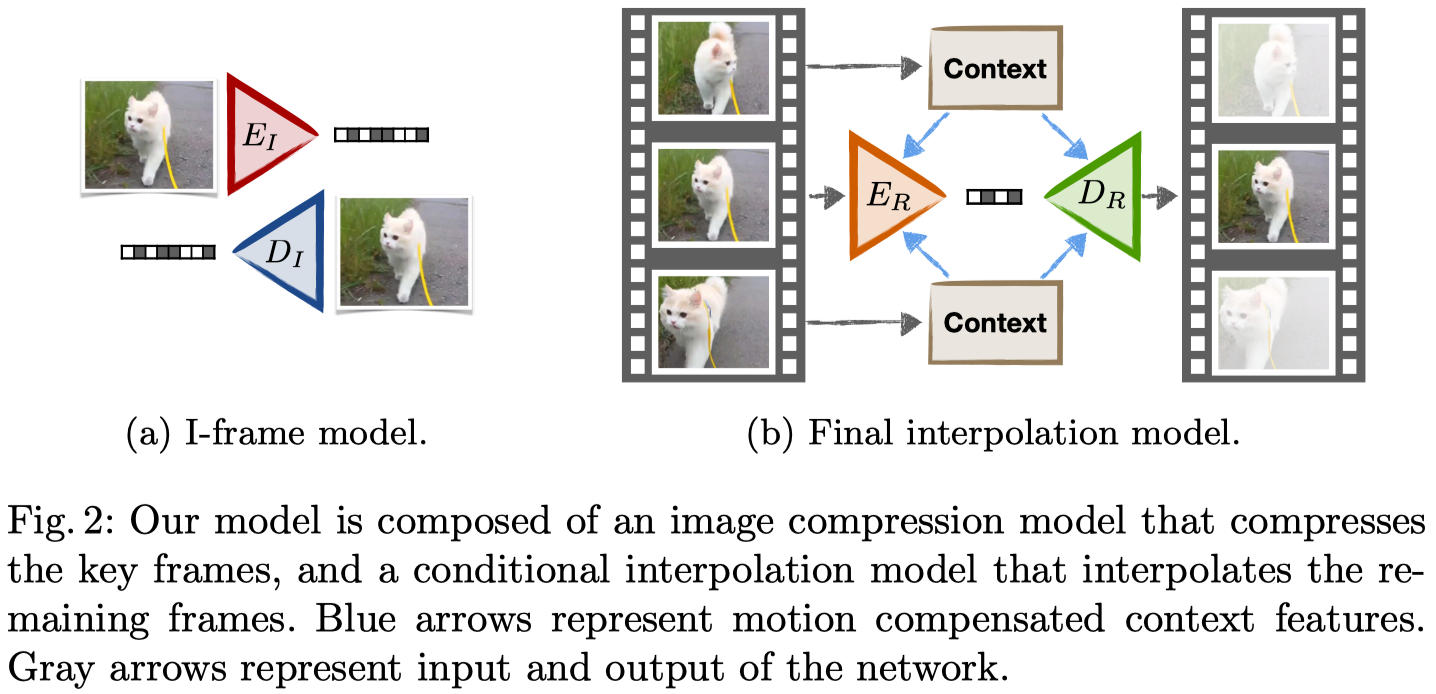
本文就是用图像插值来压缩视频,利用运动信息对图像插值网络进行扩充,增加了可压缩的bottleneck层。
编码解码器首先用Toderici等人的方法(应该指的是这篇?Full resolution image compression with recurrent neural networks,有空再看)来对I帧编码。每隔n帧选一个I帧,剩下的n-1帧通过插值得到,称为R帧。(实际中选n=12)
先来看最简单版本的编码解码器,所有R帧都从关键帧(I_1)和(I_2)中插值得到
训练一个上下文网络(C:I o {f^{(1)},f^{(2)},...})来从不同空间分辨率中提取一系列的特征映射(f^{(l)}),令(f:={f^{(1)},f^{(2)},...})。实现时用U-net结构中的上卷积特征映射(upconvolutional feature maps)在原始图像上增加了(frac{W}{8} imesfrac{H}{8},frac{W}{4} imesfrac{H}{4},frac{W}{2} imesfrac{H}{2},W imes H)这几个空间分辨率
通过这个网络得到关键帧(I_1)和(I_2)的上下文特征(f_1)和(f_2),再训练一个网络D来插值得到帧(hat{I}:=D(f_1,f_2))。C和D是联合训练的
这个最简单的模型可以得到高压缩率,但是得不到很好的图像质量,因为R帧捕捉不到I帧中不存在的信息。光靠I帧来插值,没有更进一步的信息,怎么可能忠实的重建那一帧?
据此,提出了运动补偿插值。就是在网络(?)中加入ground truth motion,定义了像素是从哪里运动过来的。用了光流or块运动估计两种。块运动估计更易压缩,光流的细节更好
也就是说对每个空间位置(i),用运动信息来扭曲每个上下文特征映射
根据feature map的分辨率来缩放运动估计,并对小数点的位置用双线性插值。这样decoder用的就是扭曲的上下文特征( ilde{f})
但是还是只能看见参考图像中的内容,而看不到运动信息之外的信息,目标是将这些剩余的信息尽可能的编码压缩
最终的插值模型称为残差运动补偿插值,结合了运动补偿插值和压缩后的残差信息,这样就又有运动信息,又有插值帧中区别的信息
联合训练:1.encoder (E_R) 2.context model (C) 3.interpolation network (D_R)(Decoder?)
encoder和interpolation network的输入相同,遵循Full resolution image compression with recurrent neural networks中的压缩框架
以扭曲的上下文( ilde{f})作为条件训练一个可变比特率编解码器(variable bitrate encoder and decoder)
插值网络对时间上接近的图像编码需要的比特位较少,较远的需要更多比特位。
所以有两个极端。第一种,关键帧对插值帧没有提供任何有意义的信号,那么算法就变成图像压缩(不插值,就压一下图像)。第二种,图像内容不变,那就是一个最标准的插值,不用编码。
(自己的理解:第一种极端就是插值得到的图像和真实图像差了十万八千里,完全木有关系,那就不编码了,就把真实图像压缩一下。第二种极端就是插值得到的图像就是真实图像,一点没变,那就是普通的插值,不用压缩也就不用编码)
那既然要压缩,肯定希望不用编码只靠插值就能得到的帧越多越好啊,因此文中引出了一个分层插值方案(hierarchical interpolation scheme)
最简单的想法是这样,先插一些帧出来,再把这些帧当成关键帧插下一层的帧,像图里这样

那一层一层往下插,误差肯定越来越大(据说超过三层之后误差就会显著降低性能)
插值模型(mathcal{M}_{a,b}) references a frames into the past and b frames into the future. (这句没看懂什么意思)
对每个时间偏移((a,b)),需要训练一个不同的插值网络(mathcal{M}_{a,b}),因为不同的插值表现不同,而我们还希望能尽可能多的重复相同的时间偏移,这样就可以最大化的重复使用训练模型。此外,最小化时间偏移减少比特率(Q: 为啥?),所以要最小化插值中时间偏移的和。
(Q: 这个temporal offsets到底指的是什么?)
只考虑比特率和插值网络的数量,最优分层方案是二叉树,每层将一个插值范围分成两个。但是这样,因为三层之后误差较大,(n=8)就是极限了
它说我们最后一层的时候,每两个之间插两帧而不是一帧
用的是训练的(mathcal{M}_{1,2})插值模型,对连续四帧(I_1,...,I_4)来说,给定(I_1)和(I_4),这个模型预测(I_2),然后再把(I_1)和(I_4)调换一下,用同样的模型预测(I_3)
作者说他也试了每一层都这么插,最后(n=27),但是性能变差了
所以把(N)帧的视频分成(lceil N/n ceil)组图片,每组独立的插值
比特率优化:第(l)层用(K_l)个比特位来编码一张图像
目标是最小化总比特率,但保持所有编码帧的低失真
用基于beam search的启发式比特率选择方法。先列出I帧模型的所有不同的(m)种可能,先用(m)种可能的比特率试试第一个插值模型,得到(m^2)种组合。当然这些组合中不是所有的都能得到好的MS-SSIM per bitrate效果。把那些不在包络线(envelope)上的组合丢掉,发现只剩下(O(m))种组合,对每一层都这样,最后搜索空间为(O(Lm^2)),实际中会产生好的比特率