啊哈，算法自学记——9th

最短路径：

找出1号点到5号点的最短路径（单向路线）

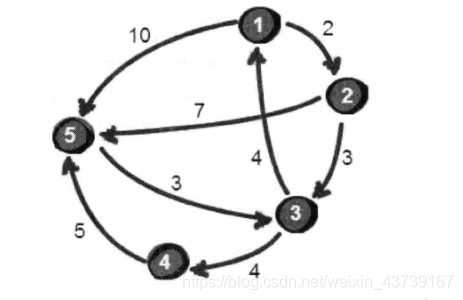
首先，5个点用个5*5的二维数组来存储这个地图

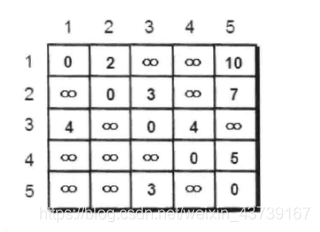
空格的值代表两个点之间的距离，∞表示无法到达，用999999来代替

#include <stdio.h>

int n,e[101][101],book[1001],min=999999;

void dfs(int cur,int dis)
{
    if (dis>min)
    {
        return;
    }

    if (cur==n)//如果到达目的地
    {
        if (dis<min)
        {
            min=dis;
        }
        return;
    }
    
    for (int i = 1; i <= n; i++)//从1~n一个一个试
    {
        if (e[cur][i]!=9999999 && book[i]==0)//如果可以走并且没走过
        {
            book[i]=1;//标记该点
            dfs(i,dis+e[cur][i]);//从这个点继续下一个
            book[i]=0;//之前的点探索完毕之后，取消该点标记
        }
        
    }
    
    
}

int main(int argc, char const *argv[])
{
    int i,j,m,a,b,c;
    printf("Input the size of the map:
");
    scanf("%d %d",&n,&m);
    //初始化二维数组
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=m;j++)
        {
            if (i==j)
            {
                e[i][j]=0;
            }
            else
            {
                e[i][j]=9999999;
            }    
        }
    }

    //读取点与点之间的道路以及距离
    for (int i = 1; i <= m; i++)
    {
        printf("Input the line and distance:
");
        scanf("%d %d %d",&a,&b,&c);
        e[a][b]=c;
    }
    
    book[1]=1;//从一号点出发
    dfs(1,0);

    printf("The min distance is :%d
",min);

    return 0;
}

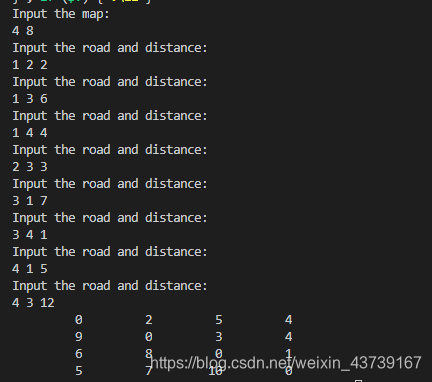
运行结果：

Floyd-Warshall

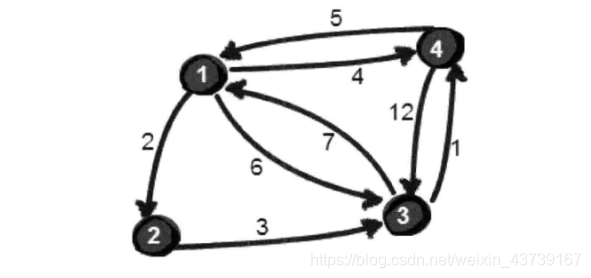
上图中有4个城市8条公路，公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短程，也就是求任意两个点之间的最短路径。这个问题也被称为“多源最短路径”问题。

#include <stdio.h>


int main(int argc, char const *argv[])
{
    int e[10][10],m,n,t1,t2,t3;
    
    //读入n与m,n代表顶点个数，m代表路径数量
    printf("Input the map:
");
    scanf("%d %d",&n,&m);

    for(int i = 1;i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            if(i==j)
                e[i][j]=0;
            else
                e[i][j]=9999999;
        }
    }

    //读入路径
    for (int i = 0; i < m; i++)
    {
        printf("Input the road and distance:
");
        scanf("%d %d %d",&t1,&t2,&t3);
        e[t1][t2]=t3;
    }
    

    //Floyd-Warshall核心算法
    for (int k = 1; k <= n; k++)
    {
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= n; j++)
            {
                if(e[i][j]>(e[i][k]+e[k][j]))
                {
                    e[i][j]=e[i][k]+e[k][j];
                }
            }
            
        }
        
    }
    //输出结果
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            printf("%10d",e[i][j]);
        }
        printf("
");
    }
    
    return 0;
}

运行结果：