啊哈，算法自学记——6th

深度优先搜索

全排列问题：
理解深度优先搜索的关键在于：
解决当下该如何做，至于下一步该如何做则与当下该如何做是一样的的操作。
深度优先搜索基本模型

void dfs(int step)
{
	判断边界
	尝试每一种可能for(int i=1;i<=n;i++)
	{
		继续下一步dfs(step+1);
	}
	return;
}

#include <stdio.h>

int a[10],book[10],n;//C语言的全局变量在没有赋值前默认为0，所以数组不用赋值了

void dfs(int step)//step表示站在第几个盒子面前
{
    int i;
    if(step==(n+1))//表示前面n 个盒子已经安排好了
    {
        //输出一种排列，（1-n盒子中的扑克牌编号）
        for (int  i = 1; i <= n; i++)
        {
            printf("-%d",a[i]);  
        }
        printf("
");
        return;//返回之前一步，也即最近调用dfs函数的地方
    }
    //此时站在第step个盒子面前，应该放那张牌呢？
    //按照 1-2-3-4-----n的顺序一一尝试
    for (int i = 1; i <= n; i++)
    {
        if(book[i]==0)//如果扑克i还在手上
        {
            //开始 常识使用扑克i
            a[step]=i;//将扑克i放入第step个盒子中
            book[i]=1;//表示扑克i已经不在手中

            //第step个盒子已经放好扑克牌，接下来需要走到下一个盒子面前
            dfs(step+1);//通过函数的递归调用来实现
            book[i]=0;//将刚才常识的扑克牌收回，才能进行下一次的常识
        }
    }
    return;
}


int main(int argc, char const *argv[])
{
    printf("Input a int num between 0-9:
");
    scanf("%d",&n);
    dfs(1);//首先站到第一个盒子面前
    return 0;
}

运行结果：

用深度优先搜索解决：口口口+口口口=口口口的问题
（填入1~9，每个只能用一次，使等式成立）

#include <stdio.h>

/*解决abc+efg=hij的问题
*数字为1~9
*/

int n,a[10],book[10];//全局变量默认值为0


void dfs(int step)
{
    int i;
    if(step==10)//n 个数，此时说明前面的n 个数已经安排好了
    {
        if (((a[1]*100+a[2]*10+a[3])+(a[4]*100+a[5]*10+a[6]))==(a[7]*100+a[8]*10+a[9]))
        {
            printf("%d%d%d+%d%d%d=%d%d%d
",a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9]);//打印已经安排好的排列
            n++;
        }
         return;
    }

    for(int i=1;i<=9;i++)
    {
        if (book[i]==0)//说明牌还在手上     
        {
            a[step]=i;
            book[i]=1;

            dfs(step+1);
            book[i]=0;
        }
        
    }
    return;
}

int main(int argc, char const *argv[])
{
    dfs(1);
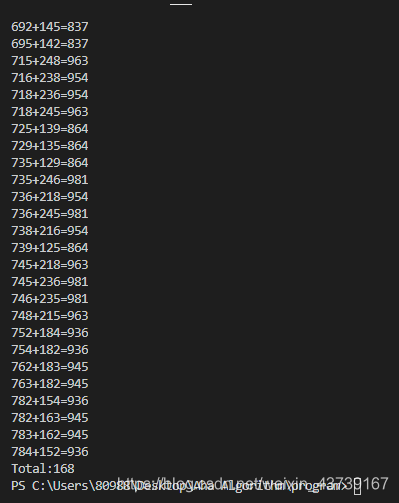
    printf("Total:%d
",n/2);
    return 0;
}

运行结果：

深度优先搜索，迷宫寻找小哈：

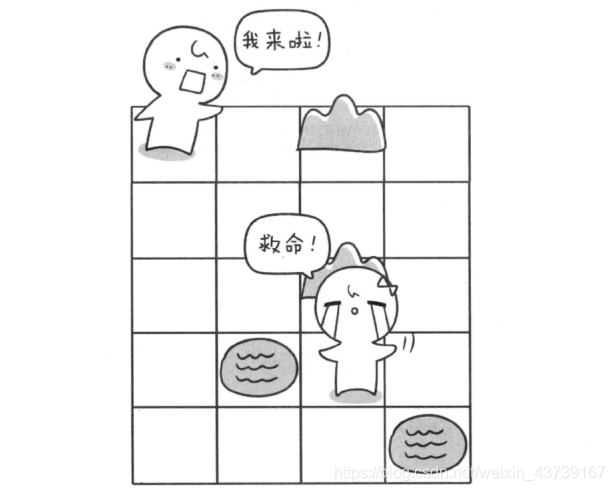
最开始在（1,1）只能向右走或者向下走，一个小哼只能向下走或者向右走，我们这里一个一个试，先让小哼向右走，走不通的时候在想下走，这里我们规定走的方向为： 右、下、左、上

用深度优先搜索来解决：
dfs()函数解决的功能是，当前应该怎么办，而当小哼在某个点的时候应该处理的是：先判断是否已经到达小哈的位置，如果没有到达则找到下一步的位置。

#include <stdio.h>

int m,n,q,p,min=999999;

int a[51][51],book[51][51];

void dfs(int x,int y,int step)
{
    int next[4][2]={//这里的x和y代表的是行和列，
        {0,1},//向右走**也即行不变，列+1
        {1,0},//向下走**列不变，行+1
        {0,-1},//向左走**行不变，列-1
        {-1,0}//向上走**行-1，列不变
    };

    int tx,ty,k;
    //判断是否到达小哈的位置
    if(x==p && y==q)
    {
        if(step<min)
            min=step;
        return;
    }

    //枚举四种走法，方向为右、下、左、上
    for (k = 0; k <= 3; k++)
    {
        //计算下一个点的坐标
        /*当k=0时，tx=x+0;ty=y+1;
         *当k=1时，tx=x+1;ty=y+0;
         *当k=2时，tx=x+0;ty=y-1;
         *当k=3时，tx=x-1;ty=y+0;
        */
        tx=x+next[k][0];
        ty=y+next[k][1];

        //判断是否越界
        if (tx<1||ty<1||tx>n||ty>m) 
        {
            continue;//下面的代码不执行，重新回归继续for循环
        }
        //判断该点是否为障碍物或者已经在路径之中
        if (a[tx][ty]==0 && book[tx][ty]==0)//如果该点，也就是计算出来的下一个点，既不是障碍物又不在已走过的路径中
        {
            book[tx][ty]=1;//标记该点已经走过
            dfs(tx,ty,step+1);//开始尝试下一个点，尝试每一种可能
            book[tx][ty]=0;//尝试结束， 取消这个点的标记
        } 
    }
    return;
}

int main(int argc, char const *argv[])
{
    int i,j,startx,starty;
    //读入迷宫的行和列，n为行，m为列
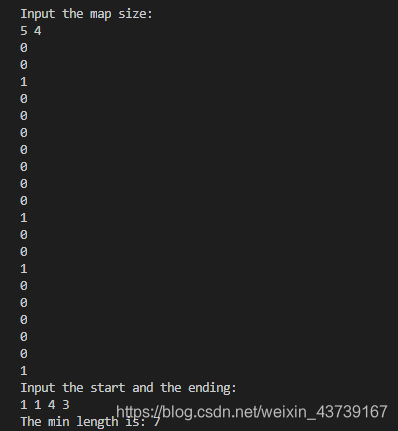
    printf("Input the map size:
");
    scanf("%d %d",&n,&m);
    //读取迷宫
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=m;j++)
        {
            scanf("%d",&a[i][j]);//二维数组a用来保存地图
        }
    }

    //读入迷宫的起点和终点
    printf("Input the start and the ending:
");
    scanf("%d %d %d %d",&startx,&starty,&p,&q);
    //从起点开始搜索 
    book[startx][starty]=1;//标记起点已经在路径中，防止重复走----二维数组book用来存储已经走过的点

    dfs(startx,starty,0);//从起点开始，走过的路程为0
    printf("The min length is: %d
",min);
    return 0;
}

运行结果：