647. 回文子串
题目描述
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:"abc" 输出:3 解释:三个回文子串: "a", "b", "c"
示例 2:
输入:"aaa" 输出:6 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
提示:
输入的字符串长度不会超过 1000 。
思路一:暴力循环
暴力三循环,一共有 n(n+1)/2个子串,分别判断每个子串是否是回文串
1 class Solution { 2 public int countSubstrings(String s) { 3 // 暴力三循环,一共有 n(n+1)/2个子串,分别判断每个子串是否是回文串 4 if(s == null || s.length() == 0){ 5 return 0; 6 } 7 int count = 0; 8 for(int i = 0; i < s.length(); i++){ 9 for(int j = i; j < s.length(); j++){ 10 boolean flag = true; 11 for(int k = 0; k < (j - i + 1)/2; k++){ 12 if(s.charAt(k+i) != s.charAt(j-k)){ 13 flag = false; 14 break; 15 } 16 } 17 if(flag == true){ 18 count++; 19 } 20 } 21 } 22 return count; 23 } 24 }
leetcode 执行用时:620 ms > 6.67%, 内存消耗:37 MB > 59.58%
复杂度分析:
时间复杂度:很明显三个for循环,所以时间复杂度为O(n3)
空间复杂度:O(1)
思路二:动态规划
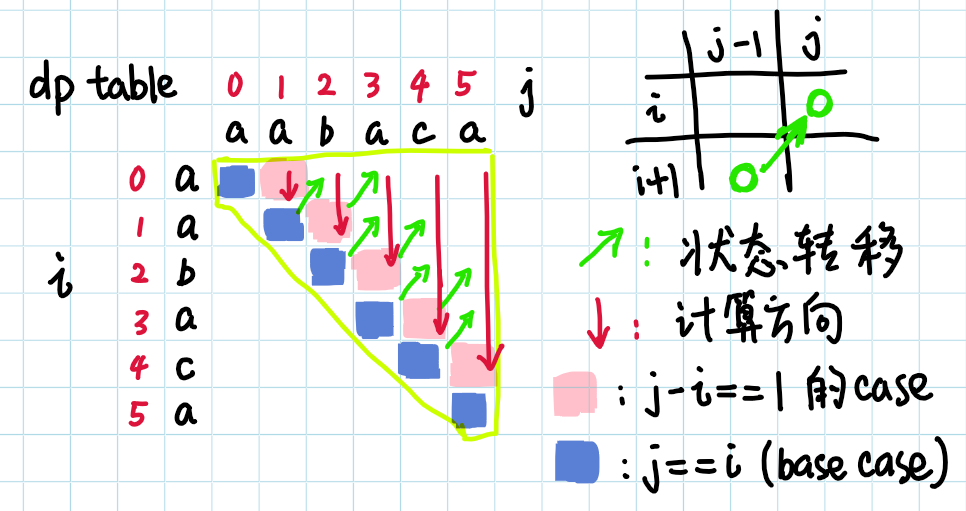
1 class Solution { 2 public int countSubstrings(String s) { 3 4 if(s == null){ 5 return 0; 6 } 7 int count = 0; 8 int len = s.length(); 9 boolean[][] dp = new boolean[len][len]; 10 // 因为转态转移方程中求dp[i][j]时用到了dp[i+1][j], 所以我们的外层循环应该循环j 11 for(int j = 0; j < len; j++){ 12 for(int i = 0; i <= j; i++){ 13 // 如果区间两端字符相等,且区间长度小于等于2或者大于2但是内部是回文串,那么整个区间都是回文串 14 if(s.charAt(i) == s.charAt(j) && ((j-i) < 2 || dp[i+1][j-1])){ 15 count++; 16 dp[i][j] = true; 17 } 18 } 19 } 20 return count; 21 } 22 }
复杂度分析:
空间优化
其实这个空间复杂度还可以再降低一些,那就是借助一维矩阵而非二维矩阵,因为dp[i][j]只与 dp[i+1][j-1]有关,也就是只与前一列有关,所以我们用一个一维矩阵,只存储原来二维矩阵中一列的值,dp[i] 就只与dp[i+1]有关,因为上一个dp[i+1]肯定是比当前列小一的,所以默认就是dp[i+1][j-1], 很巧妙。我见过还有一题也用到了这样的一个技巧,就是求一个从矩阵左上角到右下角路径最大和。
1 class Solution { 2 public int countSubstrings(String s) { 3 4 if(s == null){ 5 return 0; 6 } 7 int count = 0; 8 int len = s.length(); 9 boolean[] dp = new boolean[len]; 10 // 因为转态转移方程中求dp[i][j]时用到了dp[i+1][j], 所以我们不按行遍历,而是按列遍历 11 for(int j = 0; j < len; j++){ 12 for(int i = 0; i <= j; i++){ 13 // 如果区间两端字符相等,且区间长度小于等于2或者大于2但是内部是回文串,那么整个区间都是回文串 14 if(s.charAt(i) == s.charAt(j) && ((j-i) < 2 || dp[i+1])){ 15 count++; 16 dp[i] = true; 17 }else{ 18 // 因为这个dp[i]其实是原来的dp[i][j],所以这里必须置为false, 19 // 如果没有置为false, 可能会沿用上一轮的值,导致真实值不正确 20 dp[i] = false; 21 } 22 } 23 } 24 return count; 25 } 26 }
leetcode 执行时间为:11 ms > 42.49%, 内存消耗:36.6 MB > 97.37%, 可以看到这个内存效率高了不少
复杂度分析:
思路三:中心扩展法
选定中心点后,同时判断左右字符是否相等,如果相等,则构成了回文子串,再继续向左右扩张,判断是否能形成更长的回文子串。
首先每个字符都可以是中心点,其次所有相邻的两个字符也可以中心点,比如abba, 如果以单个字符中心点,那么abba这最长的回文子串就永远统计不到,但是如果以 bb 为中心点,则能统计到这个回文子串。
至于为什么三个相邻的字符,四个相邻的字符不是中心点,因为三个相邻的字符可以是单个中心点扩展一次得到,四个相邻的字符可以是两个相邻的字符扩展一次得到。所以中心点的个数为 2n-1, n 字符串长度。
1 class Solution { 2 public int countSubstrings(String s) { 3 4 if(s == null){ 5 return 0; 6 } 7 int count = 0; 8 int len = s.length(); 9 for(int center = 0; center < 2 * len -1; center++){ 10 int left = center / 2; // 如果center是奇数,则left和right则是两个相邻的字符 11 int right = center / 2 + center % 2; // 如果center是偶数,则left和right是同个字符 12 while(left >= 0 && right < len && s.charAt(left) == s.charAt(right)){ 13 count++; 14 left--; 15 right++; // 向左右扩张一次 16 } 17 } 18 return count; 19 } 20 }
leetcode 执行用时:6 ms > 51.97%, 内存消耗:37.1 MB > 55.85%, 可以看到这个执行时间是动态规划的一半
复杂度分析:
时间复杂度:只有一个for循环,所以时间复杂度为O(n)
空间复杂度:O(1)