三角形相关算法--求解线段端点坐标

问题描述：

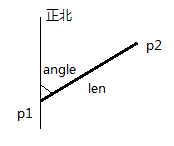
　　已知线段一个顶点p1的坐标(x1,y1)，p1与p2的距离len，p1-p2与正北方向的夹角angle，计算p2的坐标(x2,y2)。

求解思路：

　　1、根据p1、p2的距离可以列出一个等式：

(p2.x-p1.x)²+(p2.y-p1.y)²=len²

　　2、根据p1-p2与正北方向的夹角可以列出一个等式：

tan(angle)=(p2.x-p1.x)/(p2.y-p1.y)

　　根据这两个等式，可推导出p2.x、p2.y的值。

　　3、在推导过程中，p2.y-p1.y被用作分母，因此，在实际计算中，需要单独考虑angle=90度和270度的情况（即p1-p2水平的情况）。

C#算法：

/// <summary>
/// 已知线段的一个端点坐标、线段长度、线段与正北的夹角（0-359度），夹角的顶点为已知点
/// 求解另一个端点的坐标
/// </summary>
/// <param name="p1">已知端点坐标</param>
/// <param name="len">线段长度</param>
/// <param name="angle">与正北的夹角（单位：弧度）</param>
/// <returns>另一个端点坐标</returns>
public static TwoDimPoint GetVertex(TwoDimPoint p1, double len, double angle)
{
    TwoDimPoint result = new TwoDimPoint();

    angle %= 2 * Math.PI;//限制角度在0到359之间

    if (angle == Math.PI / 2 || angle == Math.PI * 3 / 2)//角度为90或270度
    {
        result.Y = p1.Y;
        if (angle < Math.PI)
            result.X = p1.X + len;
        else
            result.X = p1.X - len;
    }
    else
    {
        double A = len / Math.Sqrt(Math.Tan(angle) * Math.Tan(angle) + 1);
        if (angle > Math.PI / 2 && angle < Math.PI * 3 / 2)
            result.Y = p1.Y - A;
        else
            result.Y = p1.Y + A;
        result.X = (result.Y - p1.Y) * Math.Tan(angle) + p1.X;
    }

    return result;
}

其他相关算法：

三角形相关算法--求解三角形顶点坐标