无约束问题
无约束问题定义如下：
f(x)称为目标函数, 其中x是一个向量，它的维度是任意的。
通过求导， 令导数等于零即可：
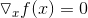
如下图所示：
等式约束问题
单约束问题
单约束问题定义如下：
g(x)称为约束函数
单约束问题的解决步骤如下：
1， 加一个变量，这个变量称为拉格朗日乘子将约束条件和目标函数联立构造拉格朗日函数
2， 对每个变量分别求导， 令导数等于零，求得最优值
这是一个例子：
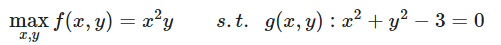
使用一个约束，一个拉格朗日乘子，得到拉格朗日函数：
求导得到：
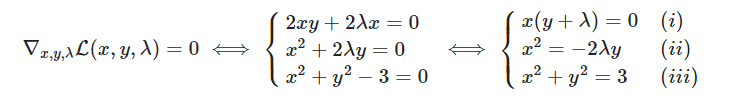
解得：
代入f（x， y）可得2， -2， 0， 也就是我们的最优值
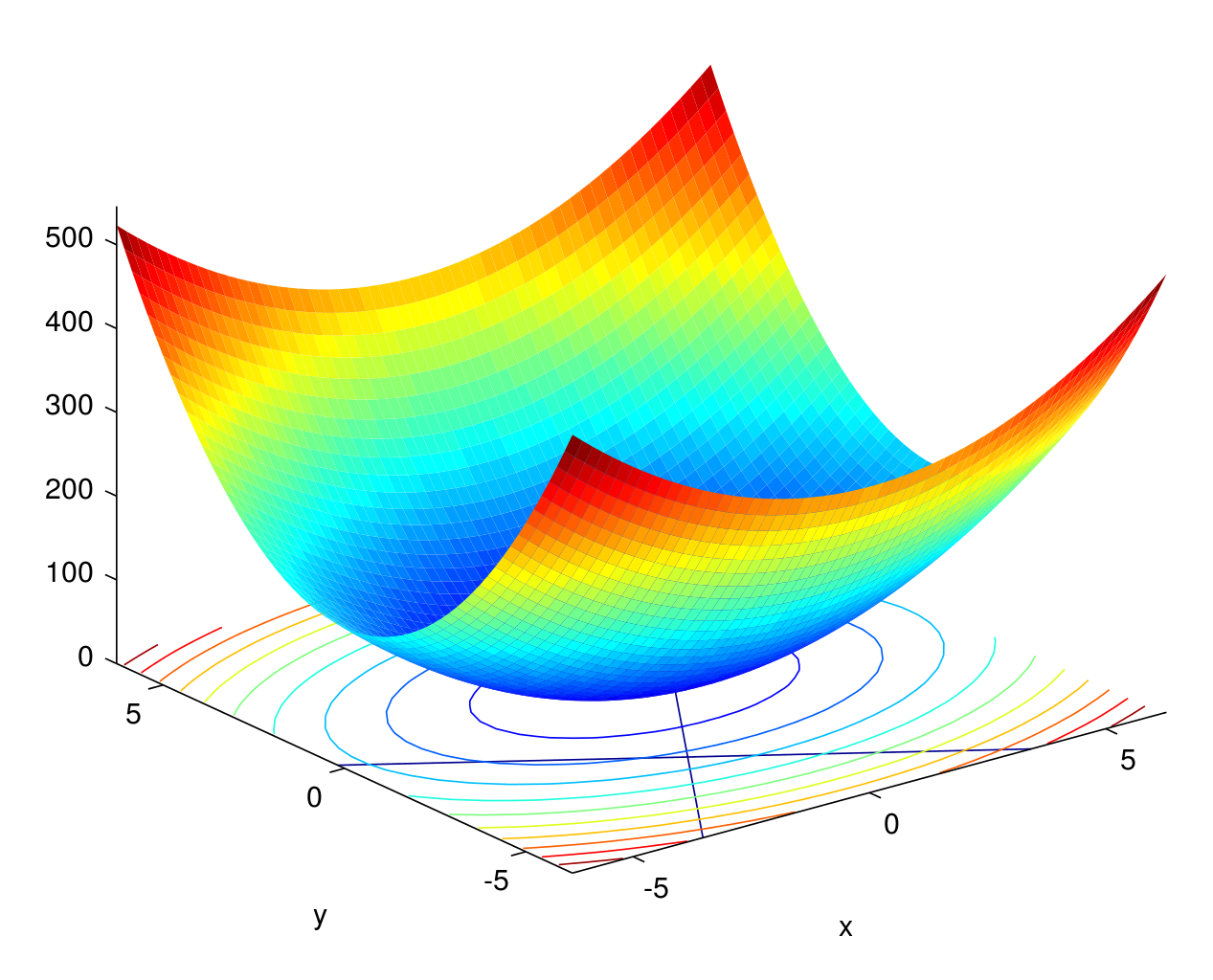
约束函数的即是一维空间的圆圈，变成目标函数的约束条件嵌入到目标函数的曲面中,整个过程如图:
多约束问题
等式约束的多约束问题即有多个约束函数， 多约束问题的定义如下：
多约束的问题和单约束问题的解决过程类似：
1， 加k个拉格朗日乘子，将约束条件和目标函数联立构造拉格朗日函数
2， 对每个变量分别求导， 令导数等于零，求得最优值
在约束线上找到一个点可以和等高线相切，所得的值实在约束范围内的最大值或者最小值如下面两个图， 分别是原图和等高线图
不等式约束问题
不等式问题单约束问题定义如下：
多约束的问题定义如下：
单约束和多约束问题的解法是类似的，下面以分析单约束问题为例。
不等式的约束，会出现两种情况，一种是最优解不在不等式的约束中，我们称为约束无效（下图左）， 一种是在不等式的约束中，约束有效（下图右）。
情况一：约束无效
如图左，由于最优点在可行域内， 约束了跟没约束一样，由于等价于没有约束作用，所以直接可以对 f(x)+λh(x) 用拉格朗日乘子法
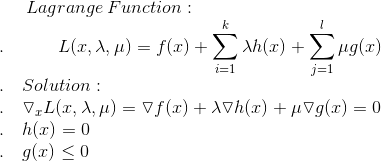
情况二：约束有效
如图右，由于有约束的作用，约束条件最弱的时候取得最优值，可以看出， 最优解在可行域的边界上取得，转化成了等式约束，因此，不等式约束变成了等式约束。
（我也不想用可以看出的， 但是确实是这样，从等高图直观的来看， 可行域里面的等高更高，边界才有可能取得最优解）
h(x), g(x) 为0没有问题，但是为什么
大于 0 呢？后面通过例题来解释（先记住，俺也没咋搞懂， 老师跟我说这里很简单，但是他也记不得了，我搜了一堆博客，大部分都是用梯度解释的【惨兮兮）。
综上， 在情况一下，μ=0 且 g(x)≤0，情况二下，μ≥0 且 g(x)=0，将上面的条件综合起来， 写成多约束的形式，即可以得到大名鼎鼎的KKT条件：
一个例子
对于情况一，问题如下：
这个不等式约束包含了原点， 求它相当于没有求， 属于约束无效， 如图：
对于情况二，问题如下：
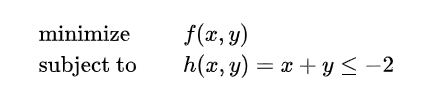
这个不等式不包含原点， 在不等式约束下，最小值是在边缘相切的地方取得，和用等式h(x,y)=x+y=-2进行约束效果是一样的，如图：
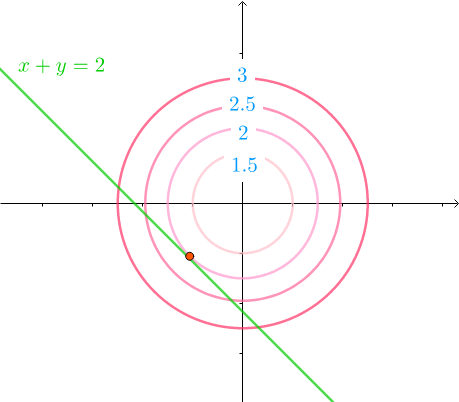
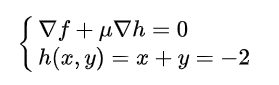
但是这里又不能完全等价为等式约束， 因为不等式带来了新的条件， 就是我们需要解释的μ
如图， 同心圆是凸函数的等高线，等高线的值如下排列，所以在相切处，法线也就是
的方向如下（法线也就是梯度，指向增长或下降最快的方向，这里用的是增长的， 也就是等高线的值变大的方向）
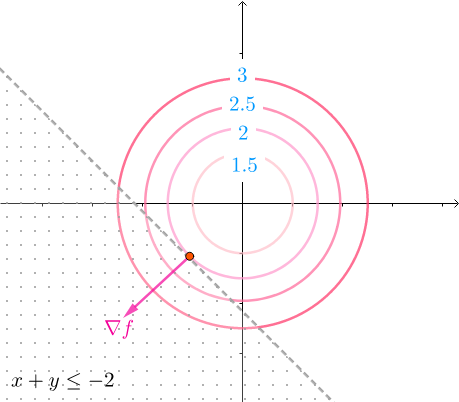
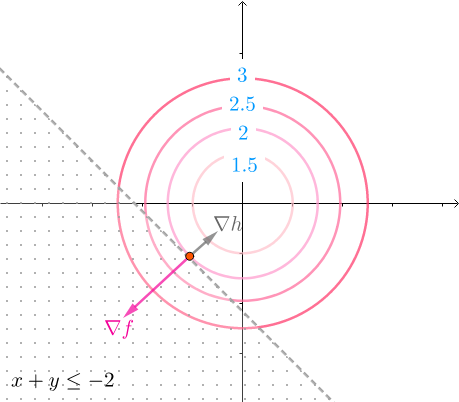
而凸函数h(x,y)的法线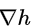
也一样指向h(x,y)增长的方向，这个方向正好和相反：
因此， 我们有
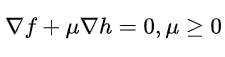
μ ≥ 0说明了两个梯度是方向是相反的。
KKT总结：
各个项以及对应的含义如下：
