线性可分支持向量机与软间隔最大化--SVM
### 给定线性可分的数据集
假设输入空间(特征向量)为,输出空间为。
输入
表示实例的特征向量,对应于输入空间的点;
输出
表示示例的类别。
我们说可以通过**间隔最大化**或者等价的求出相应的**凸二次规划问题**得到的**分离超平面**

以及决策函数:
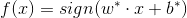
但是,上述的解决方法对于下面的数据却不是很友好, 例如,下图中黄色的点不满足间隔大于等于1的条件
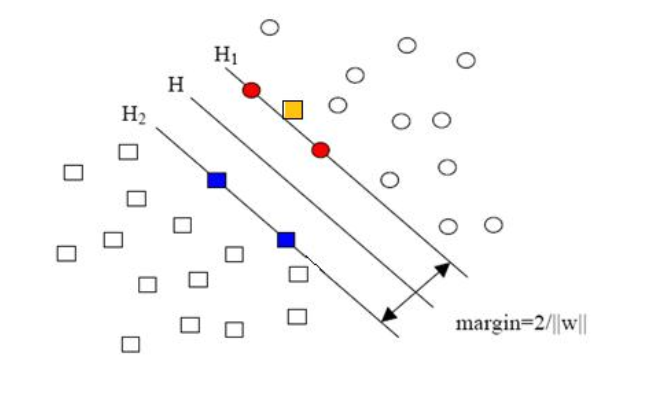
这样的数据集不是线性可分的, 但是去除少量的异常点之后,剩下的点都是线性可分的, 因此, 我们称这样的数据集是近似线性可分的。
对于近似线性可分的数据集,我们引入了松弛变量 ,使得函数间隔加上松弛变量大于等于1。这样就得到了下面的解决方案:
,使得函数间隔加上松弛变量大于等于1。这样就得到了下面的解决方案:
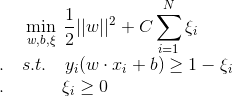
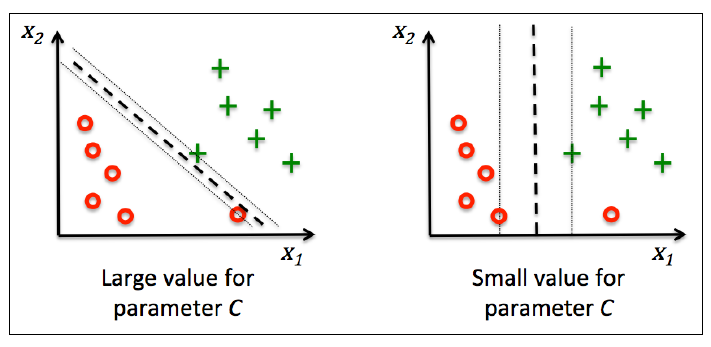
其中,每个样本点都对应一个松弛变量, C > 0 称为**惩罚参数**。C越大,对误分类的点的惩罚越大。
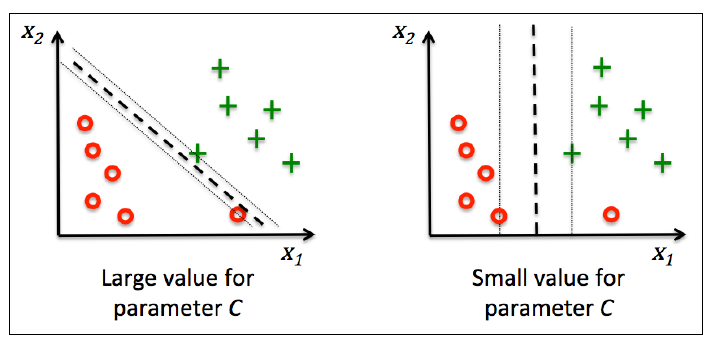
这个解决方案旨在使得**间隔最大化的同时减少误分类个数**。下图是C对分类的影响,左图是大C, 右图是小C:
可以证明w是唯一的, 但是b不唯一,而是存在一个区间
### 下面来解决这个问题
首先引入拉格朗日函数(Lagrange Function):
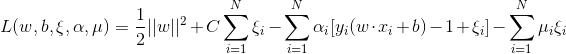
他的对偶问题(参考拉格朗日对偶性(Lagrange duality))是极大极小问题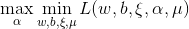 , 首先求
, 首先求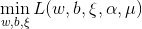 。对
。对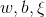 求导,解法如下:
求导,解法如下:
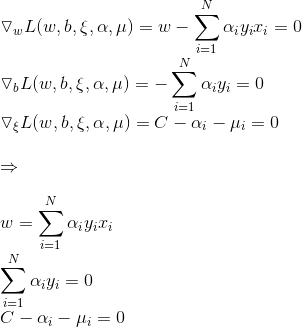
代入得到:
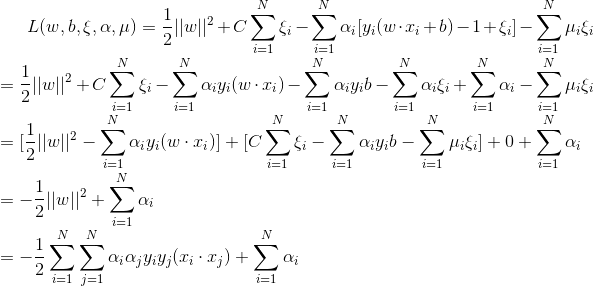
问题转化为:
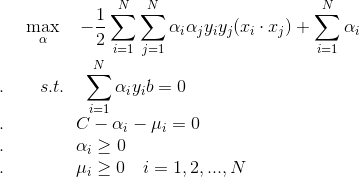
怎么求最优的w*, b*呢?
我们来看,原问题的KKT条件如下:

根据KKT条件的性质可以知道(参考[拉格朗日乘子(Lagrange multify)和KKT条件](https://www.cnblogs.com/hichens/p/11863780.html)):
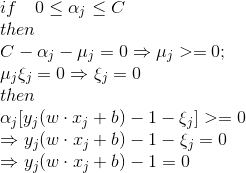
所以可以求得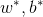:
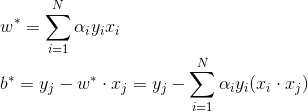
## 综上, 引入松弛变量后线性支持向量机算法为:
.
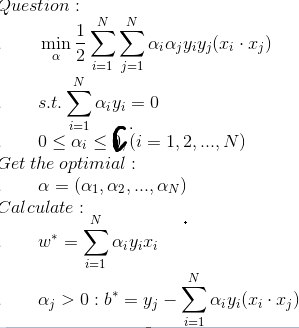
*我们引入的松弛变量去哪里了呢?为什么算法中没有了?
其实, 松弛变量 在通过惩罚参数C隐式的作用。
在通过惩罚参数C隐式的作用。
我们可以改变C值,看看改变C哪些变量会随着改变。
增大C,由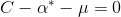 知,
知,  就更有可能大于0, 再根据
就更有可能大于0, 再根据 ,松弛变量
,松弛变量 取0就更简单, 这样就没有约束作用了。对整个数据集来说相当于是小的约束作用。
取0就更简单, 这样就没有约束作用了。对整个数据集来说相当于是小的约束作用。
反之也可推出约束作用更强。
可以用这张图来解释:
 ,使得函数间隔加上松弛变量大于等于1。这样就得到了下面的解决方案:
,使得函数间隔加上松弛变量大于等于1。这样就得到了下面的解决方案: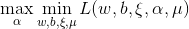 , 首先求
, 首先求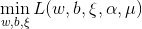 。对
。对 求导,解法如下:
求导,解法如下: 在通过惩罚参数C隐式的作用。
在通过惩罚参数C隐式的作用。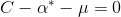 知,
知,  就更有可能大于0, 再根据
就更有可能大于0, 再根据 ,松弛变量
,松弛变量 取0就更简单, 这样就没有约束作用了。对整个数据集来说相当于是小的约束作用。
取0就更简单, 这样就没有约束作用了。对整个数据集来说相当于是小的约束作用。