线性回归

1.表达形式：

一个示例有 d$d$d个属性：x⃗ =(x1,x2,...,xd)$vec{x}=(x_1, x_2,...,x_d)$x=(x1​,x2​,...,xd​)，其表达形式为：
f(x)=wTx+b(1.1)$f(x)=w^Tx+b ag{1.1}$f(x)=wTx+b(1.1)
其中w=(w1,w2,...,wd)$w=(w_1, w_2, ..., w_d)$w=(w1​,w2​,...,wd​)

---

2.标准线性回归

令预测值与真实值的均方根误差最小化
(w∗,b∗)=argmin(w,b)∑i=1m(f(xi)−yi)2(2.1)$egin{aligned}(w^*,b^*)=mathop{argmin}_{(w,b)} sum_{i=1}^{m}(f(x_i)-y_i)^2 ag{2.1}end{aligned}$(w∗,b∗)=argmin(w,b)​i=1∑m​(f(xi​)−yi​)2​(2.1)

2.1 线性回归（二元一次函数，此时w$w$w是一个数）

2.1.1均方误差最小化

(w∗,b∗)=argmin(w,b)∑i=1m(w⋅xi+b−yi)2(2.2)$egin{aligned}(w^*,b^*) =mathop{argmin}_{(w,b)} sum_{i=1}^{m}(w·x_i + b-y_i)^2 ag{2.2}end{aligned}$(w∗,b∗)=argmin(w,b)​i=1∑m​(w⋅xi​+b−yi​)2​(2.2)

2.1.2最小二乘参数估计

令：E(w,b)=∑mi=1(w⋅xi+b−yi)2$E_{(w,b)}=sum_{i=1}^{m}(w·x_i+b-y_i)^2$E(w,b)​=∑i=1m​(w⋅xi​+b−yi​)2，对w,b$w,b$w,b求导，令导数为0，解得w,b$w,b$w,b分别为：
w=∑mi=1yi(xi−x¯)∑mi=1x2i−1m(∑mi=1xi)2(2.3)$w=frac {sum_{i=1}^{m}y_i(x_i-ar{x})}{sum _{i=1}^{m} {x^2_i}- frac {1}{m}(sum_{i=1}^{m}x_i)^2} ag{2.3}$w=∑i=1m​xi2​−m1​(∑i=1m​xi​)2∑i=1m​yi​(xi​−xˉ)​(2.3)

b=1m∑mi=1(yi−wxi)(2.4)$b=frac {1}{m}sum_{i=1}^{m}(y_i-wx_i) ag{2.4}$b=m1​i=1∑m​(yi​−wxi​)(2.4)

2.2 多元线性回归（此时w$w$w是一个向量）

令设训练样本共有m$m$m个，每个样本有d$d$d个属性，把b$oldsymbol{b}$b与x$oldsymbol{x}$x写到一起，记为X$oldsymbol{X}$X，则X$oldsymbol{X}$X为：

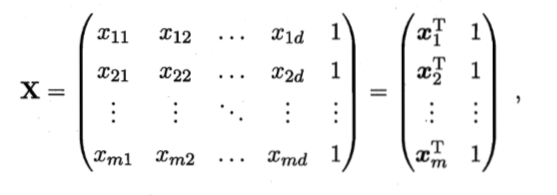
根据向量求模长的公式，可写为
E(w∗,b)=argmin(w∗)(y−X⋅wT)T⋅(y−X⋅wT)(2.5)$egin{aligned}E_{(oldsymbol{w^*, b})}= mathop{argmin}_{(oldsymbol{w^*})} (oldsymbol{y}-oldsymbol{X}·oldsymbol{w^T})^T ·( oldsymbol{y}-oldsymbol{X}·oldsymbol{w^T} ) ag{2.5}end{aligned}$E(w∗,b)​=argmin(w∗)​(y−X⋅wT)T⋅(y−X⋅wT)​(2.5)

令Ewˆ=(y−X⋅wT)T⋅(y−X⋅wT)$E_{oldsymbol{hat{w}}}=(oldsymbol{y}-oldsymbol{X}·oldsymbol{w^T})^T ·(oldsymbol{y}-oldsymbol{X}·oldsymbol{w^T})$Ew^​=(y−X⋅wT)T⋅(y−X⋅wT)

考虑矩阵求导：

所以，对Ewˆ$E_{oldsymbol{hat{w}}}$Ew^​求导，有

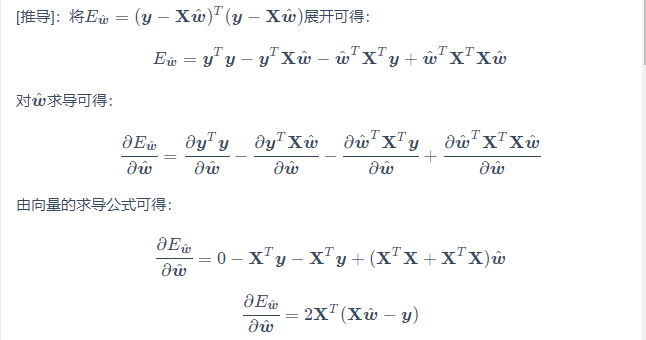
令∂Ewˆ∂wˆ=0$frac {partial{E_{oldsymbol{hat{w}}}}}{partial{hat{w}}}=0$∂w^∂Ew^​​=0，考虑下列两种情况：

• 当X$oldsymbol{X}$X为满秩矩阵时：
  wˆ∗=(XTX)−1XTy$oldsymbol{hat{w}^*}=oldsymbol{(X^TX)^{-1}X^Ty}$w^∗=(XTX)−1XTy，令xˆ=[x,1]$oldsymbol{hat{x}}=[oldsymbol{x}, 1]$x^=[x,1]，则学习到的模型为：
  f(xˆi)=xˆi(XTX)−1XTy(2.6)$egin{aligned}f(oldsymbol{hat{x}_i})=oldsymbol{hat{x}_i}oldsymbol{(X^TX)^{-1}}oldsymbol{X^Ty} ag{2.6}end{aligned}$f(x^i​)=x^i​(XTX)−1XTy​(2.6)
• 当X$oldsymbol{X}$X为非满秩矩阵时（数据条数少于未知数个数）：
  在这样的情况下，可能有多个解（wˆ$oldsymbol{hat{w}}$w^）此时需要考虑正则化

---

3 局部加权线性回归

由于线性回归求的是具有最小均方误差的无偏估计，因此通常伴随着欠拟合的现象，一些方法会在估计方法中加入偏差，降低预测的均方误差。

3.1 基本思想

通过给待预测点附近的每个点赋予一定的权重，然后在这个子集上进行普通的回归（设计代价函数时，待预测点附近的点拥有更高的权重，权重随着距离的增大而缩减——这也就是名字中“局部”和“加权”的由来。）
那么，原本均方误差最小化的表达式为（公式2.2）：
(w∗,b∗)=argmin(w,b)∑i=1m(∑j=1pwj⋅xij+b−yi)2(2.2)$egin{aligned}(w^*,b^*) =mathop{argmin}_{(w,b)} sum_{i=1}^{m}(sum_{j=1}^{p}w_j·x_{ij} + b-y_i)^2 ag{2.2}end{aligned}$(w∗,b∗)=argmin(w,b)​i=1∑m​(j=1∑p​wj​⋅xij​+b−yi​)2​(2.2)
现在，我们把每一个点都赋予一定的权重（用θi$heta_i$θi​表示第i$i$i个点的权重），目标是：离真实值越近，赋予的权重越大。因此，修改公式为：
(w∗,b∗)=argmin(w,b)∑i=1mθi⋅(∑j=1pwj⋅xij+b−yi)2(3.1)$egin{aligned}(w^*,b^*) =mathop{argmin}_{(w,b)} sum_{i=1}^{m} heta_i·(sum_{j=1}^{p}w_j·x_{ij} + b-y_i)^2 ag{3.1}end{aligned}$(w∗,b∗)=argmin(w,b)​i=1∑m​θi​⋅(j=1∑p​wj​⋅xij​+b−yi​)2​(3.1)
公式(3.1)对权重w$w$w求导并令其为0：
∂(w∗,b∗)∂w∗→XTWy→W=−2XTθ(y−XW)=0=XTθXW=(XTθX)−1XTθy(3.2)$egin{aligned}frac {partial (w^*,b^*)}{partial w^*} &= -2 oldsymbol{X^T heta (y-XW) }=0 \ ightarrow oldsymbol{X^TWy} &= oldsymbol{X^T heta XW} \ ightarrow oldsymbol{W} &= oldsymbol{(X^T heta X)^{-1} X^T heta y} ag{3.2}end{aligned}$∂w∗∂(w∗,b∗)​→XTWy→W​=−2XTθ(y−XW)=0=XTθXW=(XTθX)−1XTθy​(3.2)

3.2 权重怎么取？

首先明确一点：局部加权线性回归是一个 非参数（non-parametric） 算法。之前学习的（不带权）线性回归算法是有 参数（parametric） 算法，因为它有固定的有限数量的，能够很好拟合数据的参数（权重）。一旦我们拟合出权重并存储了下来，也就不需要再保留训练数据样本来进行更进一步的预测了。相比而言，用局部加权线性回归做预测，我们需要保留整个的训练数据，每次预测得到不同的权重，即参数不是固定的。

术语 “非参数” 粗略意味着：我们需要保留用来代表假设 h的内容，随着训练集的规模变化是呈线性增长的。

3.3 机器学习-核函数（核模型）

局部加权线性回归使用“核”函数对附近的点赋予更高的权重，目前常用的类型就是高斯核，具体表达式为：
w(i,i)=exp(∣x(i)−x∣2−2k2)(3.3)$egin{aligned}w(i,i) &= exp(frac{|x^{(i)}-x|^2 } {-2k^2} ) ag{3.3}end{aligned}$w(i,i)​=exp(−2k2∣x(i)−x∣2​)​(3.3)

使用高斯核函数具有以下特征：

• 构建了一个只含有对角元素的权重矩阵w$w$w，当点x$x$x与x(i)$x^{(i)}$x(i)越接近，则w(i,i)$w(i,i)$w(i,i)将会越大，随着样本点与待预测点距离的递增，权重将会以指数级衰减。

• k$k$k能够控制衰减的速度。若k$k$k越大，则权重的宽度越大，衰减的速度越慢，容易导致欠拟合；若k$k$k越小，则权重的宽度越窄，衰减的速度越快，容易造成过拟合；<当k=1$k=1$k=1时，可认为是最小二乘法拟合的结果>

通常情况下，通过交叉验证或者网格搜索等方法确定最佳的k值。

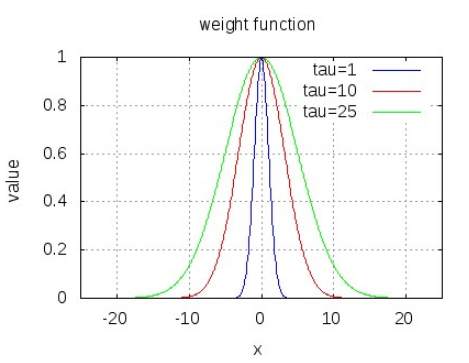
为什么高斯核是对角矩阵？
因为在矩阵中，只有对角线上的元素值表示的是x21,x22,...,x2n$x_1^2,x_2^2,...,x_n^2$x12​,x22​,...,xn2​的系数。

---

4 岭回归

上述两个方法：标准线性回归和局部加权线性回归都有一个重要基础——特征要比样本少，即输入数据的矩阵必须要是满秩矩阵。那么，当矩阵为非满秩矩阵时，都哪些处理方法？

在标准线性回归中，权重的值为：
wˆ∗=(XTX)−1XTy$oldsymbol {hat{w}^*} = oldsymbol{(X^TX)^{-1}X^Ty}$w^∗=(XTX)−1XTy

而岭回归的方法是在矩阵XTX$X^TX$XTX上加一个λI$lambda I$λI，即从对XTX$X^TX$XTX的逆转化为对XTX+λI$X^TX+lambda I$XTX+λI求逆，公式可写为：

wˆ∗=(XTX+λI)−1XTy(4.1)$egin{aligned}oldsymbol{hat{w}^*}=oldsymbol{(X^TX+lambda I)^{-1}X^Ty} ag{4.1}end{aligned}$w^∗=(XTX+λI)−1XTy​(4.1)
对比公式(2.2)可知，岭回归其实是优化下面这个问题：
(w∗,b∗)=argmin(w,b)∑i=1m(∑j=1pwj⋅xij+b−yi)2+λ∑j=1pw2j(4.2)$egin{aligned}(w^*,b^*) =mathop{argmin}_{(w,b)} sum_{i=1}^{m}(sum_{j=1}^{p}w_j·x_{ij} + b-y_i)^2 + lambda sum_{j=1}^{p}w_j^2 ag{4.2}end{aligned}$(w∗,b∗)=argmin(w,b)​i=1∑m​(j=1∑p​wj​⋅xij​+b−yi​)2+λj=1∑p​wj2​​(4.2)

岭回归的意义:
加上了L2范数（目标函数的惩罚函数），作用是确保权重值不会很大，起到收缩的作用。对于岭回归来说，随着λ$lambda$λ的增大，模型的方差会减少（XTX+λI$X^TX+lambda I$XTX+λI增大，(XTX+λI)−1$X^TX+lambda I)^{-1}$XTX+λI)−1减小，w$w$w减小，因此偏差增大，因此λ$lambda$λ能够平衡偏差与方差的关系。），·

4.1 岭回归的几何意义

{(w∗,b∗)=argmin(w,b)∑mi=1(∑pj=1wj⋅xij+b−yi)2附加约束条件：λ∑pj=1w2j≤t(4.3)$egin{aligned}left { egin{matrix}(w^*,b^*) =mathop{argmin}_{(w,b)} sum_{i=1}^{m}(sum_{j=1}^{p}w_j·x_{ij} + b-y_i)^2 \ 附加约束条件： lambda sum_{j=1}^{p}w_j^2 leq t& end{matrix} ight. ag{4.3}end{aligned}${(w∗,b∗)=argmin(w,b)​∑i=1m​(∑j=1p​wj​⋅xij​+b−yi​)2附加约束条件：λ∑j=1p​wj2​≤t​​​(4.3)

4.1.1 岭回归添加回归系数平方和的原因

为了解决多重共线性的麻烦。作者在《岭回归和LASSO回归的区别》中提到了一个很通俗的例子，一个家庭的收入和支出具有很强的共线性，但是在岭回归系数平方和的约束下，通过调整权重值，即使收入有很大的正数，支出为很小的负数，最后预测的结果也不会有较大的偏差，这就是岭回归系数平方和约束的作用。

4.1.2 岭回归系数的性质

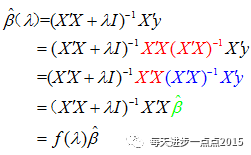
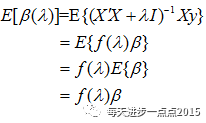
0时，岭回归系数具有压缩性">

4.1.3 岭参数的选择

我们知道岭回归系数会随着λ$lambda$λ的变化而变化，为保证选择出最佳的岭回归系数，该如何确定这个λ$lambda$λ值呢？一般我们会选择定性的可视化方法和定量的统计方法。对这种方法作如下说明：
1）绘制不同λ$lambda$λ值与对应的β$eta$β值之间的折线图，寻找那个使岭回归系数趋于稳定的λ$lambda$λ值；同时与OLS相比，得到的回归系数更符合实际意义；
2）方差膨胀因子法，通过选择最佳的λ$lambda$λ值，使得所有方差膨胀因子不超过10；
3）虽然λ$lambda$λ的增大，会导致残差平方和的增加，需要选择一个λ$lambda$λ值，使得残差平方和趋于稳定（即增加幅度细微）。

---

5 lasso 回归

上文提到，岭回归增加的约束是∑pk=1β2k≤t$sum_{k=1}^{p}eta_k^2 leq t$∑k=1p​βk2​≤t，那么在lasso回归中，添加的约束条件为：∑pk=1∣βk∣≤t$sum_{k=1}^{p}|eta_k| leq t$∑k=1p​∣βk​∣≤t

(w∗,b∗)=argmin(w,b)∑i=1m(∑j=1pwj⋅xij+b−yi)2+λ∑j=1p∣wj∣(5.1)$egin{aligned}(w^*,b^*) =mathop{argmin}_{(w,b)} sum_{i=1}^{m}(sum_{j=1}^{p}w_j·x_{ij} + b-y_i)^2 + lambda sum_{j=1}^{p} |w_j| ag{5.1}end{aligned}$(w∗,b∗)=argmin(w,b)​i=1∑m​(j=1∑p​wj​⋅xij​+b−yi​)2+λj=1∑p​∣wj​∣​(5.1)

若采用这种约束，当λ$lambda$λ足够小的时候，一些系数会因此衰减为0。

但是，在新的约束条件下，若要解出回归系数，则需要使用二次规划法算法

6 前向逐步回归

前向逐步回归算法利用了贪心算法的思想，具体算法伪代码如下：

---

代码实现

github翻我牌子