图同构的矩阵初等变换判定及算法设计

图同构问题

图同构就是从顶点和边的拓扑图结构上来看, 两个图是否有可能以同样的方式画出。从邻接矩阵角度来看, 通过对其中一个邻接矩阵施加一系列的行和列的矩阵初等变换, 能否使两者相等( 即同构)或永远无法相等( 即不同构) 。

不幸的是, 判断两个图是否同构是一件困难的事情。在两个带有 n 个顶点的图的顶点集之间有n! 种可能的一一对应。若 n 太大, 则通过检验每一种对应来看它是否保持相邻关系和不相邻关系, 这样做是不可行的, 是一个 NP 难问题。也就是说, 至今尚没有一种简单而有效地判断图的同构的方法( 即充分必要条件) , 这是图论中的一个重要难题。

一些定义

0-1同化矩阵

rcxd( i, j)

rcad( i, j)

行码距异或矩阵

行码距同或矩阵

行- 行置换

定理和推论

• 定理 1 设无向图 (G=(V, E)) , 邻接矩阵的行列初等变换不改变行码距异或矩阵/行码距同或矩阵中各元素的值, 只是对行码距异或矩阵/行码距同或矩阵做同样的行列初等变换。
• 定理 2 若两个无向图 (G=( V_1, E_1))和(H=( V_2, E_2))同构, 则经过一系列行列初等变换后, 图 G 的邻接矩阵与图 H 的邻接矩阵相等; 图 G 的行码距异或矩阵与图 H 的行码距异或矩阵相等; 图 G 的行码距同或矩阵与图 H 的行码距同或矩阵相等。
• 定理 3 设两个无向图(G=( V_1, E_1))和(H=( V_2, E_2)) , 图 G 和H 同构, 当且仅当, 图 G 的邻接矩阵、行码距异或矩阵、行码距同或矩阵分别与图 H 的邻接矩阵、行码距异或矩阵、行码距同或矩阵具有同一的行-行置换。

推论 1 若下述四个条件中之一成立, 则无向图(G=( V_1, E_1))和(H=( V_2, E_2))不同构。

1. 图 G 的行码距异或矩阵中上三角形部分( 含主对角线上的元素) 中的所有元素之和, 不等于图 H的行码距异或矩阵中上三角形部分 ( 含主对角线上的元素) 中的所有元素之和;
2. 图 G 的行码距异或矩阵中上三角形部分( 含主对角线上的元素) 中的所有元素立方之和, 不等于图 H 的行码距异或矩阵中上三角形部分( 含主对角线上的元素) 中的所有元素立方之和;
3. 图 G 的行码距同或矩阵中上三角形部分( 含主对角线上的元素) 中的所有元素之和, 不等于图 H 的行码距同或矩阵中上三角形部分( 含主对角线上的元素) 中的所有元素之和;
4. 图 G 的行码距同或矩阵中上三角形部分( 含主对角线上的元素) 中的所有元素立方之和, 不等于图 H 的行码距同或矩阵中上三角形部分( 含主对角线上的元素) 中的所有元素立方之和。

算法流程

1. 计算行码距异或/同或矩阵
2. 计算邻接矩阵/行码距异或矩阵/行码距同或矩阵的行- 行置换
3. 计算邻接矩阵/行码距异或矩阵/行码距同或矩阵的行列初等变换

计算行码距异或/同或矩阵

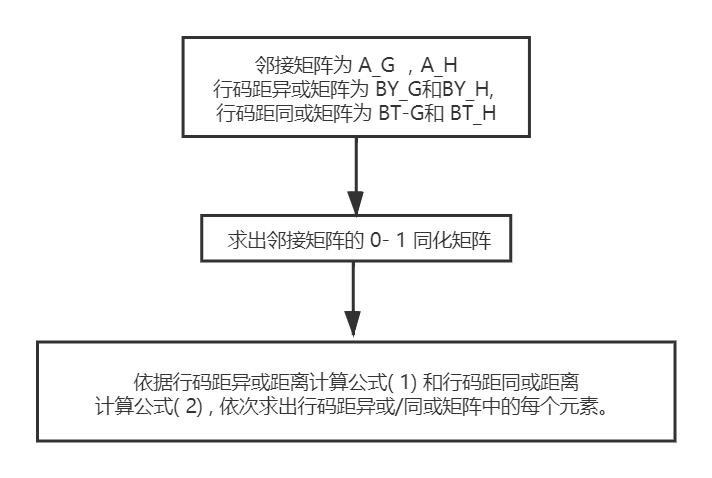
计算邻接矩阵/行码距异或矩阵/行码距同或矩阵的行- 行置换

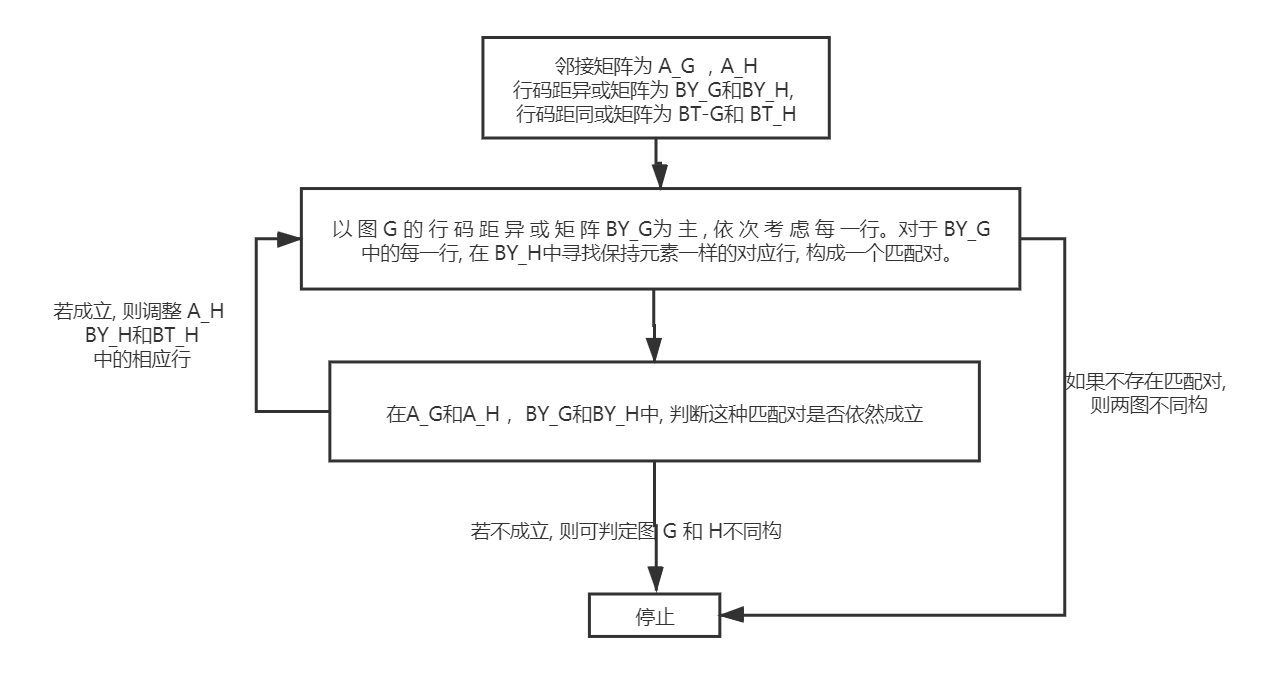
计算邻接矩阵/行码距异或矩阵/行码距同或矩阵的行列初等变换

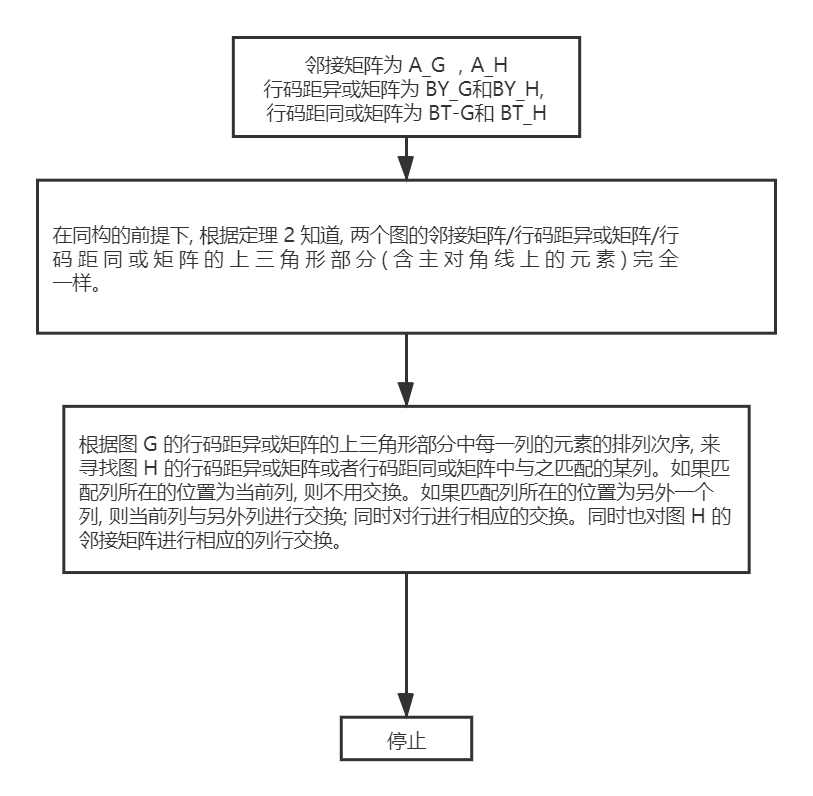
应用举例

图 (G=( V_1, E_1))和(H=( V_2, E_2)); 具体的图形如下所示:

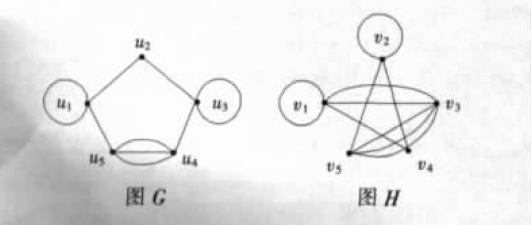
求矩阵

图 G 的邻接矩阵、0- 1 同化矩阵、行码距异或矩阵、行码距同或矩阵如下:

图 H 的邻接矩阵、0- 1 同化矩阵、行码距异或矩阵、行码距同或矩阵如下：

寻找行-行置换

1. 处理 (BY_G)中第 (u_1)行( 1, 3, 5, 4, 5) , 在 (BY_H)中寻找元素一样的行, 找到第 (v_2)行( 5, 1, 4, 3, 5) ; 在 (BY_H、A_H、BT_H)中交换第 (v_1)行和第 (v_2)行, 以及第 (v_1)列和第 (v_2)列。初等变换后如 (BY_H^{(1)})所示。

2. 处理 (BY_G)中第 (u_2)行( 3, 0, 4, 4, 4) , 在 (BY_H)中寻找元素一样的行, 找到第 (v_4)行(3, 4, 4, 0, 4) ; 在 (BY_H、A_H、BT_H)中交换第 (v_2)行和第 (v_4)行, 以及第 (v_2)列和第 (v_4)列。初等变换后如 (BY_H^{(2)})所示。

3. 处理 (BY_G)中第 (u_3)行( 5, 4, 1, 6, 3) , 在 (BY_H)中寻找元素一样的行, 找到第 (v_1)行(5, 4, 6, 1, 3) ; 在 (BY_H、A_H、BT_H)中交换第 (v_3)行和第 (v_1)行, 以及第 (v_3)列和第 (v_1)列。初等变换后如 (BY_H^{(3)})所示。

4. 处理 (BY_G)中第 (u_4)行( 4, 4, 6, 0, 9) , 在 (BY_H)中寻找元素一样的行, 找到第 (v_3)行( 4, 4, 6, 0, 9) ; 在 (BY_H、A_H、BT_H)中不进行行- 行交换, 以及列- 列交换。

5. 处理 (BY_G)中第 (u_5)行( 5, 4, 3, 9, 0) , 在 (BY_H)中寻找元素一样的行, 找到第 (v_5)行( 5, 4, 3, 9, 0) ; 在 (BY_H、A_H、BT_H)中不进行行- 行交换, 以及列- 列交换。
   

6. 得到图 G 的邻接矩阵 (A_G)、行码距异或矩阵 (BY_G)、行码距同或矩阵 (BT_G)分别与图 H 的邻接矩阵 (A_H)、行码距异或矩阵(BY_H)、行码距同或矩阵 (BT_H)之间同一的行- 行置换:
   

邻接矩阵、行码距异或矩阵、行码距同或矩阵初等变换

1. 处理 (BY_G)中上三角形部分( 含主对角线上的元素) 第 (u_1)列, $V_G^T = (1)^T, V_H^T = (1)^T $; 两者相同, 不进行变换。

2. 处理 (BY_G)中上三角形部分( 含主对角线上的元素) 第 (u_2)列, $V_G^T = (3, 0)^T, V_H^T = (3, 0)^T $; 两者相同, 不进行变换。

3. 处理 (BY_G)中上三角形部分( 含主对角线上的元素) 第 (u_3)列, $V_G^T = (5, 4, 1)^T, V_H^T = (5, 4, 1)^T $; 两者相同, 不进行变换。

4. 处理 (BY_G)中上三角形部分( 含主对角线上的元素) 第 (u_4)列, $V_G^T = (4, 4, 6, 0)^T, V_H^T = (4, 4, 6, 0)^T $; 两者相同, 不进行变换。

5. 处理 (BY_G)中上三角形部分( 含主对角线上的元素) 第 (u_5)列, $V_G^T = (5, 4, 3, 9, 0)^T, V_H^T = (5, 4, 3, 9, 0)^T $; 两者相同, 不进行变换。
   

6. 得到同构函数 $$F= (u_1 leftrightarrow v_2, u_2 leftrightarrow v_4, u_3 leftrightarrow v_1, u_4 leftrightarrow v_3, u_5 leftrightarrow v_5)$$
   

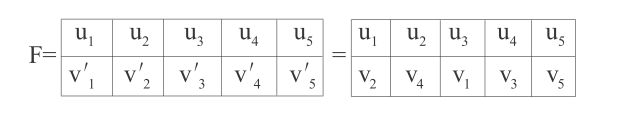
7. 变换后图 H 的图形如下所示:
   

总结

本文提出了行码距异或距离、行码距同或距离、行码距异或矩阵、行码距同或矩阵等新的概念。在此基础上, 找到了依据两个图的邻接矩阵、行码距异或矩阵、行码距同或矩阵是否存在一个同一的行- 行置换来判定图同构的充分必要条件。为了有效地进行矩阵的行列初等变换,提出了依据行码距异或矩阵和行码距同或矩阵的上三角形部分的列行匹配及交换, 来对邻接矩阵进行行列初等变换的思想。在这些思想的指导下, 提出了三个算法( 行码距异或/同或矩阵的计算算法; 邻接矩阵/行码距异或矩阵/行码距同或矩阵的行- 行置换算法; 邻接矩阵/行码距异或矩阵/行码距同或矩阵的行列初等变换算法) , 并对算法进行了算法分析, 得出运行时间为 (O(n^3)) 。