[Luogu1650] 田忌赛马

Description

我国历史上有个著名的故事： 那是在2300年以前。齐国的大将军田忌喜欢赛马。他经常和齐王赛马。他和齐王都有三匹马：常规马，上级马，超级马。一共赛三局，每局的胜者可以从负者这里取得200银币。每匹马只能用一次。齐王的马好，同等级的马，齐王的总是比田忌的要好一点。于是每次和齐王赛马，田忌总会输600银币。

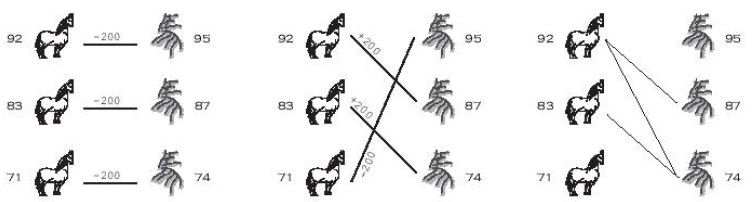
田忌很沮丧，直到他遇到了著名的军师――孙膑。田忌采用了孙膑的计策之后，三场比赛下来，轻松而优雅地赢了齐王200银币。这实在是个很简单的计策。由于齐王总是先出最好的马，再出次好的，所以田忌用常规马对齐王的超级马，用自己的超级马对齐王的上级马，用自己的上级马对齐王的常规马，以两胜一负的战绩赢得200银币。实在很简单。

如果不止三匹马怎么办？这个问题很显然可以转化成一个二分图最佳匹配的问题。把田忌的马放左边，把齐王的马放右边。田忌的马A和齐王的B之间，如果田忌的马胜，则连一条权为200的边；如果平局，则连一条权为0的边；如果输，则连一条权为－200的边……如果你不会求最佳匹配，用最小费用最大流也可以啊。 然而，赛马问题是一种特殊的二分图最佳匹配的问题，上面的算法过于先进了，简直是杀鸡用牛刀。现在，就请你设计一个简单的算法解决这个问题。

Input

第一行一个整数n，表示他们各有几匹马（两人拥有的马的数目相同）。第二行n个整数，每个整数都代表田忌的某匹马的速度值(0 <= 速度值<= 100)。第三行n个整数，描述齐王的马的速度值。两马相遇，根据速度值的大小就可以知道哪匹马会胜出。如果速度值相同，则和局，谁也不拿钱。

Output

仅一行，一个整数，表示田忌最大能得到多少银币。

Sample Input

3
92 83 71
95 87 74

Sample Output

200

Hint

对于20%的数据，1<=N<=65；

对于40%的数据，1<=N<=250；

对于100%的数据，1<=N<=2000。

(DP)

设f[i][j]表示齐王按从强到弱的顺序出马和田忌进行了i场比赛之后，从"头"取了j匹较强的马，从"尾"取了i-j匹较弱的马，所能获得的最大盈利。

则状态转移方程为:f[i][j]=max(f[i-1][j]+g[n-(i-j)+1][i],f[i-1][j-1]+g[j][i]；
其中g[i][j]表示田忌的马和齐王的马分别按照由强到弱的顺序排序之后，田忌的第i匹马和齐王的第j匹马赛跑所能取得的盈利，胜为 200，负为 -200，平为0。

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int N=2001,INF=-2e+8;
int a[N],b[N],g[N][N],f[N][N];

bool Cmp(int n1,int n2) {return n1>n2;}

int main()
{
	int n,Ans,i,j; scanf("%d",&n);
	for (i=1;i<=n;++i) scanf("%d",&a[i]);
	for (i=1;i<=n;++i) scanf("%d",&b[i]);
	sort(a+1,a+n+1,Cmp),sort(b+1,b+n+1,Cmp);
	for (i=1;i<=n;++i)
		for (j=1;j<=n;++j)
		{
			if (a[i]>b[j]) g[i][j]=200;
			else if (a[i]==b[j]) g[i][j]=0;
				 else g[i][j]=-200;
			f[i][j]=INF;
		}
	for (i=1;i<=n;++i)
	{
		f[i][0]=f[i-1][0]+g[n-i+1][i];
		f[i][i]=f[i-1][i-1]+g[i][i];
		for (j=1;j<i;++j)
			f[i][j]=max(f[i-1][j]+g[n-i+j+1][i],f[i-1][j-1]+g[j][i]);
	}
	Ans=f[n][1];
	for (i=2;i<=n;++i) Ans=max(Ans,f[n][i]);
	printf("%d
",Ans);
	return 0;
}

优化内存：

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int N=2001,INF=-2e+8;
int a[N],b[N],g[N][N],f[N];

bool Cmp(int n1,int n2) {return n1>n2;}

int main()
{
    int n,Ans,i,j; scanf("%d",&n);
    for (i=1;i<=n;++i) scanf("%d",&a[i]);
    for (i=1;i<=n;++i) scanf("%d",&b[i]);
    sort(a+1,a+n+1,Cmp),sort(b+1,b+n+1,Cmp);
    for (i=1;i<=n;++i)
        for (j=1;j<=n;++j)
        {
            if (a[i]>b[j]) g[i][j]=200;
            else if (a[i]==b[j]) g[i][j]=0;
                 else g[i][j]=-200;
        }
    for (i=1;i<=n;++i) f[i]=INF;
    for (i=1;i<=n;++i)
    {
        f[i]=f[i-1]+g[i][i];
        for (j=i-1;j>0;--j)
            f[j]=max(f[j]+g[n-i+j+1][i],f[j-1]+g[j][i]);
        f[0]=f[0]+g[n-i+1][i];
    }
    Ans=f[1];
    for (i=2;i<=n;++i) Ans=max(Ans,f[i]);
    printf("%d
",Ans);
    return 0;
}

(~)

---

用f[i][j]表示田忌出动速度排名在前i的马，齐王出动速度排名在前j的马后，田忌所能取得的最大利润，则应分以下三种情况讨论：
1. 若田忌的第i匹马比齐王的第j匹马快，则f[i][j]=max{f[i-1][j-1]+200 ,max(f[i-1][j],f[i][j-1])-200}
2. 若田忌的第i匹马和齐王的第j匹马相等，则f[i][j]=max{f[i-1][j-1],max(f[i-1][j],f[i][j-1])-200}
3. 若田忌的第(i)匹马比齐王的第j匹马慢，则f[i][j]=max{f[i-1][j],f[i][j-1]}-200

数据帮助理解，模拟程序过程：(第一列为田忌的马的速度，第一行为齐王的马的速度)

     6    3   2
5 -200  200 200 
3 -200    0 400 
1 -200 -200 200 

(~)

     6    3   2
6    0  200 200 
3 -200    0 400 
1 -200 -200 200 

(~)

     6   3    2
6    0 200  200 
3 -200   0  400 
2 -200 -200 200 

(~)

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int N=2001;
int a[N],b[N],dp[N][N];

bool Cmp(int x,int y) {return x>y;}

int main()
{
	int n,i,j; scanf("%d",&n);
	for (i=1;i<=n;++i) scanf("%d",&a[i]);
	for (i=1;i<=n;++i) scanf("%d",&b[i]);
	sort(a+1,a+n+1,Cmp),sort(b+1,b+n+1,Cmp);
	for (i=1;i<=n;++i)
		for (j=1;j<=n;++j)
			if (a[i]>b[j]) dp[i][j]=max(dp[i-1][j-1]+200,max(dp[i-1][j]-200,dp[i][j-1]-200));
			else if (a[i]==b[j]) dp[i][j]=max(dp[i-1][j-1],max(dp[i-1][j]-200,dp[i][j-1]-200));
				 else dp[i][j]=max(dp[i-1][j]-200,dp[i][j-1]-200);
	printf("%d
",dp[n][n]);
	return 0;
}

贪心

分以下三种情况考虑：

• 如果田忌目前的最快马快于齐王目前的最快马，则两者比

• 如果田忌的最快马慢于齐王的最快马，则用田忌的最慢马与齐王的最快马比(()减少损失())

• 如果田忌的最快马和齐王的最快马相等，分以下两种情况：

  1. 若田忌的最慢马快与齐王的最慢马，两者比（能赢就赢呗）
  2. 其他，用田忌的最慢马与齐王的最快马比（贡献最大）

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int N=2001;
int a[N],b[N];

void Scanf(int &x)
{
	x=0;
	char s=getchar();
	while(s<'0'||s>'9') s=getchar();
	while(s>='0'&&s<='9') x=x*10+s-'0',s=getchar();
}

int main()
{
	int Ans,n,la,lb,ra,rb,i;
	Scanf(n);
	for (i=1;i<=n;++i) Scanf(a[i]);
	for (i=1;i<=n;++i) Scanf(b[i]);
	sort(a+1,a+n+1),sort(b+1,b+n+1);
	Ans=0,la=lb=1,ra=rb=n;
	for (i=1;i<=n;++i)
	{
		if (a[ra]>b[rb]) Ans+=200,--ra,--rb;
		else if (a[ra]<b[rb]) Ans-=200,++la,--rb;
			 else if (a[la]>b[lb]) Ans+=200,++la,++lb;
			 	  else
			 	  {
			 	  	if (a[la]<b[rb]) Ans-=200;
			 	  	++la,--rb;
		 		  }
	}
	printf("%d
",Ans);
	return 0;
}