[Luogu1325] 雷达安装

Description

假设海岸线是一条无限延伸的直线。它的一侧是陆地，另一侧是海洋。每一座小岛是在海面上的一个点。雷达必须安装在陆地上（包括海岸线），并且每个雷达都有相同的扫描范围d。你的任务是建立尽量少的雷达站，使所有小岛都在扫描范围之内。

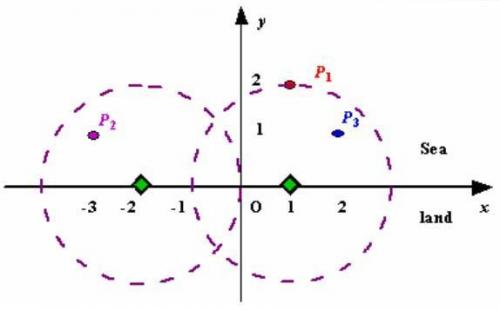
数据使用笛卡尔坐标系，定义海岸线为x轴。在x轴上方为海洋，下方为陆地。

样例1如图所示

Input

第一行包括2个整数n和d，n是岛屿数目，d是雷达扫描范围。

接下来n行为岛屿坐标。

Output

一个整数表示最少需要的雷达数目，若不可能覆盖所有岛屿，输出“-1”。

Sample Input

3 2
1 2
-3 1
2 1

Sample Output

2

Hint

(n le 1000),(d le 20000)

(| x_i | le 2 imes 10^6),(0 le y_i le 20000)

题解

• 题目中说雷达必须安装在陆地上（包括海岸线），实际上就是说雷达站必须要建在海岸线上

• 雷达的探测距离为(d)，所以雷达想要覆盖岛屿，就必须和岛屿的距离不超过(d)

• 雷达的建设又有一个活动区间([x-sqrt(d imes d-y imes y),x+sqrt(d imes d+y imes y)])

• 从以上分析可以看出：本题实际上是一个区间取点问题，算法为贪心

因此我们可以先求出每个岛屿能够覆盖的左端点和右端点，再按区间的右端点从小到大排序，依次处理每一个区间。

1. 如果该区间的左端点已在选定点的范围内，移动至下一个区间；
2. 否则，个数加(1)，选择该区间的右端点处建一个雷达。

代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;

const int N=1200;
struct node{double b,e;}ld[N];

bool Cmp(const node &num1,const node &num2) {return num1.e<num2.e;}

inline void Scanf(int &num1,int &num2)
{
	int f=1; num1=num2=0;
	char s=getchar();
	while(s<'0'||s>'9')
	{
		if(s=='-') f=-1;
		s=getchar();
	}
	while(s>='0'&&s<='9') num1=num1*10+s-'0',s=getchar();
	num1*=f;
	f=1;
	while(s<'0'||s>'9')
	{
		if(s=='-') f=-1;
		s=getchar();
	}
	while(s>='0'&&s<='9') num2=num2*10+s-'0',s=getchar();
	num2*=f;
}

int main()
{
	int n,d,d2,x,y,Ans=1,i; double Res;
	Scanf(n,d); d2=d*d;
	for (i=1;i<=n;++i)
	{
		Scanf(x,y);
		if (y>d) {printf("-1
");goto end;}
		else Res=sqrt(d2-y*y),ld[i].b=x-Res,ld[i].e=x+Res;
	}
	sort(ld+1,ld+n+1,Cmp);
	Res=ld[1].e;
	for (i=2;i<=n;++i)
		if (Res<ld[i].b) ++Ans,Res=ld[i].e;
	printf("%d
",Ans);
	end:
	return 0;
}