Description
Let's play a card game called Gap.
You have 28 cards labeled with two-digit numbers. The first digit (from 1 to 4) represents the suit of the card, and the second digit (from 1 to 7) represents the value of the card.
First, you shu2e the cards and lay them face up on the table in four rows of seven cards, leaving a space of one card at the extreme left of each row. The following shows an example of initial layout.
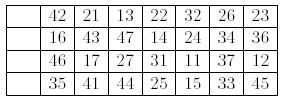
Next, you remove all cards of value 1, and put them in the open space at the left end of the rows: "11" to the top row, "21" to the next, and so on.
Now you have 28 cards and four spaces, called gaps, in four rows and eight columns. You start moving cards from this layout.
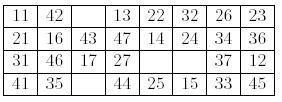
At each move, you choose one of the four gaps and fill it with the successor of the left neighbor of the gap. The successor of a card is the next card in the same suit, when it exists. For instance the successor of "42" is "43", and "27" has no successor.
In the above layout, you can move "43" to the gap at the right of "42", or "36" to the gap at the right of "35". If you move "43", a new gap is generated to the right of "16". You cannot move any card to the right of a card of value 7, nor to the right of a gap.
The goal of the game is, by choosing clever moves, to make four ascending sequences of the same suit, as follows.
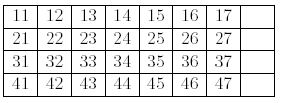
Your task is to find the minimum number of moves to reach the goal layout.
Input
The input starts with a line containing the number of initial layouts that follow.
Each layout consists of five lines - a blank line and four lines which represent initial layouts of four rows. Each row has seven two-digit numbers which correspond to the cards.
Output
For each initial layout, produce a line with the minimum number of moves to reach the goal layout. Note that this number should not include the initial four moves of the cards of value 1. If there is no move sequence from the initial layout to the goal layout, produce "-1".
Sample Input
4
12 13 14 15 16 17 21
22 23 24 25 26 27 31
32 33 34 35 36 37 41
42 43 44 45 46 47 11
26 31 13 44 21 24 42
17 45 23 25 41 36 11
46 34 14 12 37 32 47
16 43 27 35 22 33 15
17 12 16 13 15 14 11
27 22 26 23 25 24 21
37 32 36 33 35 34 31
47 42 46 43 45 44 41
27 14 22 35 32 46 33
13 17 36 24 44 21 15
43 16 45 47 23 11 26
25 37 41 34 42 12 31
Sample Output
0
33
60
-1
Source
Japan 2003,Aizu
题解
这题的关键在于读懂题目,这里不提供题意。
开始正文:由于这题要求求最小步数,所以我们最好用(BFS),再加上(32)的数据以不允许我们定义简单的(bool)数组,因此我是用的(Hash)记录状态,先解释一下定义:
const int Mod=131,maxm=200007;
struct node
{
int num[50],kong[5],id[50],ans,nx;
}Hash[maxm];
int hd[maxm];
(Hash[])记录状态,关于题目中的矩阵的存放,我用的是化二维为一维,其中的(num[])记录的是矩阵,(kong[])记录每一个空格在矩阵中的位置,同样该位置也是一个数,(id[])记录每一个数(-10)后在矩阵中的位置,至于(-10),那是为了节约空间,(ans)记录移动到该步骤所需要的步数,(nx)指向与该状态相同(Hash)值的状态在(Hash[])中的下标
接下来的一部分代码是在计算(Hash)值:
int GetHash(int tmp[])
{
long long Res=0;
for(int i=0;i<32;++i)
Res=Res*Mod+tmp[i],Res&=0xFFFFFF;
return Res%maxm;
}
插入操作:
void Insert(int tmp[],int id)
{
int hashnum=GetHash(tmp);
Hash[id].nx=hd[hashnum],hd[hashnum]=id;
}
判断是否与以前状态相同,同(1),异(0):
bool Check(int tmpa[],int tmpb[])
{
for(int i=0;i<32;++i)
if(tmpa[i]!=tmpb[i]) return 0;
return 1;
}
查找,若有返回位置,若没有返回(-1):
int Find(int tmp[])
{
int hashnum=GetHash(tmp);
for(int i=hd[hashnum];i!=-1;i=Hash[i].nx)
if(Check(tmp,Hash[i].num)) return i;
return -1;
}
PS:位置为(0)则代表它是目标状态。
(BFS):
int Bfs()
{
int l,r,tmp,YH,tmp1;
node t;
l=0,r=1;
while(l<r)
{
++l;
for(int i=1;i<=4;++i)
{
t=Hash[l] , tmp=Hash[l].kong[i],
YH=Hash[l].num[tmp-1];
if((YH%10<7)&&(YH%10>0))
{
t.num[tmp]=YH+1,//移动
tmp1=Hash[l].id[YH+1] , t.num[tmp1]=0,//移动
t.kong[i]=tmp1,//移动
t.id[YH+1]=tmp,//移动
t.ans=Hash[l].ans+1;//移动
YH=Find(t.num);
if(!YH) return t.ans;
if(YH==-1)
{
++r,Hash[r]=t;
Insert(t.num,r);
}
}
}
}
return -1;
}
(main)与预处理:
int main()
{
int T;
for(int i=0;i<4;++i)
for(int j=0;j<7;++j) Hash[0].num[i*8+j]=i*10+j+1;
int YH,numK;
for(scanf("%d",&T);T;--T)
{
memset(hd,-1,sizeof(hd));
Insert(Hash[0].num,0);
numK=0;
Hash[1].ans=0;
for(int i=0;i<4;++i)
{
Hash[1].num[i*8]=i*10+1;
for(int j=1;j<=7;++j)
{
scanf("%d",&YH);
if(YH==11||YH==21||YH==31||YH==41)
Hash[1].num[i*8+j]=0,
Hash[1].kong[++numK]=i*8+j;
else
Hash[1].num[i*8+j]=YH-10,
Hash[1].id[YH-10]=i*8+j;
}
}
if(!Find(Hash[1].num)) {puts("0"); continue;}
Insert(Hash[1].num,1),
printf("%d
",Bfs());
}
return 0;
}
(my~code)
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<set>
#include<bitset>
#include<map>
#include<vector>
using namespace std;
const int Mod=131,maxm=200007;
struct node
{
int num[50],kong[5],id[50],ans,nx;
}Hash[maxm];
int hd[maxm];
int GetHash(int tmp[])
{
long long Res=0;
for(int i=0;i<32;++i)
Res=Res*Mod+tmp[i],Res&=0xFFFFFF;
return Res%maxm;
}
void Insert(int tmp[],int id)
{
int hashnum=GetHash(tmp);
Hash[id].nx=hd[hashnum],hd[hashnum]=id;
}
bool Check(int tmpa[],int tmpb[])
{
for(int i=0;i<32;++i)
if(tmpa[i]!=tmpb[i]) return 0;
return 1;
}
int Find(int tmp[])
{
int hashnum=GetHash(tmp);
for(int i=hd[hashnum];i!=-1;i=Hash[i].nx)
if(Check(tmp,Hash[i].num)) return i;
return -1;
}
int Bfs()
{
int l,r,tmp,YH,tmp1;
node t;
l=0,r=1;
while(l<r)
{
++l;
for(int i=1;i<=4;++i)
{
t=Hash[l] , tmp=Hash[l].kong[i],
YH=Hash[l].num[tmp-1];
if((YH%10<7)&&(YH%10>0))
{
t.num[tmp]=YH+1,
tmp1=Hash[l].id[YH+1] , t.num[tmp1]=0,
t.kong[i]=tmp1,
t.id[YH+1]=tmp,
t.ans=Hash[l].ans+1;
YH=Find(t.num);
if(!YH) return t.ans;
if(YH==-1)
{
++r,Hash[r]=t;
Insert(t.num,r);
}
}
}
}
return -1;
}
int main()
{
int T;
for(int i=0;i<4;++i)
for(int j=0;j<7;++j) Hash[0].num[i*8+j]=i*10+j+1;
int YH,numK;
for(scanf("%d",&T);T;--T)
{
memset(hd,-1,sizeof(hd));
Insert(Hash[0].num,0);
numK=0;
Hash[1].ans=0;
for(int i=0;i<4;++i)
{
Hash[1].num[i*8]=i*10+1;
for(int j=1;j<=7;++j)
{
scanf("%d",&YH);
if(YH==11||YH==21||YH==31||YH==41)
Hash[1].num[i*8+j]=0,
Hash[1].kong[++numK]=i*8+j;
else
Hash[1].num[i*8+j]=YH-10,
Hash[1].id[YH-10]=i*8+j;
}
}
if(!Find(Hash[1].num)) {puts("0"); continue;}
Insert(Hash[1].num,1),
printf("%d
",Bfs());
}
return 0;
}