小波学习之二（单层一维离散小波变换DWT的Mallat算法C++实现优化）--转载

小波学习之二（单层一维离散小波变换DWT的Mallat算法C++实现优化）

 

        在上回《小波学习之一》中，已经详细介绍了Mallat算法C++实现，效果还可以，但也存在一些问题，比如，代码难于理解，同时出现了边界问题。在此，本文将重构代码，采用新的方法解决这些问题，同时也加深对小波变换的理解。

        MATLAB作为经典的数学工具，分析其小波变换dwt和idwt实现后发现真的很经典，学习参考价值很高。下面结合南京理工大学 谭彩铭的《解读matlab之小波库函数》及MATLAB小波工具包中m文件的情况，作一个小结，最后用C++函数进行实现，并且编译调试OK。
        一、MATLAB上dwt函数的工作过程
        假设x=[x(1) x(2) x(3) x(4) x(5) x(6) x(7)]，计算y=dwt(x,’db2’)，其计算过程主要由三个部分组成：
1、边缘延拓，它主要由函数wextend完成。

仔细分析子程序部分，函数wextend的用法为y=wextend('1D','sym',x,3)；这样得到的y=[ x(3) x(2) x(1) x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(7) x(6) x(5)]
2、卷积运算，它主要由函数conv2完成。
仔细分析子程序部分，核心语句有z=conv2(y,Lo_D,'valid')；这里设Lo_D=[h(1) h(2) h(3) h(4)]。

这2步的实现过程示意图如下：

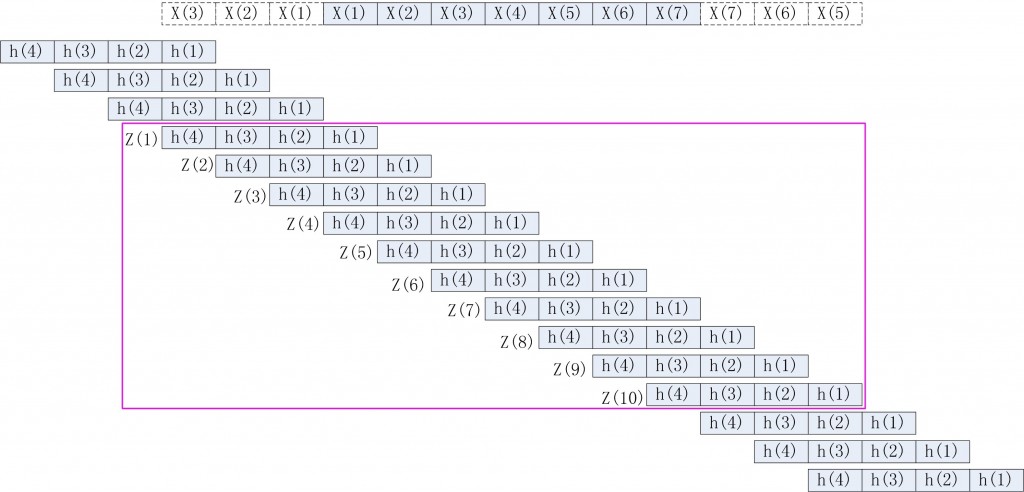
3、最后就是下采样即隔点采样，其下采样是按照式a = z(2:2:length(z))进行的，高频低频部分均如此，项数为floor（(7+4-1)/2）。

最后的dwt低频系数结果是[z(2) z(4) z(6) z(8) z(10)]，高频系数求解过程和低频系数一样，在此不再赘述。

        二、MATLAB上idwt函数的工作过程

1、上采样即隔点插0，dyadup(x,0)。

2、卷积运算，它也是最终由函数conv2完成。

3、抽取结果，wkeep1(x,s,'c')。

下面啥都不说show核心代码实现，欢迎讨论。

/**
 * @brief 边缘延拓
 * @param typeId 延拓数据的类型，1D or 2D
 * @param modeId 延拓方式：对称、周期
 * @param in 输入数据
 * @param inLen 输入数据的长度
 * @param filterLen 小波基滤波器长度
 * @param out 返回结果数组
 * @return 返回结果数组长度
 */
int SignalExtension(int typeId,
        int modeId,
        double *in,
        int inLen,
        int filterLen,
        double out[])
{
    if((NULL == in)||(NULL == out))
        return -1;
    if(0 != typeId) // 目前只支持一种模型
        return -1;
    //if(0 != modeId) // 目前只支持一种模型，信号对称拓延  'sym' or 'symh'      Symmetric-padding (half-point): boundary value symmetric replication
    //  return -1;
    if( inLen < filterLen ) // inLen should lager than or equal extendLen, otherwise no extension
        return -1;

    int i;
    int extendLen = filterLen - 1;

    if(0 == modeId) // 信号对称拓延
    {
        for(i=0; i<inLen; i++)
        {
            out[extendLen+i] = in[i];
        }
        for(i=0; i<extendLen; i++)
        {
            out[i]                     = out[2*extendLen - i - 1];       // 左边沿对称延拓
            out[inLen + extendLen + i] = out[extendLen + inLen - i - 1]; // 右边沿对称延拓
        }

        return inLen + 2*extendLen;
    }
    else if(1 == modeId) // 信号周期拓延
    {
        for( i = 0; i < extendLen; i++ )
            out[i] = in[inLen-extendLen+i];
        for ( i = 0; i < inLen; i++ )
            out[extendLen+i] = in[i];

        return inLen + extendLen;
    }

}

/**
 * @brief 边缘延拓
 * @param typeId 延拓数据的类型，1D or 2D
 * @param modeId 延拓方式：对称、周期
 * @param in 输入数据
 * @param inLen 输入数据的长度
 * @param filterLen 小波基滤波器长度
 * @param out 返回结果数组
 * @return 返回结果数组长度
 */
int SignalExtension(int typeId,
		int modeId,   
		double *in,   
		int inLen,    
		int filterLen, 
		double out[])  
{
    if((NULL == in)||(NULL == out))
        return -1;
    if(0 != typeId) // 目前只支持一种模型
    	return -1;
    //if(0 != modeId) // 目前只支持一种模型，信号对称拓延  'sym' or 'symh'  	Symmetric-padding (half-point): boundary value symmetric replication
    //	return -1;
    if( inLen < filterLen ) // inLen should lager than or equal extendLen, otherwise no extension
    	return -1;

    int i;
    int extendLen = filterLen - 1;

    if(0 == modeId) // 信号对称拓延
    {
        for(i=0; i<inLen; i++)
        {
        	out[extendLen+i] = in[i];
        }
        for(i=0; i<extendLen; i++)
        {
        	out[i]                     = out[2*extendLen - i - 1];       // 左边沿对称延拓
        	out[inLen + extendLen + i] = out[extendLen + inLen - i - 1]; // 右边沿对称延拓
        }

        return inLen + 2*extendLen;
    }
    else if(1 == modeId) // 信号周期拓延
    {
		for( i = 0; i < extendLen; i++ )
			out[i] = in[inLen-extendLen+i];
		for ( i = 0; i < inLen; i++ )
			out[extendLen+i] = in[i];

        return inLen + extendLen;
    }

}

/**
 * @brief 上采样  隔点插0
 * @param data 输入数据指针
 * @param n 输入数据长度
 * @param result 返回结果数组
 * @return 返回结果数组长度
 */
int Upsampling(double* data, int n, double result[])
{
    int i;

    for( i = 0; i < n; i++ )
    {
        result[2*i] = data[i];
        result[2*i+1] = 0;
    }

    return( 2*n );
}

/**
 * @brief 上采样  隔点插0
 * @param data 输入数据指针
 * @param n 输入数据长度
 * @param result 返回结果数组
 * @return 返回结果数组长度
 */
int Upsampling(double* data, int n, double result[])
{
	int i;

	for( i = 0; i < n; i++ )
	{
		result[2*i] = data[i];
		result[2*i+1] = 0;
	}

	return( 2*n );
}

/**
 * @brief 下采样  隔点采样
 * @param data 输入数据指针
 * @param n 输入数据长度
 * @param result 返回结果数组
 * @return 返回结果数组长度
 */
int Downsampling(double* data, int n, double result[])
{
    int i, m;

    m = n/2;
    for( i = 0; i < m; i++ )
        result[i] = data[i*2 + 1];

    return( m );
}

/**
 * @brief 下采样  隔点采样
 * @param data 输入数据指针
 * @param n 输入数据长度
 * @param result 返回结果数组
 * @return 返回结果数组长度
 */
int Downsampling(double* data, int n, double result[])
{
	int i, m;

	m = n/2;
	for( i = 0; i < m; i++ )
		result[i] = data[i*2 + 1];

	return( m );
}

/**
 * @brief 卷积运算
 * @param shapeId 卷积结果处理方式
 * @param double *inSignal, int signalLen, // 输入信号及其长度
 * @param double *inFilter, int filterLen, // 输入滤波器及其长度
 * @param double outConv[], int *convLen)   // 输出卷积结果及其长度
 * @return
 */
void Conv1(int shapeId,                  // 卷积结果处理方式
        double *inSignal, int signalLen, // 输入信号及其长度
        double *inFilter, int filterLen, // 输入滤波器及其长度
        double outConv[], int *convLen)   // 输出卷积结果及其长度
{
    if((NULL == inSignal)||(NULL == inFilter)||(NULL == outConv))
        return;

    int n,k,kmin,kmax,p;
    if(0 == shapeId)      // 对于MATLAB conv(...,'shape')  -----full
    {
        *convLen = signalLen + filterLen - 1;
        for (n = 0; n < *convLen; n++)
        {
            outConv[n] = 0;

            kmin = (n >= filterLen - 1) ? n - (filterLen - 1) : 0;
            kmax = (n < signalLen - 1) ? n : signalLen - 1;

            for (k = kmin; k <= kmax; k++)
            {
                outConv[n] += inSignal[k] * inFilter[n - k];
            }
        }
    }
    else if(1 == shapeId) // 对于MATLAB conv(...,'shape')  -----valid
    {
        *convLen = signalLen - filterLen + 1;
        for (n = filterLen - 1; n < signalLen; n++)
        {
            p = n - filterLen + 1;
            outConv[p] = 0;

            kmin = (n >= filterLen - 1) ? n - (filterLen - 1) : 0;
            kmax = (n < signalLen - 1) ? n : signalLen - 1;

            for (k = kmin; k <= kmax; k++)
            {
                outConv[p] += inSignal[k] * inFilter[n - k];
            }
        }
    }
    else
        return ;

}

/**
 * @brief 卷积运算
 * @param shapeId 卷积结果处理方式
 * @param double *inSignal, int signalLen, // 输入信号及其长度
 * @param double *inFilter, int filterLen, // 输入滤波器及其长度
 * @param double outConv[], int *convLen)   // 输出卷积结果及其长度
 * @return
 */
void Conv1(int shapeId,                  // 卷积结果处理方式
		double *inSignal, int signalLen, // 输入信号及其长度
		double *inFilter, int filterLen, // 输入滤波器及其长度
		double outConv[], int *convLen)   // 输出卷积结果及其长度
{
    if((NULL == inSignal)||(NULL == inFilter)||(NULL == outConv))
        return;

    int n,k,kmin,kmax,p;
    if(0 == shapeId)      // 对于MATLAB conv(...,'shape')  -----full
    {
    	*convLen = signalLen + filterLen - 1;
    	for (n = 0; n < *convLen; n++)
    	{
    		outConv[n] = 0;

    	    kmin = (n >= filterLen - 1) ? n - (filterLen - 1) : 0;
    	    kmax = (n < signalLen - 1) ? n : signalLen - 1;

    	    for (k = kmin; k <= kmax; k++)
    	    {
    	    	outConv[n] += inSignal[k] * inFilter[n - k];
    	    }
    	}
    }
    else if(1 == shapeId) // 对于MATLAB conv(...,'shape')  -----valid
    {
    	*convLen = signalLen - filterLen + 1;
    	for (n = filterLen - 1; n < signalLen; n++)
    	{
    		p = n - filterLen + 1;
    		outConv[p] = 0;

    	    kmin = (n >= filterLen - 1) ? n - (filterLen - 1) : 0;
    	    kmax = (n < signalLen - 1) ? n : signalLen - 1;

    	    for (k = kmin; k <= kmax; k++)
    	    {
    	    	outConv[p] += inSignal[k] * inFilter[n - k];
    	    }
    	}
    }
    else
    	return ;

}

/**
 * @brief 小波变换之分解
 * @param sourceData 源数据
 * @param dataLen 源数据长度
 * @param db 过滤器类型
 * @param cA 分解后的近似部分序列-低频部分
 * @param cD 分解后的细节部分序列-高频部分
 * @return 正常则返回分解后序列的数据长度，错误则返回-1
 */
int Wavelet::Decomposition(double* sourceData, int dataLen, Filter db, double* cA, double* cD)
{
    if(dataLen < 2)
        return -1;
    if((NULL == sourceData)||(NULL == cA)||(NULL == cD))
        return -1;

    m_db = db;
    int filterLen = m_db.length;
    int i, n;
    int decLen = (dataLen+filterLen-1)/2;
    int convLen = 0;
    double extendData[dataLen+2*filterLen-2];
    double convDataLow[dataLen+filterLen-1];
    double convDataHigh[dataLen+filterLen-1];

/*
MATLAB上dwt函数的工作过程
假设x=[x(1) x(2) x(3) x(4) x(5) x(6) x(7)],计算y=dwt(x,’db2’)。
其计算过程主要由两个部分组成：
1：边缘延拓，它主要由函数wextend完成。
2：卷积运算，它主要由函数conv2完成。
先看第一部分，仔细分析子程序部分，函数wextend的用法为y=wextend('1D','sym',x,3);
这样得到的y=[ x(3) x(2) x(1) x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(7) x(6) x(5)]
在看第二部分，仔细分析子程序部分，核心语句有z=conv2(y,Lo_D,'valid');
这里设Lo_D=[h(1) h(2) h(3) h(4)]。
3：最后就是下采样，其下采样是按照式a = z(2:2:length(z))进行的，高频低频部分均如此，项数为floor（(7+4-1)/2）。
 */
    // 1.边缘延拓
    SignalExtension(0, 0 , sourceData, dataLen, filterLen, extendData);

    // 2.卷积运算
    Conv1(1, extendData, dataLen+2*filterLen-2, db.lowFilterDec, filterLen, convDataLow, &convLen);
    Conv1(1, extendData, dataLen+2*filterLen-2, db.highFilterDec, filterLen, convDataHigh, &convLen);

    // 3.下采样
    Downsampling(convDataLow, dataLen + filterLen - 1, cA);
    Downsampling(convDataHigh, dataLen + filterLen - 1, cD);

    return decLen;
}

/**
 * @brief 小波变换之分解
 * @param sourceData 源数据
 * @param dataLen 源数据长度
 * @param db 过滤器类型
 * @param cA 分解后的近似部分序列-低频部分
 * @param cD 分解后的细节部分序列-高频部分
 * @return 正常则返回分解后序列的数据长度，错误则返回-1
 */
int Wavelet::Decomposition(double* sourceData, int dataLen, Filter db, double* cA, double* cD)
{
    if(dataLen < 2)
        return -1;
    if((NULL == sourceData)||(NULL == cA)||(NULL == cD))
        return -1;

    m_db = db;
    int filterLen = m_db.length;
    int i, n;
    int decLen = (dataLen+filterLen-1)/2;
    int convLen = 0;
    double extendData[dataLen+2*filterLen-2];
    double convDataLow[dataLen+filterLen-1];
    double convDataHigh[dataLen+filterLen-1];

/*
MATLAB上dwt函数的工作过程
假设x=[x(1) x(2) x(3) x(4) x(5) x(6) x(7)],计算y=dwt(x,’db2’)。
其计算过程主要由两个部分组成：
1：边缘延拓，它主要由函数wextend完成。
2：卷积运算，它主要由函数conv2完成。
先看第一部分，仔细分析子程序部分，函数wextend的用法为y=wextend('1D','sym',x,3);
这样得到的y=[ x(3) x(2) x(1) x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(7) x(6) x(5)]
在看第二部分，仔细分析子程序部分，核心语句有z=conv2(y,Lo_D,'valid');
这里设Lo_D=[h(1) h(2) h(3) h(4)]。
3：最后就是下采样，其下采样是按照式a = z(2:2:length(z))进行的，高频低频部分均如此，项数为floor（(7+4-1)/2）。
 */
    // 1.边缘延拓
    SignalExtension(0, 0 , sourceData, dataLen, filterLen, extendData);

    // 2.卷积运算
    Conv1(1, extendData, dataLen+2*filterLen-2, db.lowFilterDec, filterLen, convDataLow, &convLen);
    Conv1(1, extendData, dataLen+2*filterLen-2, db.highFilterDec, filterLen, convDataHigh, &convLen);

    // 3.下采样
    Downsampling(convDataLow, dataLen + filterLen - 1, cA);
    Downsampling(convDataHigh, dataLen + filterLen - 1, cD);

    return decLen;
}

/**
 * @brief 小波变换之重构
 * @param cA 分解后的近似部分序列-低频部分
 * @param cD 分解后的细节部分序列-高频部分
 * @param cALength 输入数据长度
 * @param RecLength 输入重构后的原始数据长度
 * @param db 过滤器类型
 * @param recData 重构后输出的数据
 * @return 正常则返回重构数据长度，错误则返回-1
 */
int Wavelet::Reconstruction(double *cA, double *cD, int cALength, int RecLength, Filter db, double* recData)
{
    if((NULL == cA)||(NULL == cD)||(NULL == recData))
        return -1;

    m_db = db;
    int filterLen = m_db.length;

    int i,j;
    int n,k,p;
    int recLen = RecLength;

    int convLen = 0;
    double convDataLow[recLen+filterLen-1];
    double convDataHigh[recLen+filterLen-1];

    double cATemp[2*cALength];
    double cDTemp[2*cALength];

    memset(convDataLow, 0, (recLen+filterLen-1)*sizeof(double)); // 清0
    memset(convDataHigh, 0, (recLen+filterLen-1)*sizeof(double)); // 清0
    memset(cATemp, 0, 2*cALength*sizeof(double)); // 清0
    memset(cDTemp, 0, 2*cALength*sizeof(double)); // 清0

    // 1.隔点插0
    Upsampling(cA, cALength, cATemp);
    Upsampling(cD, cALength, cDTemp);

    // 2.卷积运算
    Conv1(0, cATemp, 2*cALength-1, db.lowFilterRec, filterLen ,convDataLow, &convLen);
    convLen = 0;
    Conv1(0, cDTemp, 2*cALength-1, db.highFilterRec, filterLen ,convDataHigh, &convLen);

    // 3.抽取结果及求和——实现类似MATLAB中的wkeep1(s,len,'c')的功能
    k = (convLen - recLen)/2;
    for(i=0; i<recLen; i++)
    {
        recData[i] = convDataLow[i + k] + convDataHigh[i + k];
    }

    return recLen;
}

/**
 * @brief 小波变换之重构
 * @param cA 分解后的近似部分序列-低频部分
 * @param cD 分解后的细节部分序列-高频部分
 * @param cALength 输入数据长度
 * @param RecLength 输入重构后的原始数据长度
 * @param db 过滤器类型
 * @param recData 重构后输出的数据
 * @return 正常则返回重构数据长度，错误则返回-1
 */
int Wavelet::Reconstruction(double *cA, double *cD, int cALength, int RecLength, Filter db, double* recData)
{
    if((NULL == cA)||(NULL == cD)||(NULL == recData))
        return -1;

    m_db = db;
    int filterLen = m_db.length;

    int i,j;
    int n,k,p;
    int recLen = RecLength;

    int convLen = 0;
    double convDataLow[recLen+filterLen-1];
    double convDataHigh[recLen+filterLen-1];

    double cATemp[2*cALength];
    double cDTemp[2*cALength];

    memset(convDataLow, 0, (recLen+filterLen-1)*sizeof(double)); // 清0
    memset(convDataHigh, 0, (recLen+filterLen-1)*sizeof(double)); // 清0
    memset(cATemp, 0, 2*cALength*sizeof(double)); // 清0
    memset(cDTemp, 0, 2*cALength*sizeof(double)); // 清0

    // 1.隔点插0
    Upsampling(cA, cALength, cATemp);
    Upsampling(cD, cALength, cDTemp);

    // 2.卷积运算
    Conv1(0, cATemp, 2*cALength-1, db.lowFilterRec, filterLen ,convDataLow, &convLen);
    convLen = 0;
    Conv1(0, cDTemp, 2*cALength-1, db.highFilterRec, filterLen ,convDataHigh, &convLen);

    // 3.抽取结果及求和——实现类似MATLAB中的wkeep1(s,len,'c')的功能
    k = (convLen - recLen)/2;
    for(i=0; i<recLen; i++)
    {
    	recData[i] = convDataLow[i + k] + convDataHigh[i + k];
    }
	
    return recLen;
}

//----转自  www.cnblogs.com/IDoIUnderstand/）