拓扑排序
我们先借鉴一下别人的博客,在原本作者的博客上加上一种优化复杂度的方法。
介绍
拓扑排序,很多人都可能听说但是不了解的一种算法。或许很多人只知道它是图论的一种排序,至于干什么的不清楚。又或许很多人可能还会认为它是一种啥排序。而实质上它是对有向图的顶点排成一个线性序列。
至于定义,百科上是这么说的:
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
为什么会有拓扑排序?拓扑排序有何作用?
举个例子,学习java系列的教程
| 代号 | 科目 | 学前需掌握 |
|---|---|---|
| A1 | javaSE | |
| A2 | html | |
| A3 | Jsp | A1,A2 |
| A4 | servlet | A1 |
| A5 | ssm | A3,A4 |
| A6 | springboot | A5 |
就比如学习java系类(部分)从java基础,到jsp/servlet,到ssm,到springboot,springcloud等是个循序渐进且有依赖的过程。在jsp学习要首先掌握java基础和html基础。学习框架要掌握jsp/servlet和jdbc之类才行。那么,这个学习过程即构成一个拓扑序列。当然这个序列也不唯一,你可以对不关联的学科随意选择顺序(比如html和java可以随便先开始哪一个。)
那上述序列可以简单表示为:
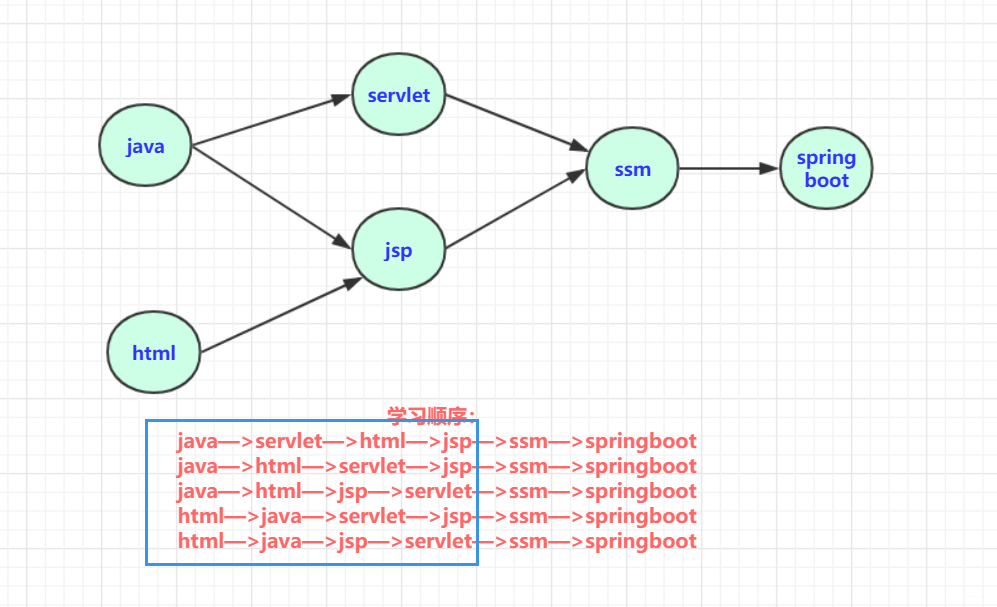
其中五种均为可以选择的学习方案,对课程安排可以有参考作用,当然,五个都是拓扑序列。只是选择的策略不同!
一些其他注意:
DGA:有向无环图
AOV网:数据在顶点 可以理解为面向对象
AOE网:数据在边上,可以理解为面向过程!
而我们通俗一点的说法,就是按照某种规则将这个图的顶点取出来,这些顶点能够表示什么或者有什么联系。
规则:
- 图中每个顶点只出现
一次。 - A在B前面,则不存在B在A前面的路径。(
不能成环!!!!) - 顶点的顺序是保证所有指向它的下个节点在被指节点前面!(例如A—>B—>C那么A一定在B前面,B一定在C前面)。所以,这个核心规则下只要满足即可,所以拓扑排序序列不一定唯一!
Conclusion:用离散数学中的语言就是,如果两个节点存在偏序关系,a<b(也可以是>,但整张图必须满足偏序关系),那么我们可以建一条由a->b的有向边。然后我们在输出排序的时候必须满足,偏序小一定在比它大的数的左边,因为偏序关系可能由多条链构成,所以排序的方法不唯一。
拓扑排序算法分析
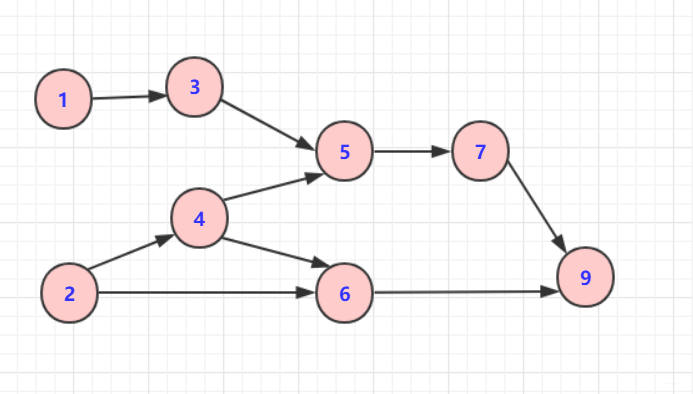
正常步骤为(方法不一定唯一):
- 从DGA图中找到一个
没有前驱的顶点输出。(可以遍历,也可以用优先队列维护) - 删除以这个点为起点的边。(它的指向的边删除,为了找到下个没有前驱的顶点)
- 重复上述,直到最后一个顶点被输出。如果还有顶点未被输出,则说明有环!
对于上图的简单序列,可以简单描述步骤为:
- 1:删除1或2输出

- 2:删除2或3以及对应边
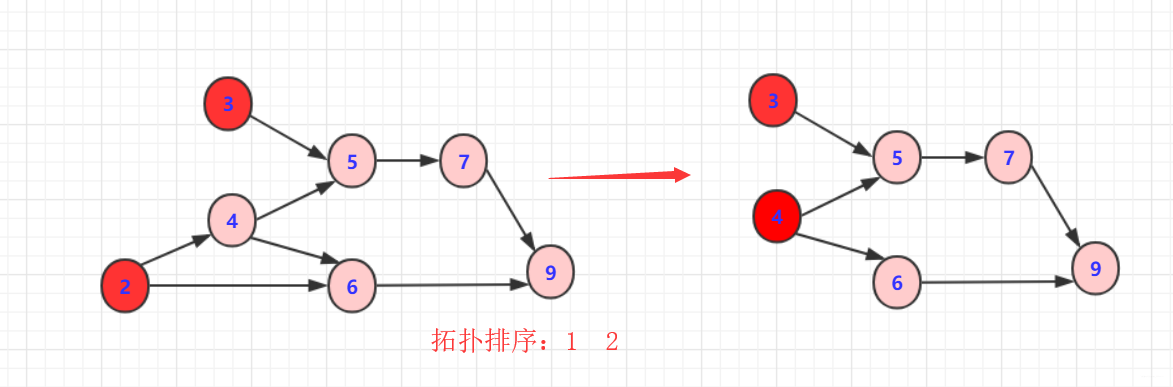
- 3:删除3或者4以及对应边
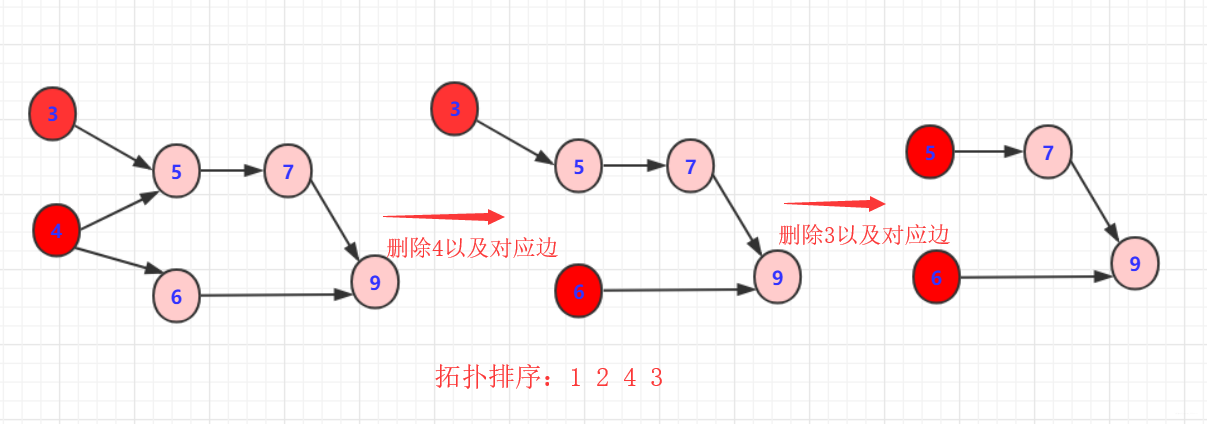
- 3:重复以上规则步骤
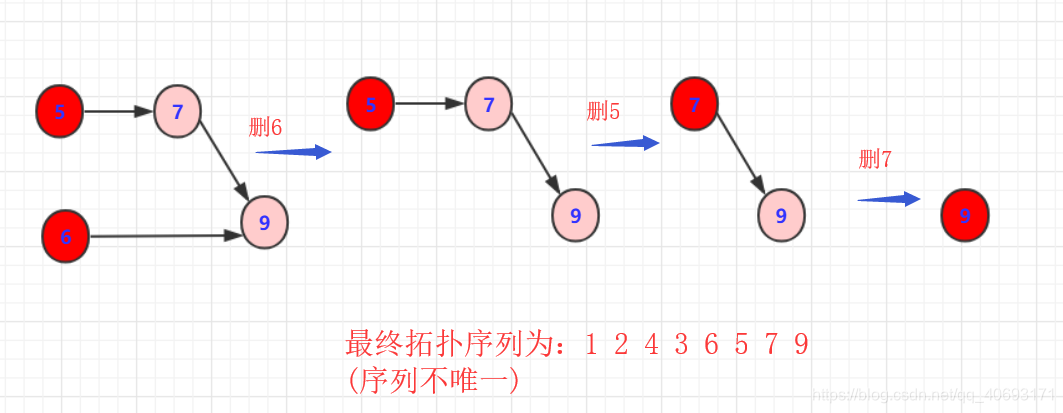
这样就完成一次拓扑排序,得到一个拓扑序列,但是这个序列并不唯一!从过程中也看到有很多选择方案,具体得到结果看你算法的设计了。但只要满足即是拓扑排序序列。
另外观察 1 2 4 3 6 5 7 9这个序列满足我们所说的有关系的节点指向的在前面,被指向的在后面。如果完全没关系那不一定前后(例如1,2)
**Conclusion: ** 我们在根据偏序关系建立边的同时,我们记入一个节点的入度,如果当前节点的入度为0,那么他肯定是个极小值(离散数学哈斯图中的概念:一条拓扑链中的最小的点),简言之他没有前继点那么他可以进入排序序列,每次进入一个以后,我们要更新每个点的入度,就是删掉与入队点有关的边。复杂度分析,确定N个点,每确定一个点要遍历一下要删掉对应的边,复杂度为O(点+边)(最优)
我们先来看基础代码段1;
#include<iostream>
#include<vector>
using namespace std;
const int N= ;//数据范围
vector<int>G[N],ans;
int b[N]={0};//记录每个点的入度
bool vis[N]={0};//每个点是否入队
int main(){
int n;
cin>>n;
for(int i=1;i<n;i++){
int f,t;
cin>>f>>t;
G[f].push_back(t);
b[t]++;
}
//拓扑排序
int i,j;
for(i=1;i<=n;i++){//需要确定n个点
for(j=1;j<=n;j++){
if(!vis[j]&&b[j]==0){
ans.push_back(j)
vis[j]=1;
break;
}
}
for(int k=0;k<G[j].size();k++) b[G[j][k]]--;
if(j==n-1){//不存在入度为0的点,存在环
cout<<"No Answer!
";
exit(0);
}
}
//输出
for(int i=0;i<ans.size();i++)
cout<<ans[i]<<" ";
return 0;
}
我们发现上面的代码中有一个地方复杂度比较高,就是每次要寻找入度为零的点要O(n)的时间,其实这个可以通过队列来优化
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
const int N= ;
int b[N]={0};
bool vis[N]={0};//用来判断第一次判断是不是入度为0
vector<int>G[N],ans;
int main(){
int n;
cin>>n;
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
vis[v]=1;
G[u].push_back(v);
b[v]++;
}
//拓扑排序
queue<int>que;
for(int i=1;i<=n;i++)
if(b[i]==0){
que.push(i);
ans.push_back(i);
}
while(!que.empty){
int t=que.top();que.pop();
for(int i=0;i<G[t].size();i++)
if(--b[G[t][i]]==0)//这个点变成入度为0
ans.push_back(G[t][i]),que.push(G[t][i]);
}
if(ans.size()==n)
for(int i=0;i<ans.size();i++)
cout<<ans[i]<<" ";
else
cout<<"No Answer!
";
}
拓扑排序其实还有一种不用dfs的做法
#include<iostream>
#include<stack>
#include<vector>
using namespace std;
const int N= ;
int vis[N]={0};//用来判断第一次判断是不是入度为0
vector<int>G[N];
stack<int>ans;
bool dfs(int x){
vis[x]=-1;//被访问过
for(int i=0;i<G[x].size();i++){
int v=G[x][i];
if(vis[v]==0)
if(dfs(v))
return 1;
else if(vis[v]==-1) return 1;
}
vis[x]=1;//注意:已经入队,我们每次在一条链上后序找需要的,无法找到他前面的点。
S.push(x);
return 0;
}
int main(){
int n;
cin>>n;
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
}
for(int i=1;i<=n;i++){
if(vis[i]==0)
if(dfs(i)){//找到环
cout<<"No Answer!
";
exit(0);
}
}
while(!S.empty()){
cout<<S.top()<<" ";
S.pop();
}
}