Amr loves Geometry. One day he came up with a very interesting problem.
Amr has a circle of radius r and center in point (x, y). He wants the circle center to be in new position (x', y').
In one step Amr can put a pin to the border of the circle in a certain point, then rotate the circle around that pin by any angle and finally remove the pin.
Help Amr to achieve his goal in minimum number of steps.
Input consists of 5 space-separated integers r, x, y, x' y' (1 ≤ r ≤ 105, - 105 ≤ x, y, x', y' ≤ 105), circle radius, coordinates of original center of the circle and coordinates of destination center of the circle respectively.
Output a single integer — minimum number of steps required to move the center of the circle to the destination point.
2 0 0 0 4
1
1 1 1 4 4
3
4 5 6 5 6
0
In the first sample test the optimal way is to put a pin at point (0, 2) and rotate the circle by 180 degrees counter-clockwise (or clockwise, no matter).
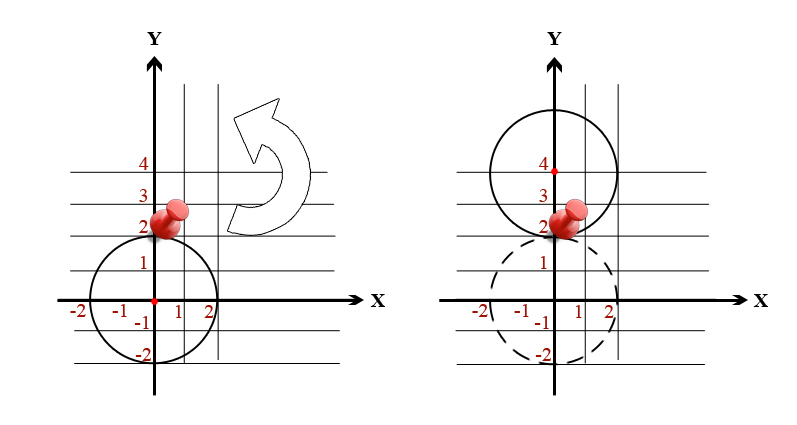
画个图可发现到以圆的边界为转动中心,可以到达的新的圆的中心集也是一个圆。
且原点x , y 到点x' , y'的关系.
是sqrt ((x-x')^2 + (y-y')^2) ..与 2*R的距离有关的。


#include<bits/stdc++.h> using namespace std; int main() { double r , x0 , y0 , x1 , y1 ; while( cin >> r >> x0 >> y0 >> x1 >> y1 ) { r *= 2.0 ; double a = fabs(x1-x0) / r , b = fabs(y1-y0) / r ; double c = sqrt( a*a + b*b ); printf("%.0lf ",ceil(c)); } }
