隆重介绍一个优秀的数据结构!!
它不像分块那样笨重——
它不像线段树那样复杂——
它拥有着logn的复杂度——
它可以快速算出逆序对数量——
树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和,但是每次只能修改一个元素的值;经过简单修改可以在log(n)的复杂度下进行范围修改,但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。
原理
首先我们要了解计算机反码与补码:
计算机界是不存在减法的——有正负号的类型int 首位存储正负号。这也就是int比unsigned int多消耗一个位数的原因。
反码相当于把所有的数字按位取反 再加1。
举个例子:
(此处把32位二进制数简写成8位)
8-5=3
写成二进制就是
0 0 0 0 1 0 0 0
+ 1 1 1 1 1 0 1 1 (5的反码)
1 0 0 0 0 0 0 1 1
首位废弃,得到(11)2=(3)10
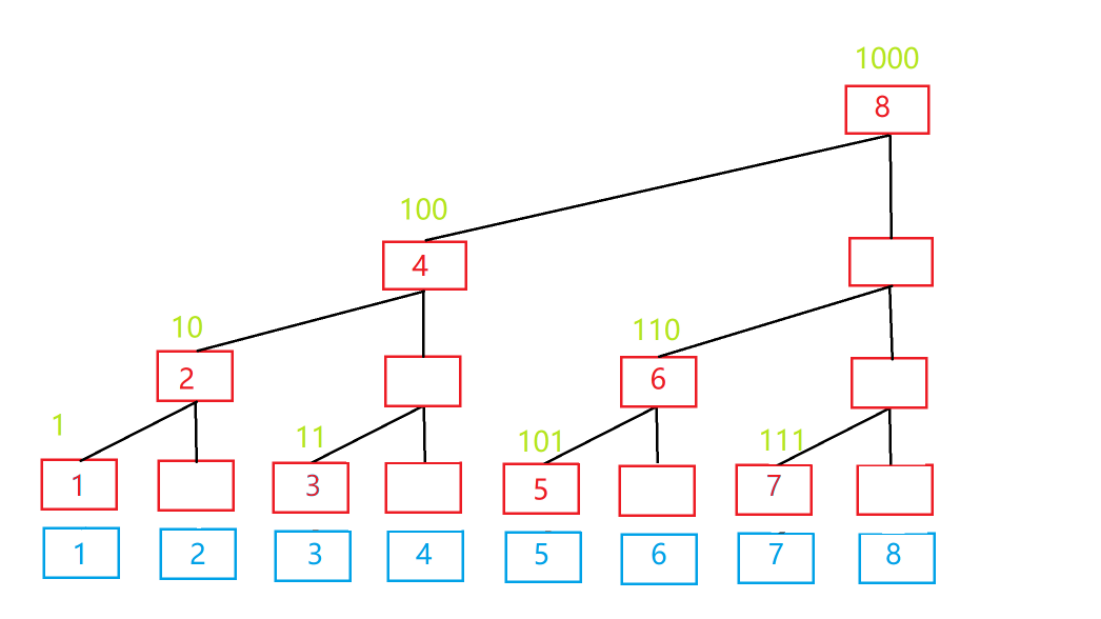
树状数组中,
s[1]=a[1]
s[2]=a[1]+a[2]
s[3]=a[3]
s[4]=a[1]+a[2]+a[3]+a[4]
转化成二进制就是:
s[1]=a[1]
s[10]=a[1]+a[10]
s[11]=a[11]
s[100]=a[1]+a[10]+a[11]+a[100]
当我们已经从下至上地建树之后,求前n项的和只需由上加到下就好了:
前一(1)项和:s[1]=s[1]
前两(10)项和:s[2]=s[10]
前三(11)项和:s[2]+s[3]=s[10]+s[11]
前四(100)项和:s[4]=s[100]
写到这里,规律已经变得非常明显了。
从下到上是i加上最低位的1所得的值,从上到下则是从减去最低为的1的值。
取出最低位的1
1 int lowbit(int x){return x & -x;}
查询
int getsum(int x){ int ans = 0; for(;x;x-=lowbit(x)) ans += s[x]; return ans; }
单点更新
1 void update(int x, int y){ 2 for(;x<=n;x+=lowbit(x)) 3 s[i] += y; 4 }