(本文是从我的旧博客迁移过来的)
问题地址:http://acm.timus.ru/problem.aspx?space=1&num=1258
前几日在博客园看到这种在线测试的时候,有一种相见恨晚的感觉,于是随便选了一道感兴趣的题(No.1258:Pool)开始做。为了准确了解题的意思,我把题翻译成中文了,这道题的原理和台球很相似(由于以前常玩可乐8,所以对台球的问题倍感亲切)。但不知道为什么出题人将台球问题说成了一个程序员撞墙的问题。下面是我翻译后的,英语不好,译错的地方请见谅。
问题:
1258. Pool
运行时间限制: 1.0 秒
内存限制: 16 MB
内存限制: 16 MB
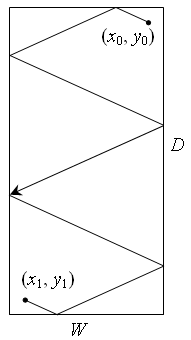
在午休的时候,程序员Vasechkin喜欢在他的矩形房间里闲逛。他从他工作的地方开始溜达,直到他有了再开始工作的念头才停止。我们已知当Vasechkin撞墙时,他的运动规律相当符合“入射角等于反射角”定律。并且Vasechkin走的路线是很直的线段。凶狠的办公室主任决定找出他浪费了多少时间在溜达上。显然Vasechkin走过的长度除以他的平均速度(事先测量)可得出所用的时间。所以必须知道这个长度!并且从Vasechkin的碰撞中能清楚的知道Vasechin的撞墙顺序。可能还有更简单的方法计算出程序员所浪费的时间,但是办公室主任认为这是解决问题的最佳方法。
输入
第一行由两个整数W和D组成——他们分别是Vasechkin所在房间的宽和长(0<=W,D<=1000,单位:米)。
第二行由Vasechkin的起始位置相对于左上角的坐标组成(0<X0<W,0<y0<D)。
第三行是终点相对于左上角的坐标(0<x1<W,0<y1<D),
最后的第四行由字母L,R,F,B组成,每个字母分别代表Vasechkin撞墙的顺序——左,右,上,下。
撞墙的次数不超过1000.
这个程序员永远不会撞在墙角,并且他的起始位置不会贴在墙上。
第二行由Vasechkin的起始位置相对于左上角的坐标组成(0<X0<W,0<y0<D)。
第三行是终点相对于左上角的坐标(0<x1<W,0<y1<D),
最后的第四行由字母L,R,F,B组成,每个字母分别代表Vasechkin撞墙的顺序——左,右,上,下。
撞墙的次数不超过1000.
这个程序员永远不会撞在墙角,并且他的起始位置不会贴在墙上。
输出
Vasechkin从起点到终点所走的长度,保留小数点后四位。
例子
| input | output |
|---|---|
10 20
9 1
1 19
FLRLRB
|
52.8015 |
出题人: Pavel Egorov
题来源: 2003年10月11日斯维尔德洛夫斯克州大学生编程公开赛
==============================================================
简单理解就是:给长宽,起点和终点,撞边的情况,最后求的是轨迹的长度。
按下图,做辅助图后,可以比较容易的根据勾股定理求出斜边。
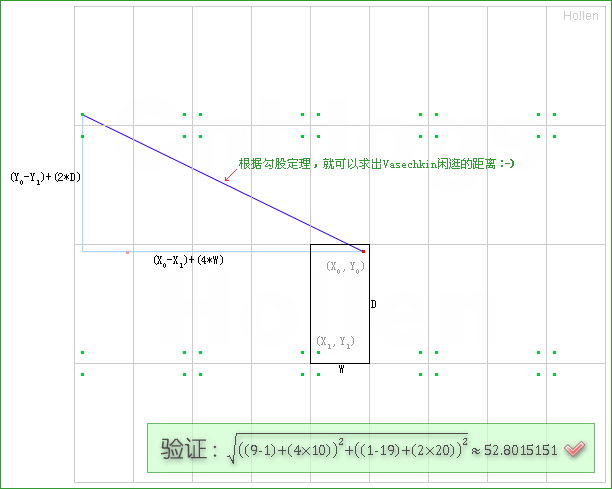
X0,X1,Y0,Y1,W,D这些都是已知的,接下来就是分析碰撞顺序与这些量的关系。
X方向的位移和Y方向的可以分别分析。
X方向的位移规律找出来了,Y方向的位移也是一样的。
不撞墙时:(X0-X1)^2和(X1-X0)^2是一样的,为了跟下面统一,所以把X0写在前面
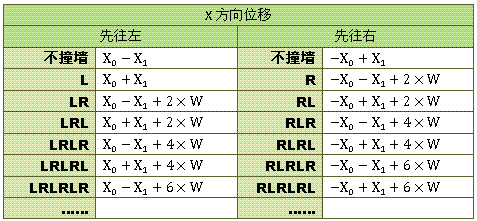
再分析一下系数的规律:
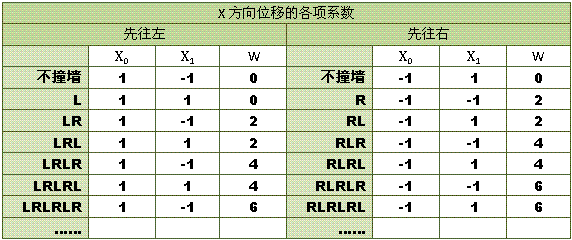
规律已经比较明显:
X0的系数规律——先往左的时候为正1,先往右的时候为负1。
X1的系数规律——碰撞次数为偶数的时候与X0系数异号,奇数时同号。
W的系数规律——R个数乘以2。
Y方向的规律也是如此。
分析到此,已经可以在程序里面方便的实现这些逻辑了。
下面是我写的代码,如果按照正确格式输入,结果是正确的。
但不知道为什么,提交到ACM系统中报错,也不知道错误是什么,调试不了,我已经是激情殆尽了。哪位朋友如果运行成功了或者发现错误了,一定要告诉我下。
有一个问题,题中要求结果保留4位小数,但我没看出来是“四舍五入”还是“直接舍去”,但我两种都试了,都说答案有误。
下面是代码:
题来源: 2003年10月11日斯维尔德洛夫斯克州大学生编程公开赛
==============================================================
简单理解就是:给长宽,起点和终点,撞边的情况,最后求的是轨迹的长度。
按下图,做辅助图后,可以比较容易的根据勾股定理求出斜边。

X0,X1,Y0,Y1,W,D这些都是已知的,接下来就是分析碰撞顺序与这些量的关系。
X方向的位移和Y方向的可以分别分析。
X方向的位移规律找出来了,Y方向的位移也是一样的。
不撞墙时:(X0-X1)^2和(X1-X0)^2是一样的,为了跟下面统一,所以把X0写在前面

再分析一下系数的规律:

规律已经比较明显:
X0的系数规律——先往左的时候为正1,先往右的时候为负1。
X1的系数规律——碰撞次数为偶数的时候与X0系数异号,奇数时同号。
W的系数规律——R个数乘以2。
Y方向的规律也是如此。
分析到此,已经可以在程序里面方便的实现这些逻辑了。
下面是我写的代码,如果按照正确格式输入,结果是正确的。
但不知道为什么,提交到ACM系统中报错,也不知道错误是什么,调试不了,我已经是激情殆尽了。哪位朋友如果运行成功了或者发现错误了,一定要告诉我下。
有一个问题,题中要求结果保留4位小数,但我没看出来是“四舍五入”还是“直接舍去”,但我两种都试了,都说答案有误。
下面是代码:
1 using System; 2 namespace ACM1258 3 { 4 class Program 5 { 6 static void Main() 7 { 8 System.Threading.Thread.CurrentThread.CurrentCulture = System.Globalization.CultureInfo.InvariantCulture; 9 10 double result; //输出 11 double sideX, sideY; //两个直角边 12 double X0,X1,Y0,Y1,W,D; //各个参数 13 string flrb; //撞墙顺序 14 int coeffX0=0,coeffX1=0,coeffY0=0,coeffY1=0,coeffW=0,coeffD=0; //各个系数 15 bool checkLorR= true,checkForB= true; //是否检查第一个LR、FB 16 bool LFirst= false,FFirst= false; //判断第一个撞哪边 17 bool FBpair= true,LRpair=true; //F与B、L与R的个数是否相等; 18 19 string[] temp; 20 temp = Console.ReadLine().Split(); //[0]:W [1]:D 21 W=Convert.ToDouble(temp[0]); 22 D=Convert.ToDouble(temp[1]); 23 temp = Console.ReadLine().Split(); //[0]:X0 [1]:Y0 24 X0=Convert.ToDouble(temp[0]); 25 Y0=Convert.ToDouble(temp[1]); 26 temp = Console.ReadLine().Split(); //[0]:X1 [1]:Y1 27 X1=Convert.ToDouble(temp[0]); 28 Y1=Convert.ToDouble(temp[1]); 29 flrb = Console.ReadLine(); 30 31 for (int i = 0; i < flrb.Length; i++) 32 { 33 switch (flrb[i]) 34 { 35 case 'F': 36 if (checkForB) 37 { 38 FFirst = true; 39 checkForB = false; 40 } 41 FBpair = !FBpair; 42 break; 43 case 'L': 44 if (checkLorR) 45 { 46 LFirst = true; 47 checkLorR = false; 48 } 49 LRpair = !LRpair; 50 break; 51 case 'R': 52 if (checkLorR) 53 { 54 LFirst = false; 55 checkLorR = false; 56 } 57 LRpair = !LRpair; 58 coeffW++; 59 break; 60 case 'B': 61 if (checkForB) 62 { 63 FFirst = false; 64 checkForB = false; 65 } 66 FBpair = !FBpair; 67 coeffD++; 68 break; 69 default: 70 break; 71 } 72 } 73 74 coeffX0 = LFirst ? 1 : -1; 75 coeffX1 = LRpair ? -coeffX0 : coeffX0; 76 coeffY0 = FFirst ? 1 : -1; 77 coeffY1 = FBpair ? -coeffY0 : coeffY0; 78 79 sideX = (coeffX0 * X0 + coeffX1 * X1) + coeffW * 2 * W; 80 sideY = (coeffY0 * Y0 + coeffY1 * Y1) + coeffD * 2 * D; 81 82 result = Math.Sqrt(sideX*sideX+sideY*sideY); 83 //result = ((int)(result * 10000)) / 10000.0; //这是直接舍去的,否则就是四舍五入 84 Console.WriteLine(result.ToString("F4")); 85 } 86 } 87 }
运行题中的测试用例结果: