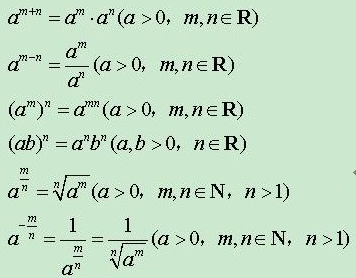预习:
先来复习一下中学的课程:
指数函数:
y=(a^x)函数(a为常数且以a>0,a≠1)叫做指数函数,函数的定义域是 R
对数函数:
如果(a^x=N)(a>0,且a≠1),那么数x叫做以a为底N的对数,记作(x=log_a^N),读作以a为底N的对数,其中a叫做对数的底数,N叫做真数。
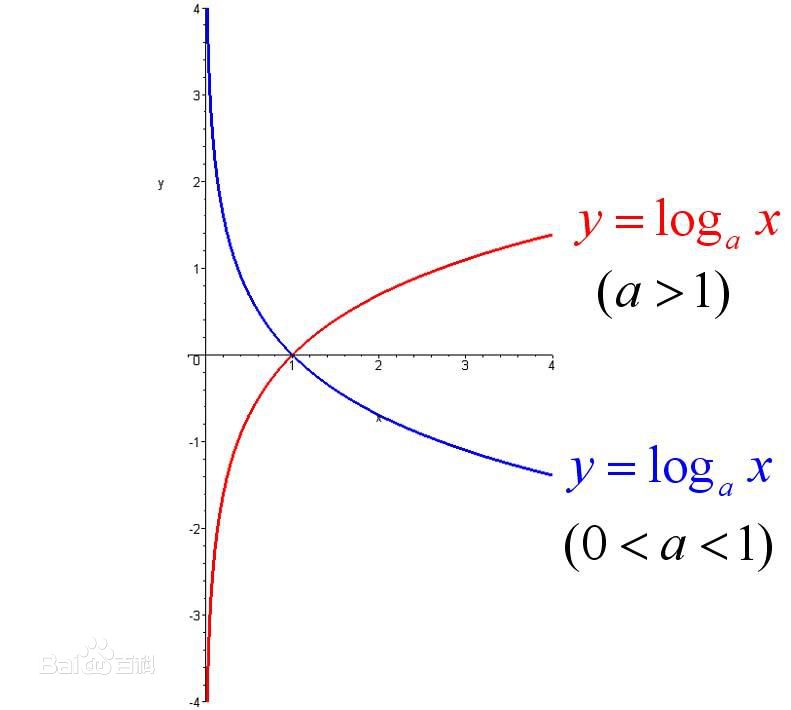
一般地,函数(y=log_a^x)(a>0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数
对数的表示及性质:
-
以a为底N的对数记作:(log_a(N))
-
以10为底的常用对数:(lg(N)) = (log_{10}(N))
-
以无理数e(e=2.71828...)为底的自然对数记作:(lnN) = (log_eN)
-
零没有对数.
-
在实数范围内,负数无对数。 [3]在虚数范围内,负数是有对数的。
自然数e
数学中的自然数e,讲解地址: http://www.ruanyifeng.com/blog/2011/07/mathematical_constant_e.html
===============================================
时间复杂度案例
先看一个log相关的时间复杂度:
int num1, num2;
for(int i=0; i<n; i++){
num1 += 1;
for(int j=1; j<=n; j*=2){
num2 += num1;
}
}
j每循环一次乘以2
j初始为1,所以循环x次以后就是(j=2^x)
(j>n)时停止循环,也就是(2^x>n),此时(x=log_2^n)
所以(j)循环了(log_2^n)次
总共计算(n*log_2^n)次