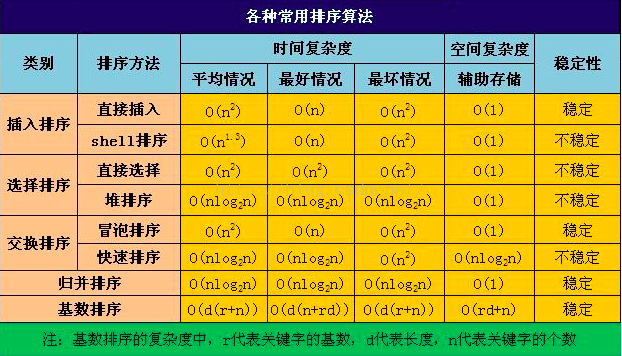
以上快速排序和归并排序的空间复杂度不正确
图2没有的参考图1,以图2为准(对,就是懒得重新画图了)
|
排序法 |
最差时间分析 | 平均时间复杂度 | 稳定度 | 空间复杂度 |
| 冒泡排序 | O(n2) | O(n2) | 稳定 | O(1) |
| 快速排序 | O(n2) | O(n*log2n) | 不稳定 | O(log2n)~O(n) |
| 选择排序 | O(n2) | O(n2) | 稳定 | O(1) |
| 二叉树排序 | O(n2) | O(n*log2n) | 不稳定 | O(n) |
|
插入排序 |
O(n2) | O(n2) | 稳定 | O(1) |
| 堆排序 | O(n*log2n) | O(n*log2n) | 不稳定 | O(1) |
| 希尔排序 | O | O | 不稳定 | O(1) |
常用排序算法
1.插入排序
由N-1趟排序组成,对于p=1到p=N-1趟,插入排序保证从位置0到位置p上的元素为已排序状态。
时间复杂度:O(N^2)
{
int j,p;
ElementType Tmp;
for(p=1;p<N;p++)
{
Tmp=A[j];//把A[j]保存下来,因为它要被插入到前面的某个位置去
for(j=p;j>0&&A[j-1]>Tmp;j--)//大于A[j]的元素逐个后移
{
A[j]=A[j-1];
}
A[j]=Tmp;
}
}
2.希尔排序
希尔排序使用一个序列h1,h2,h3,ht,叫做增量排序。在使用增量hk的一趟排序之后,对于每个i我们有A[i]<A[i+hk],所有相隔hk的元素被排序。
时间复杂度:O(N^(1+a)),其中0<a<1。
//代码不太好理解,使用了3层循环 void ShellSort(ElementType A[],int N) { int j,p,Increment; ElementType Tmp; for(Increment=N/2;Increment>0;Increment/=2) { for(p=Increment;p<N;p++) { Tmp=A[p]; for(j=p;j>=Increment;j-=Increment) { if(A[j]<A[j-Increment]) A[j]=A[j-Increment]; else break; } A[j]=Tmp; } } }
3. 堆排序
思想:建立小顶堆,然后执行N次deleteMin操作。
时间复杂度:O(NlogN),实践中,慢于sedgewick的希尔排序
空间复杂度:O(N),用于建立堆得数组
4.归并排序
使用递归把数组分为两部分分别排序,然后合并成一个数组
时间复杂度:O(NlogN)
空间复杂度:O(N)
{
int i, LeftEnd, NumELements,TmpPos;
LeftEnd=Rpos-1;
TmpPos=Lpos;
NumElements=RightEnd-Lpos+1;
while(Lpos<=LeftEnd&&Rpos<=RightEnd)
TmpArray[TmpPos++]=(A[Lpos]<A[Rpos])?A[Lpos++]:A[Rpos++];
while(Lpos<LeftEnd)
TmpArray[TmpPos++]=A[Lpos++];
while(Rpos<RightEnd)
TmpArray[TmpPos++]=A[Rpos++];
for(i=0;i<NumElements;i++,RightEnd--)
A[RightEnd]=TmpArray[RightEnd];
}
5.快速排序
对于小数组(N<20),快排不如插排好。一种好的截止范围是N=10,大于10则用快排。
快排的四步:
①如果S中元素个数是0或1,则返回
②取S中间元素v为枢纽元
③将S-{v}分成两个不相交的集合:分别是S1(小于v),和大于v的部分S2
④返回quicksort(S1),继随v,继而quicksort(S2)
时间复杂度:O(NlogN)
编程思想:1.选取枢纽元,取首尾及中间的三个元素,排序,小的排在首位,大的排在尾部,中的作为枢纽元
2.排序时把枢纽元放在Right-1的位置上,i=Left+1;j=Right-2;开始交换过程
{
int center =(Left+Right)/2;
if(A[Left]>A[Center])
swap(&A[Left],&A[Center]);
if(A[Left]>A[Right])
swap(&A[Left],&A[Right]);
if(A[Center]>A[Right])
swap(&A[Center],&A[Right]);
swap(&A[Center],&A[Right-1]);
return A[Right-1];
}
Qsort(ElementType A[],int Left,int Right)
{
int i,j;
ElementType Pivot;
if(Left+9<Right) //10个元素以上的数组使用快排
{
Pivot=Median3(A[],Left,Right);
i=Left+1;
j=Right-2;
while(A[i++]<Pivot);
while(A[j--]>Pivot);
if(i<j)
swap(&A[i],&A[j])
else
break;
swap(&A[i],&A[Right-1]);
Qsort(A,Left,i-1);
Qsort(A,i+1,Right);
}
else
InsertSort(A,Right-Left+1);
}
6.直接选择排序
描述:选出数组中最小的元素,与数组的第一个元素交换;然后选择出数组中次小的元素,与与第二个元素交换,直到完成
选择排序需要比较N(N-1)/2次,即N2次,而交换则只需要N-1次
对于是否已经排好序,或者随机文件,所花费的时间是一致的,即执行时间具有强迫性
选择排序应用在数据项比较大,键比较小的情况下,因为此时移动元素花费时间较多,而对于其他排序算法,元素移动频繁的多
{
int i, j;
int min;
for(i=0; i<N-1; i++)
{
min = i;
for(j=i+1; j<=N-1; j++)
if(A[j]<A[min]) min=j;
swap(A[i],A[min]);
}
}
空间复杂度
1、 所有的简单排序方法(包括:直接插入、起泡和简单选择)和堆排序的空间复杂度为O(1)
2、 快速排序为O(logn ),为栈所需的辅助空间;尽管快速排序只需要一个元素的辅助空间,但快速排序需要一个栈空间来实现递归。最好的情况下,即快速排序的每一趟排序都将元素序列均匀地分割成长度相近的两个子表,所需栈的最大深度为log2(n+1);但最坏的情况下,栈的最大深度为n。这样,快速排序的空间复杂度为O(log2n))
3、链式基数排序需附设队列首尾指针,则空间复杂度为O(rd )。
“哨兵”:比较次数
比如n个顺序存储元素进行排序,a[0]做“哨兵”(即a[0]不存数据,而是用作辅存空间使用)的情况
1 、直接插入排序:比较次数 最少n-1次;最多(n-1)(n+2)/2
移动次数 最少0; 最多(n-1)(n+4)/2
使用一个辅助存储空间,是稳定的排序;
2 、折半插入排序:比较次数 最少与最多同,都是n*log2n(其中2为底,下边表示同),
移动次数 最少0,最多时间复杂度为O(n2);(n的平方,以下也如此表示);
使用一个辅助存储空间,是稳定的排序;
3 、冒泡排序: 比较最少为:n-1次,最多时间复杂度表示为o(n2);
移动次数最少为0,最多时间复杂度表示为O(n2);
使用一个辅存空间,是稳定的排序;
4 、简单选择排序: 比较次数没有多少之分,均是n(n-1)/2;
移动次数最少为0,最多为3(n-1);
使用一个辅存空间,是稳定的排序;
5 、快速排序:比较和移动次数最少时间复杂度表示为O(n*log2n);
比较和移动次数最多的时间复杂度表示为O(n2);
使用的辅助存储空间最少为log2n,最多为n的平方;是不稳定的排序;
6、 堆排序: 比较和移动次数没有好坏之分,都是O(n*log2n);
使用一个辅存空间,是不稳定的排序;
7、2-路归并排序:比较和移动次数没有好坏之分,都是O(n*log2n);
需要n个辅助存储空间,是稳定的排序;
稳定性:
排序算法的稳定性是要看具体的算法实现,比如一般情况下,直接选择排序,快速排序,希尔排序,堆排序都不是稳定排序算法,基数排序,计数排序,归并排序,插入排序,冒泡排序都是稳定排序算法。
快速排序:A = {2, 2, 1},排序后A = {1,2,2}。
希尔排序:A = {1,2,5,4,4,7},排序后(k = 2);A = {1, 2, 4, 4, 5, 7} 。
堆排序:A = {2,2,1},排序后A = {1,2, 2}。
直接选择排序: A = {4, 4, 2, 5},排序后 A = {2,4, 4, 5}。
以上举例都不满足稳定性。