[Algo][July][Notes+Homework]并查集的应用

并查集顾名思义就是有“合并集合”和“查找集合”两种操作的关于数据结构的一种算法。

假设n个节点,初始时点与点之间没有连接
• 给出一系列的连接操作
• 一次连接操作不产生环,则接受,否则被抛弃 

算法课上老师出的题目太抽象了。先引入一个简单具体的问题：

reference website:

//概念描述：

https://segmentfault.com/a/1190000004023326

//例题描述

https://segmentfault.com/a/1190000000752006

假如已知有n个人和m对好友关系（存于数字r）。如果两个人是直接或间接的好友（好友的好友的好友...），则认为他们属于同一个朋友圈，请写程序求出这n个人里一共有多少个朋友圈。
假如：n = 5 ， m = 3 ， r = {{1 , 2} , {2 , 3} , {4 , 5}}，表示有5个人，1和2是好友，2和3是好友，4和5是好友，则1、2、3属于一个朋友圈，4、5属于另一个朋友圈，结果为2个朋友圈。

从这道题的角度出发，也就是有5个节点，3条边（1条边表示两个节点之间有关系）。要把互相能到达的节点合并成一个集合。最后判断父节点的个数，就是有多少个朋友圈。

1. 如何表示节点：

机构体表示法：

#define MAX 10000
struct Node
{
    int data;    //数据
    int rank;    //层级
    int father; //父节点
 }node[MAX];

数组表示法：

int father[max]; //集合index的类别
int rank[max];//集合index的层次，通常初始化为0,C++里面用rank会和某个关键字冲突，所以C++里面要换一个数组名
int data[max];//集合index的数据类型

2.初始化节点：

void init(int i){
    father[i] = i; //初始化，每个人的父节点都是自己
    rank[i] = 0; //每层都是0
}

3.合并节点：

void unionSet(int a, int b){
    a = find(a); //找a的父节点,这时候的变量a已经是自己的父节点了
    b = find(b); //找b的父节点，这时候的变量b也是自己的父节点，下面代码注意区分
    if(a == b){   //a和b的父节点相同，属于同一集合，不需要合并
        return;
    }
    if(rank[a]>rank[b]){ //a的层数比b的层数大
        father[b] = a;  //把父节点b指向a，b的父节点变成了a
    }
    else {
        father[a] = b;  //a的的父节点变成b
        if(rank[a]==rank[b]){
            rank[b]++;
        }
    } 
}

4.寻找父节点：

int find(int x){ //寻找父节点
    if(x == father[x]){  //如果这个节点是父节点则返回
        return x;
    }
    else{
        return find(father[x]);  //如果这个节点不是父节点，那么再往上寻找这个节点的father的father
    }
}

在这个过程中可以进行路径压缩：

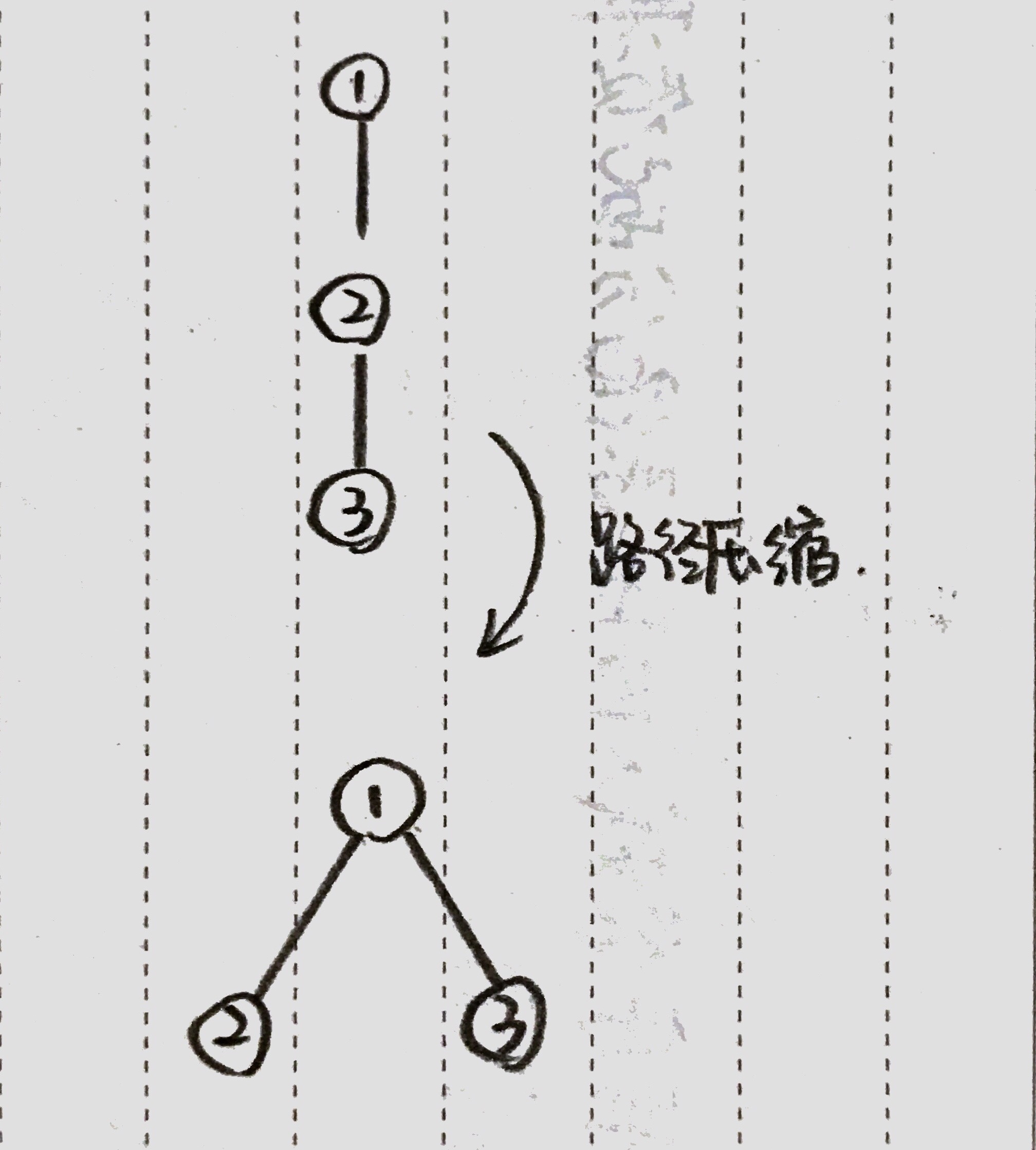
int findSet(int d){
    if(d != father[d]){
        father[d] = findSet(father[d]); //使这条路径上的所有子节点直接指向父节点
    }
    return father[d];
}

 5. 问题答案：

#include<cstdio>  
#include<iostream>
using namespace std;
#define MAX 6
int father[MAX];
int ran[MAX];
void init(){
    for(int i = 1;i < MAX;i++){
        father[i]=i;
        ran[i] = 0;
    }
}

int findSet(int d){
    if(d != father[d]){
        father[d] = findSet(father[d]);
    }
    return father[d];
}

void unionSet(int a, int b){
    a = findSet(a); 
    b = findSet(b); 

    if(a == b){   //我自己在写的时候，这其中犯了一个致命的错误，if里面的恒等条件写成了赋值，导致合并集合失败。
        return;
    }
    if(ran[a]>ran[b]){ 
        father[b] = a;  
    }
    else {
        father[a] = b;  //a的的父节点变成b
        if(ran[a]==ran[b]){
            ran[b]++;
        }
    }
}

int main()  
{  
    init();
    int m[3][2]={{1,2},{2,3},{4,5}};
    int col = sizeof(m[0])/sizeof(int); //计算列数
    int row = (sizeof(m)/sizeof(int))/col; //计算行数
    int i,j,sum = 0;
    for(i = 0; i< row; i++){
        j=0;
        while(j<col){
            unionSet(m[i][j],m[i][j++]); //输入原始关系
            j++;
        }       
    }
    for(i = 1; i<MAX; i++){
        cout<<"i:"<<i<<" father:"<<father[i];
        cout<<" rank:"<<ran[i]<<'
';
        if(findSet(i)==i) sum++; //找有几个根节点，就是有几个朋友圈
    }
    cout<<"sum: "<<sum<<endl;      
}  

输出：

Finished in 0 ms
i:1 father:1 rank:1
i:2 father:1 rank:0
i:3 father:1 rank:0
i:4 father:4 rank:1
i:5 father:4 rank:0
sum: 2

 6. 课堂作业

思路：老师也没说要做什么操作，然后又说不成环，我猜想就是如果成环的话，就没有父节点了。

int main()  
{  
    init();
    int m[5]={1,2,3,4,5};
    //cout<<col;
    int i,j,sum = 0;
    for(i = 0; i<5-1; i++){
        unionSet(m[i],m[i+1]);
    }       
    for(i = 1; i<MAX; i++){
        cout<<"i:"<<i<<" father:"<<father[i];
        cout<<" rank:"<<ran[i]<<'
';
        if(findSet(i)==i) sum++; //做了路径压缩
    }
    cout<<"sum: "<<sum<<endl;      
}  

输出：

i:1 father:2 rank:0
i:2 father:2 rank:1
i:3 father:2 rank:0
i:4 father:2 rank:0
i:5 father:2 rank:0
sum: 1

sum应该是要>0吧。。。先这样记录，等学习到后面再来更新~