BFS & 双端BFS & A* & 双边BFS
1____广度优先搜索
1.1____什么是广度优先搜索
深度优先搜索(DFS) 和 广度优先搜索(BFS)是基本的暴力技术,常用于解决图、树、的遍历,二维矩阵路径搜索,状态搜索等问题。
所谓广度优先。就是每次都尝试访问同一层的节点。 如果同一层都访问完了,再访问下一层。
这样做的结果是,BFS 算法找到的路径是从起点开始的 最短 合法路径(BFS的性质)。换言之,这条路所包含的边数最小。
在 BFS 结束时,每个节点都是通过从起点到该点的最短路径访问的。
BFS的节点访问顺序
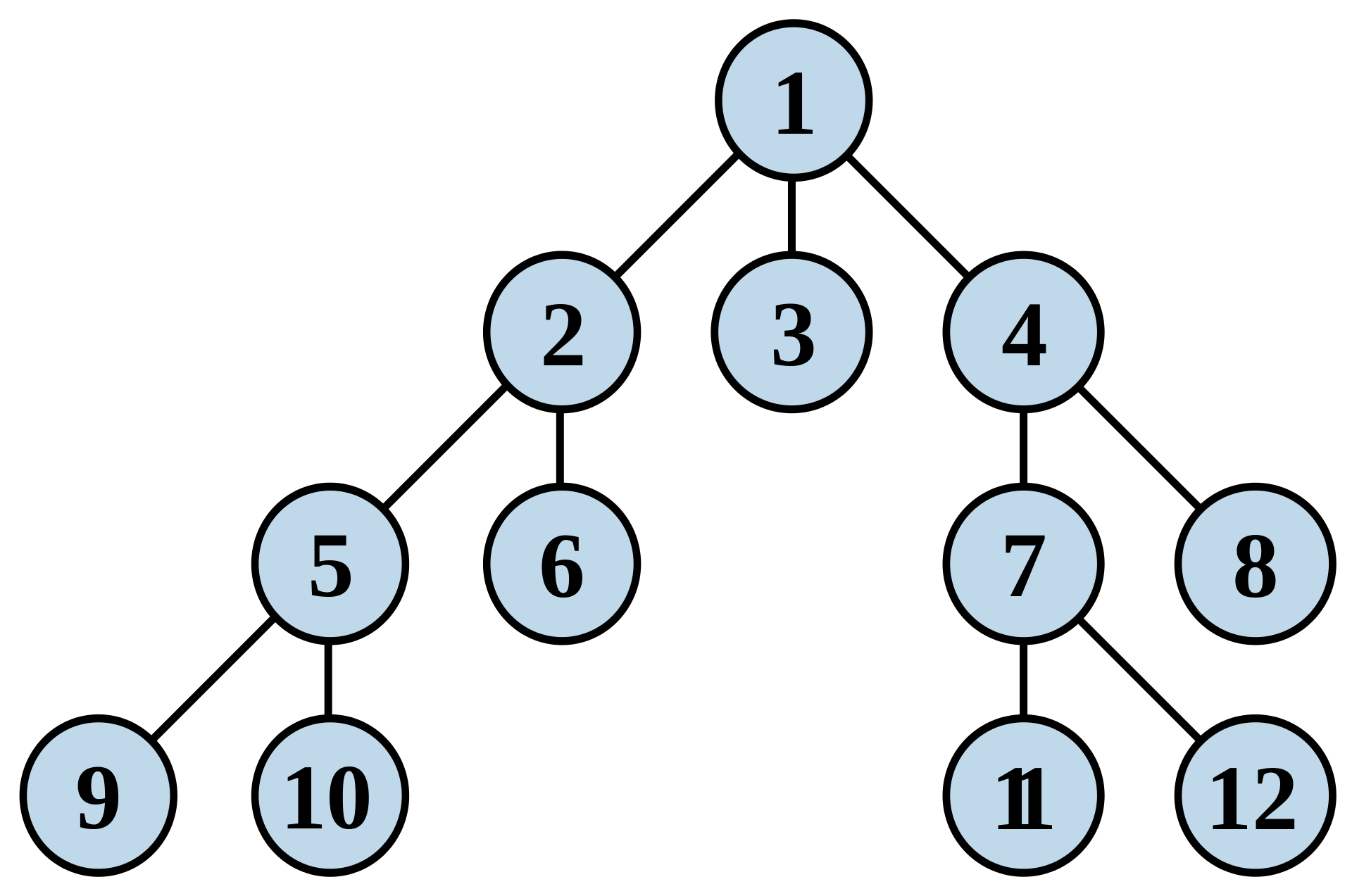
BFS是一种暴力搜索算法,目的是系统地展开并检查图(有向图,无向图,或二维图)中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能地址,彻底地搜索整张图,直到找到结果为止。BFS并不使用经验法则算法(启发式搜索)。
从算法的观点,所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。一般的实现里,其邻居节点尚未被检验过的节点会被放置在一个被称为 open 的容器中(例如队列或是链表),而被检验过的节点则被放置在被称为 closed 的容器中。(open-closed表)
1.2____深度优先与广度优先的区别
从算法思路入手,以老鼠走迷宫为例,这是DFS和BFS在现实中的模型。迷宫内部的路错综复杂,老鼠从入口进去后怎么才能找到出口?有两种方式:
-
一只老鼠走迷宫。他在每个路口都选择先走右边(也可以选择先走左边),能走多远就走多远,直到碰壁无法继续往前走,然后回退一步(或很多步直到左边有路),这一次走左边,接着继续往下走。用这个办法能走遍所有的路,而且不会重复(这里规定在回退时不算重复走)。这个思维是DFS。
-
一群老鼠走迷宫。假设老鼠是无限多的,这群老鼠进去后,在每个路口派出部分老鼠探索所有的路。走某条路的老鼠,如果碰壁无法前行,就原地停下。很显然,所有的道路都会走到,而且不会重复。这个思维就是BFS。
在具体编程的时候,一般用队列这种数据结构来具体实现BFS,甚至可以说
BFS==递归,对于DFS,也可以说DFS==递归,因为用递归实现DFS是最普遍的。DFS也可以用栈这种数据结构来直接实现,栈和递归在算法思想上是一致的
1.3____矩阵上的BFS
例1
蒜厂有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上,只能向相邻的黑色瓷砖移动。
请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
输入格式
第一行是两个整数 WW 和 HH,分别表示 xx 方向和 yy 方向瓷砖的数量。WW 和 HH 都不超过 2020。
在接下来的 HH 行中,每行包括 WW 个字符。每个字符表示一块瓷砖的颜色,规则如下
1)'.':黑色的瓷砖;
2)'#':白色的瓷砖;
3)'@':黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。输出格式
输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
Sample Input
6 9 ....#. .....# ...... ...... ...... ...... ...... #@...# .#..#.Sample Output
45
#include <bits/stdc++.h>
using namespace std;
char g[3000][3000]; /// 输入的图
bool st[3000][3000]; /// 存这个点是否被遍历过的 closed容器
int n,m; /// 矩阵大小
int dx[] = {0,0,-1,1}; /// 遍历的方向偏移量
int dy[] = {1,-1,0,0};
int ans; /// 答案
void bfs(int x1,int y1)
{
queue< pair<int,int> > q;
q.push({ x1,y1 });
st[x1][y1] = 1;
while(!q.empty()){
auto no = q.front();
q.pop();
int x = no.first , y = no.second;
//cout <<x << ' ' << y <<endl;
for(int i = 0; i < 4 ; i ++){ /// 遍历4个方向
int tx = x + dx[i];
int ty = y + dy[i];
/// 如果没有越界同时又没有被遍历过就入队列
if( g[tx][ty] == '.' && tx >= 0 && ty >= 0 && tx < n && ty < m && st[tx][ty] == 0 ){
q.push({tx,ty}); /// 入队列
st[tx][ty] = 1; /// 标记已经走过了
ans++; /// 答案+1
}
}
}
cout << ans + 1<<endl;
return ;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> m >> n;
int x,y; /// 记录'@'的位置(起点坐标)
for(int i = 0; i < n ; i++){
for(int j = 0 ; j < m ; j ++){
cin >> g[i][j];
if( g[i][j] == '@'){ ///标记起点
x = i , y = j;
}
}
}
bfs(x,y);
return 0;
}
1.4____八数码与状态图
BFS搜索处理的对象不仅可以是一个数,还可以是一种状态(划重点!)。八数码问题就是典型的状态搜索问题。
例2
在一个 3×3 的网格中,1∼8 这 8 个数字和一个
x恰好不重不漏地分布在这 3×3 的网格中。例如:
1 2 3 x 4 6 7 5 8在游戏过程中,可以把
x与其上、下、左、右四个方向之一的数字交换(如果存在)。我们的目的是通过交换,使得网格变为如下排列(称为正确排列):
1 2 3 4 5 6 7 8 x例如,示例中图形就可以通过让
x先后与右、下、右三个方向的数字交换成功得到正确排列。交换过程如下:
1 2 3 1 2 3 1 2 3 1 2 3 x 4 6 4 x 6 4 5 6 4 5 6 7 5 8 7 5 8 7 x 8 7 8 x现在,给你一个初始网格,请你求出得到正确排列至少需要进行多少次交换。
输入格式
输入占一行,将 3×3 的初始网格描绘出来。
例如,如果初始网格如下所示:
1 2 3 x 4 6 7 5 8则输入为:
1 2 3 x 4 6 7 5 8输出格式
输出占一行,包含一个整数,表示最少交换次数。
如果不存在解决方案,则输出 −1。
输入样例:
2 3 4 1 5 x 7 6 8输出样例
19
#include <bits/stdc++.h>
using namespace std;
/* 普通BFS版本 */
string en = "12345678x"; ///搜索的最终状态
unordered_map<string,int> mp; ///相当于st[]数组,用来判断是非遍历过这个状态
int dx[] = {-1,1,0,0};
int dy[] = {0,0,1,-1};
void bfs(string te)
{
/// 队列中 第一个存当前状态,第二个存到底当前状态所用的步数
queue< pair<string,int> > q;
q.push({te,0});
while( !q.empty() ){
auto no = q.front();
q.pop();
string nos = no.first;
/// 如果到达最终状态,我们就输出步数,并退出
if(nos == en){
cout << no.second <<endl;
return;
}
/// 将一维坐标,转换为二维坐标进行搜索
int loc = nos.find('x');
int x = loc / 3;
int y = loc % 3;
for(int i = 0 ; i < 4 ; i++){
int tx = x + dx[i];
int ty = y + dy[i];
if( tx >= 0 && ty >= 0 && tx < 3 && ty < 3){
swap( nos[loc] , nos[tx * 3 + ty ] );
if( mp[nos] == 0 ){
mp[nos] = 1;
q.push({nos,no.second + 1});
}
///操作完之后记得换回去,不影响下次交换
swap( nos[loc] , nos[tx * 3 + ty] );
}
}
}
cout << -1 << endl;
return ;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
string te;
for(int i = 0; i < 9 ; i++){
char tec;
cin >> tec;
te += tec;
}
bfs(te);
return 0;
}
记录路径
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <map>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
string start="";
string en = "12345678x";
map<string, pair<string,char> > path; /// 记录路径
map<string,int> mp; /// 这个状态是否枚举到了
int dx[] = {1,0,0,-1};
int dy[] = {0,-1,1,0};
char op[] = {'d','l','r','u'};
void bfs()
{
queue<string> q;
q.push(start);
mp[start] = 1;
int flag = 0;
while( !q.empty() ){
string no = q.front();
string from = no;
//cout << no << endl;
q.pop();
if( no == en ){
flag = 1;
break;
}
int loc = no.find('x');
int x = loc / 3;
int y = loc % 3;
for(int i = 0 ; i < 4 ; i++){
int tx = x + dx[i];
int ty = y + dy[i];
if( tx >= 0 && tx < 3 && ty >= 0 && ty < 3 ){
swap(no[loc] , no[tx * 3 + ty]);
if( !mp.count(no) ){
mp[no] = 1;
path[no] = make_pair(from,op[i]);
q.push(no);
}
swap(no[loc] , no[tx * 3 + ty]);
}
}
}
if( flag == 0 ){
cout << "unsolvable" <<endl;
}
else{
string ans ="";
string te = en;
while( te != start ){
ans += path[te].second;
te = path[te].first;
}
reverse( ans.begin(),ans.end() );
cout << ans <<endl;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
for(int i = 0 ; i < 9 ; i++){
char te;
cin >> te;
start += te;
}
bfs();
return 0;
}
2____ 双向广搜
所谓双向广搜,就是初始结点向目标结点和目标结点向初始结点同时扩展,直至在两个扩展方向上出现同一个结点,搜索结束。它适用的问题是,扩展结点较多,而目标结点又处在深沉,如果采用单纯的广搜解题,搜索量巨大,搜索速度慢是可想而知的,同时往往也会出现内存空间不够用的情况,这时双向广搜的作用就体现出来了。双向广搜对单纯的广搜进行了改良或改造,加入了一定的“智能因数”,使搜索能尽快接近目标结点,减少了在空间和时间上的复杂度。

可以设置两个队列,一个队列保存从起点开始搜索的状态,另一个队列用来保存从终点开始搜索的状态,当两个队列都非空时才能继续进行循环。循环内不断对元素较少的队列进行BFS操作(以免退化为单向BFS),每次操作从队列弹出一个元素,与该元素相连的后续未访问元素压入队列中。如果某一个状态出现相交的情况,那么就出现了答案。
当两种颜色相遇的时候,说明两个方向的搜索树遇到一起,这个时候就搜到了答案。
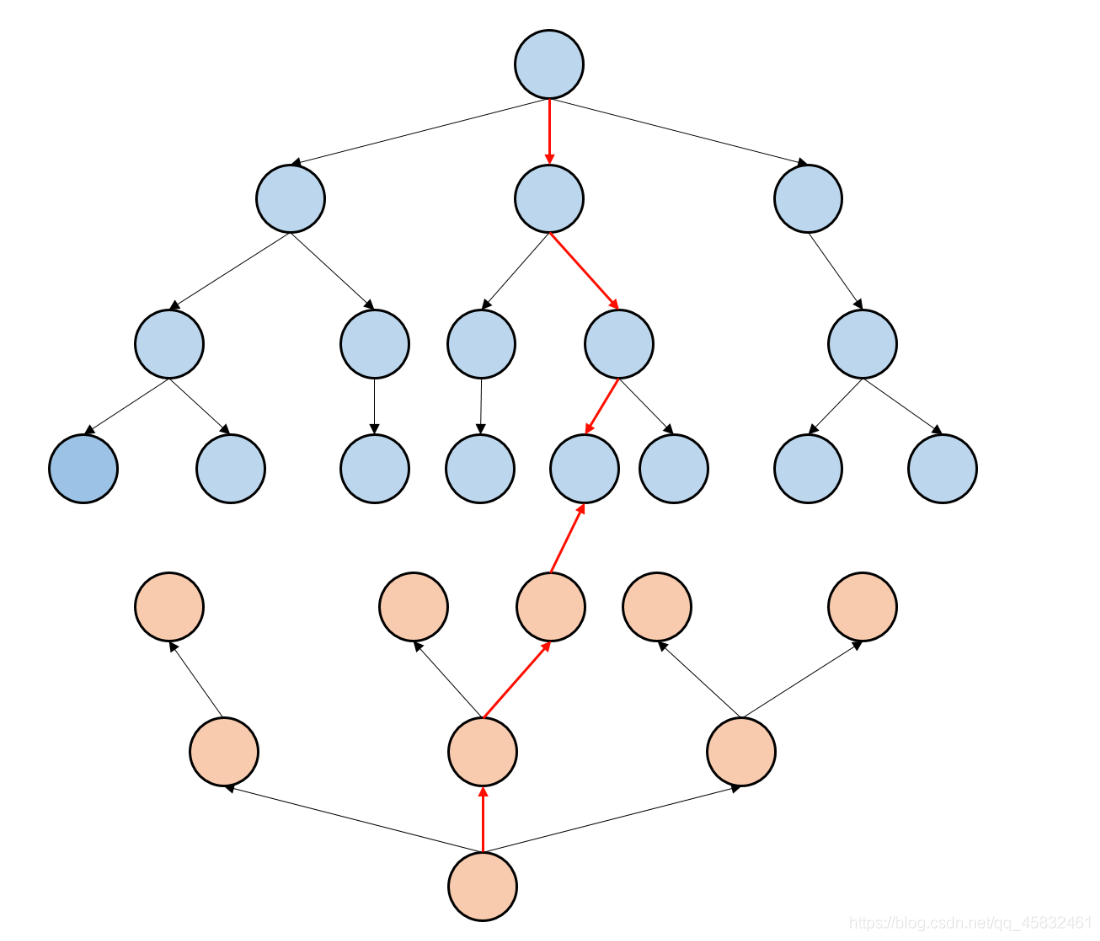
双向BFS每次不能只扩展一个点,每次要扩展一层!
已知有两个字串 A,B 及一组字串变换的规则(至多 6 个规则):
A1→B1
A2→B2
规则的含义为:在 AA 中的子串 A1A1 可以变换为 B1B1、A2A2 可以变换为 B2B2 …。
例如:A=A=
'abcd', B=B='xyz'变换规则为:
'abc' →→ 'xu'
'ud' →→ 'y'
'y' →→ 'yz'则此时,AA 可以经过一系列的变换变为 BB,其变换的过程为:
'abcd' →→ 'xud' →→ 'xy' →→ 'xyz'共进行了三次变换,使得 AA 变换为 BB。
输入格式
A B
A1 B1
A2 B2 |-> 变换规则
... ... /
所有字符串长度的上限为 20。
输出格式
若在 10 步(包含 10 步)以内能将 A 变换为 B,则输出最少的变换步数;否则输出
"NO ANSWER!"。Sample Input
abcd xyz abc xu ud y y yzSample Output
3
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <queue>
using namespace std;
const int N = 6;
int n;
string a[N], b[N];
int extend(queue<string>& q, unordered_map<string, int>& da, unordered_map<string, int>& db, string a[], string b[])
{
for (int k = 0, sk = q.size(); k < sk; k ++ )
{
string t = q.front();
q.pop();
for (int i = 0; i < t.size(); i ++ )
for (int j = 0; j < n; j ++ )
if (t.substr(i, a[j].size()) == a[j])
{
string state = t.substr(0, i) + b[j] + t.substr(i + a[j].size());
if (da.count(state)) continue;
if (db.count(state)) return da[t] + 1 + db[state];
da[state] = da[t] + 1;
q.push(state);
}
}
return 11;
}
int bfs(string A, string B)
{
queue<string> qa, qb;
unordered_map<string, int> da, db;
qa.push(A), da[A] = 0;
qb.push(B), db[B] = 0;
while (qa.size() && qb.size())
{
int t;
if (qa.size() <= qb.size()) t = extend(qa, da, db, a, b);
else t= extend(qb, db, da, b, a);
if (t <= 10) return t;
}
return 11;
}
int main()
{
string A, B;
cin >> A >> B;
while (cin >> a[n] >> b[n]) n ++ ;
int step = bfs(A, B);
if (step > 10) puts("NO ANSWER!");
else printf("%d
", step);
return 0;
}
3____ A* 算法在BFS上的应用
和八数码一样的题,但是要输出路径
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <map>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
string sta,seq;
string en = "12345678x";
map<string,int> dist; ///判重
map<string,pair<string,char> > cost; ///路径记录
priority_queue<pair<int,string> ,vector<pair<int,string> >,greater<pair<int,string> > > q; ///将启发函数数值小的排前面
int dx[] = {1,0,0,-1};
int dy[] = {0,-1,1,0};
char op[] = {'d','l','r','u'};
int get(string s) ///启发函数
{
int res = 0;
for(int i = 0 ; i < 9 ; i++)
{
if(s[i] != 'x')
{
int t = s[i] - '1';
res += abs(t / 3 - i / 3) + abs(t % 3 - i % 3);
}
}
return res;
}
void bfs(string s)
{
q.push( make_pair(get(s),s) );
dist[s] = 1;
while(!q.empty()){
pair<int,string> no = q.top();
q.pop();
string from = no.second;
string state = from;
if( no.second == en ){
break;
}
//cout << no.first << endl;
int loc = state.find('x');
int k = dist[state];
int x = loc / 3;
int y = loc % 3;
for(int i = 0 ; i < 4; i++){
int tx = x + dx[i] , ty = y + dy[i];
if(tx < 3 && ty < 3 && tx >=0 && ty >=0){
swap( state[loc],state[tx*3 + ty] );
if( dist[state] == 0 || dist[state] > k + 1 ){
dist[state] = k+1;
q.push(make_pair(dist[from]+get(state),state) );
cost[state] = make_pair(from,op[i]);
}
swap( state[loc],state[tx*3 + ty] );
}
}
}
if( dist[en] == 0){
cout << "unsolvable" <<endl;
}else{
string res="";
string te = en;
while( te != sta ){
res +=cost[te].second;
te = cost[te].first;
}
reverse(res.begin(),res.end());
cout <<res <<endl;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
for(int i =0 ; i < 9 ; i++){
char c;
cin >> c;
sta+=c;
if(c != 'x') seq += c;
}
int cnt = 0;
for(int i = 0 ; i < 8 ; i ++)
for(int j = i + 1 ; j < 8 ; j++)
if(seq[i] > seq[j])
cnt++;
if(cnt % 2) puts("unsolvable");
else bfs(sta);
return 0;
}
4____双端BFS( 双端队列在BFS上的应用 )
双端队列 BFS 又称 0-1 BFS
适用范围
边权值为可能有,也可能没有(由于 BFS 适用于权值为 1 的图,所以一般是 0 or 1),或者能够转化为这种边权值的最短路问题。
例如在走迷宫问题中,你可以花 1 个金币走 5 步,也可以不花金币走 1 步,这就可以用 0-1 BFS 解决。
实现
一般情况下,我们把没有权值的边扩展到的点放到队首,有权值的边扩展到的点放到队尾。这样即可保证在整个队列中,像普通 BFS 一样,越靠近队首,权值越小,且权值零一之间有分隔。
伪代码
while (队列不为空) {
int u = 队首;
弹出队首;
for (枚举 u 的邻居) {
更新数据
if (...)
添加到队首;
else
添加到队尾;
}
}
例
"The Chamber of Secrets has been opened again" — this news has spread all around Hogwarts and some of the students have been petrified due to seeing the basilisk. Dumbledore got fired and now Harry is trying to enter the Chamber of Secrets. These aren't good news for Lord Voldemort. The problem is, he doesn't want anybody to be able to enter the chamber. The Dark Lord is going to be busy sucking life out of Ginny.
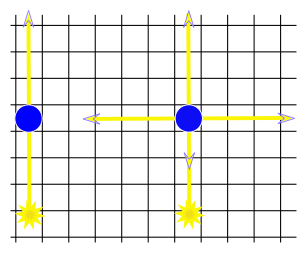
The Chamber of Secrets is an n × m rectangular grid in which some of the cells are columns. A light ray (and a basilisk's gaze) passes through the columns without changing its direction. But with some spell we can make a column magic to reflect the light ray (or the gaze) in all four directions when it receives the ray. This is shown in the figure below.
The left light ray passes through a regular column, and the right ray — through the magic column.
The basilisk is located at the right side of the lower right cell of the grid and is looking to the left (in the direction of the lower left cell). According to the legend, anyone who meets a basilisk's gaze directly dies immediately. But if someone meets a basilisk's gaze through a column, this person will get petrified. We know that the door to the Chamber is located on the left side of the upper left corner of the grid and anyone who wants to enter will look in the direction of its movement (in the direction of the upper right cell) from that position.
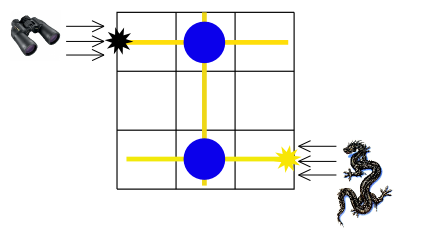
This figure illustrates the first sample test.
Given the dimensions of the chamber and the location of regular columns, Lord Voldemort has asked you to find the minimum number of columns that we need to make magic so that anyone who wants to enter the chamber would be petrified or just declare that it's impossible to secure the chamber.
Input
The first line of the input contains two integer numbers n and m (2 ≤ n, m ≤ 1000). Each of the next n lines contains m characters. Each character is either "." or "#" and represents one cell of the Chamber grid. It's "." if the corresponding cell is empty and "#" if it's a regular column.
Output
Print the minimum number of columns to make magic or -1 if it's impossible to do.
Examples
input
3 3 .#. ... .#.output
2input
4 3 ##. ... .#. .#.output
2Note
The figure above shows the first sample test. In the first sample we should make both columns magic. The dragon figure represents the basilisk and the binoculars represent the person who will enter the Chamber of secrets. The black star shows the place where the person will be petrified. Yellow lines represent basilisk gaze moving through columns.
题意:
一个 (n * m) 的图,现在有一束激光从左上角往右边射出,每遇到 '#',你可以选择光线往四个方向射出,或者什么都不做,问最少需要多少个 '#' 往四个方向射出才能使光线在第 (n) 行往右边射出。
#include <bits/stdc++.h>
#define nox no.x+dx[no.dis]
#define noy no.y+dy[no.dis]
using namespace std;
const int INF = 0x3f3f3f3f;
char g[1001][1001]; /// 输入图
int st[1001][1001][4]; /// 是否到达过
int dx[] = {0,1,0,-1}; /// 右,下,左,上
int dy[] = {1,0,-1,0};
struct node /// BFS中队列的结构体
{
int x,y; /// 坐标
int dis; /// 移动的方向
/// 0 = 右 , 1 = 下, 2 = 左,4 = 上
};
int n , m;
void bfs()
{
deque<node> q;
st[0][0][0] = 0;
q.push_front({0,0,0});
while( !q.empty() ){
auto no = q.front();
q.pop_front();
/// 正常的找到答案
if( no.x == n-1 && no.y == m-1 && no.dis == 0 ){
break;
}
/// 判一下特殊情况
if( g[n-1][m-1] == '#' && no.x == n-1 && no.y == m-1 ){
st[no.x][no.y][0] = st[no.x][no.y][no.dis] + 1;
break;
}
/// 把不操作的放在队首
if( st[nox][noy][no.dis] == INF && nox >= 0 && noy >= 0 && nox < n && noy < m ){
q.push_front({ nox,noy,no.dis});
st[nox][noy][no.dis] = st[no.x][no.y][no.dis];
}
if( g[ no.x ][ no.y ] == '#' ){
/// 把操作的放在队尾
for(int i = 0; i < 4 ; i++){
int tx = no.x + dx[i];
int ty = no.y + dy[i];
if( st[tx][ty][i] == INF && tx >= 0 && ty >= 0 && tx < n && ty < m ){
st[tx][ty][i] = st[no.x][no.y][no.dis] + 1;
q.push_back({tx,ty,i});
}
}
}
}
if( st[n-1][m-1][0] != INF ){
cout << st[n-1][m-1][0] <<endl;
}else{
cout << -1 <<endl;
}
return ;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
cin >> g[i][j];
}
}
for(int i = 0 ; i < n ; i++){
for(int j = 0; j < m ; j++){
st[i][j][0] = st[i][j][3] = st[i][j][2] = st[i][j][1] = INF;
}
}
bfs();
return 0;
}
5____习题
字串变换 - 计蒜客 T2159_双向广搜
Eight - POJ 1077_A*
Chamber of Secrets_Codeforces_双端BFS
Find a way - HDU 2612_BFS)
#include <bits/stdc++.h>
using namespace std;
int INF = 0x3f3f3f3f;
int n,m;
int st1[210][210];
int st2[210][210];
char g[210][210];
int dx[] = {0,0,-1,1};
int dy[] = {1,-1,0,0};
void bfs(int x, int y ,int st[][210])
{
queue< pair<int,int> > q;
q.push({x,y});
st[x][y] = 0;
while( !q.empty() ){
auto no = q.front();
q.pop();
int xx = no.first;
int yy = no.second;
for(int i = 0 ; i < 4 ; i++){
int tx = xx+ dx[i];
int ty = yy + dy[i];
if( tx >= 0 && ty >= 0 && tx < n && ty <m && st[tx][ty] == 0 && g[tx][ty] != '#' ){
st[tx][ty] = st[xx][yy] +1;
q.push({tx,ty});
}
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
while(cin >> n >> m){
int x1,x2,y1,y2;
vector< pair<int,int> > vec;
memset(st1,0,sizeof st1);
memset(st2,0,sizeof st2);
memset(g,0,sizeof g);
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < m ; j ++){
cin >> g[i][j];
if( g[i][j] == 'Y' ){
x1 =i , y1 = j;
}
if( g[i][j] == 'M' ){
x2 = i ,y2 = j;
}
if( g[i][j] == '@' ){
vec.push_back({i,j});
}
}
}
bfs(x1,y1,st1);
bfs(x2,y2,st2);
int len = vec.size();
int ans = 0x3f3f3f3f;
for(int i = 0 ; i < len ; i++){
int x = vec[i].first , y = vec[i].second;
if( st1[x][y] + st2[x][y] < ans && st1[x][y] + st2[x][y] != 0){
ans= st1[x][y] + st2[x][y];
}
}
cout << ans* 11 <<endl;
}
return 0;
}