贪心 & 栈 & 队列 & 优先队列
1____贪心:选择当前最优解
1.1____什么是贪心
贪心算法(Greedy Algorithm),是用计算机来模拟一个“贪心”的人做出决策的过程。这个人十分贪婪,每一步行动总是按某种指标选取最优的操作。而且他目光短浅,总是只看眼前,并不考虑以后可能造成的影响。
具体思路是把整个问题,分解成多个步骤,在每个步骤都选取当前步骤的最优方案,直到所有步骤结束;在每一步都不用考虑后续步骤的影响,在后续步骤中也不再回头改变前面的选择。

需要注意的是,如果题目无法证明局部最优解能得到全局最优解,那么这个题大概率上使用贪心算法是不适合的。
贪心算法在有最优子结构的问题中尤为有效。最优子结构的意思是问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。
我们后面将会学到的很多算法都有着贪心的思想:
- 最小生成树
- 单源最短路 Dijkstra 算法
- ...
1.2____局部最优解
由于运用贪心策略解题在每一次都取得了最优解,但能够保证局部最优解得不一定是贪心算法。如大家所熟悉得动态规划算法就可以满足局部最优解,在广度优先搜索(BFS)中的解题过程亦可以满足局部最优解。
在遇到具体问题时,往往分不清哪些题该用贪心策略求解,哪些题该用动态规划法求解。在此,我们对两种解题策略进行比较。
例1


例2:Chocolate Buying

1.3____贪心与动态规划
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能,也就是说之前的计算结果(子问题1),会影响后续的计算结果(子问题k)。
2____栈和队列,优先队列
2.1____FILO 栈
首先,我们来设想这样一个场景,如果厨房里有一些散乱的盘子,我们试图把它们整理在一起。于是我们把其中一个摆放在某个平稳的位置上,假设标记这第一个盘子为 (P_0) 。然后我们继续把 (p_1) 放在它的上面,之后是 (P_2) ... 直到原来散乱的盘子中最后一个 (P_n) 被摞放到了这堆盘子的最上方。

那么我们再思考个问题,如果我们想用这堆盘子,是如何取他的。显然从中间,或者从底部取盘子不是一个明智的决定,因为那样很容易将这堆盘子摔碎。最合理的方法就是从最上面开始取。
这个例子是现实生活中一个模拟栈结构的典型例子。
栈是计算机科学中一种重要的数据结构,它有很多不同的应用。从比较简单的应用到复杂的应用,随处可见,栈的影子,例如字符串反转,函数活动记录的维护等。
栈的性质
-
对于元素的访问有限制,只能访问栈顶的元素
-
在栈中元素的添加和删除都只在顶部进行
-
栈中原始的添加和删除遵守 先进后出原则(First In List Out —— FILO)
-
如果想访问元素,只有当他在栈顶的时候才能访问(有别于数组的随机存取)


操作代码
| 操作 | 代码 |
|---|---|
| 入栈 | sta.push(x) |
| 出栈(只能出栈顶) | sta.pop() |
| 取元素(只能取栈顶) | sta.top() |
| 判空 | sta.empty() 返回bool值 |
| 取栈大小 | sta.size() |
#include <stack> //头文件
//stack< 数据类型 > 栈名
stack<int> sta;
int main()
{
//入栈
sta.push(1);
//取元素,只能取栈顶元素
sta.top();
//出栈,只能出栈顶元素
sta.pop();
//判空
if( sta.empty() ){
cout << "栈为空" <<endl;
}
//取栈大小
cout << sta.size() << endl;
//清空栈
sta.clear();
}
例3

2.2____FIFO 队列
队列在实际生活中的应用就更多了。例如在电影院的售票口排队等待买票的人,就是通过队列这种数据结构组织在一起的。人们按照先来后到的顺序排成一队,最先买到票的人就是最先来的人。当某人买完票后,他就从队列的最前端离开,这就相当于删除操作,而添加的操作仅能在队列的尾部进行。
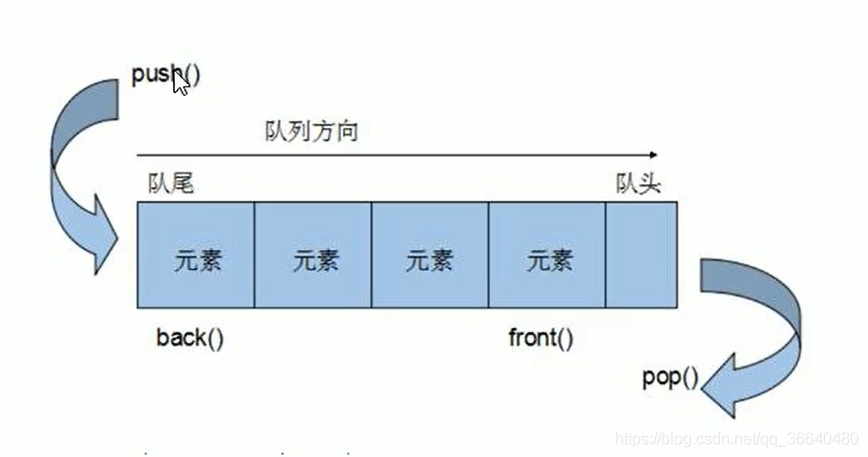
队列的性质
- 对于元素的访问有限制,只能访问队首,队尾的元素
- 在队列中元素的添加只能在队尾进行,删除只能在队首进行。
- 队列中原始的添加和删除遵守 先进先出原则(First In First Out —— FIFO)
- 如果想访问元素,只能访问队首 和 队尾 元素
操作代码
| 操作 | 代码 |
|---|---|
| 入队(只能入队尾) | que.push(x) |
| 出队(只能出队首) | que.pop() |
| 取队首 | que.front() |
| 取队尾 | que.back() |
| 判空 | que.empty() 返回bool值 |
| 取队列大小 | que.size() |
#include <queue> //头文件
//queue< 数据类型 > 队列名
queue<int> queue;
int main()
{
//入队
que.push(1);
//取队首
que.front();
//取队尾
que.front();
//出队
que.pop();
//判空
if( que.empty() ){
cout << "队列为空" <<endl;
}
//取队列大小
cout << que.size() << endl;
//清空队列
que.clear();
}
2.3____优先队列:优先级高的元素始终在队首
我们继续来看一个场景,假设某个公司仅有一台可以工作的打印机,且这台打印机既要打印员工的文件,又要打印经理的文件。如果经理的文件来的比普通员工晚,那么经理就要等待了,而通常经理的文件一般都总是比普通员工的文件更加总要。显然此时先来后到的原则用在这里就不合适了。
我们通常把打印机中的待打印任务组织在具有优先级排序的队列中的方式来解决这个问题。打印机每次根据一定的优先级次序从队列任务中取出文件(依然是每次都取队首)或者说是每次从队尾插入一个新的打印任务时,根据优先级重新对队列元素排序。
这样一来,及时经理的文件来得比较晚,如果他有足够高的优先级,那么打印机就会优先处理这个文件。如果若干的任务的优先级相同,那么打印机将安装先来先服务的顺序完成它们。
优先队列首先为队列,其次才为优先队列,也就是说,优先队列满足队列的所有性质,先进先出,限制性存取...,在满足这些性质的基础之上,增加一个基于优先级的重排序,这就是优先队列。
操作代码
| 操作 | 代码 |
|---|---|
| 入队(只能入队尾) | pro.push(x) |
| 出队(只能出队首) | que.pop() |
| 取队首 | que.top() |
| 判空 | que.empty() 返回bool值 |
| 取队列大小 | que.size() |
需要注意的是优先队列只能取队首,不能取队尾
#include <queue> //头文件
//基础写法 :priority_queue< 数据类型 > 队列名
priority_queue<int> queue;
int main()
{
//入队
pro.push(1);
//取队首
pro.top();
//出队
pro.pop();
//判空
if( pro.empty() ){
cout << "队列为空" <<endl;
}
//取队列大小
cout << pro.size() << endl;
//清空队列
pro.clear();
}
例4: fence repair

2.4____优先队列的实现——堆数据结构
堆是一棵完全二叉树,其每个节点都有一个键值,且每个节点的键值都大于等于/小于等于其父亲的键值。
每个节点的键值都大于等于其父亲键值的堆叫做小根堆,每个节点的键值都小于等于其父亲键值的堆叫做叫做大根堆。priority_queue其实就是一个大根堆。
在大根堆中,左儿子是大于右儿子的
在小根堆中,右儿子是大于左儿子的

如何实现堆的数据结构请写在自己的板子中(周日晚上交)
2.5____优先队列优先级设置
priority_queue<int,vector<int>,less<int> > //注意最后两个'>'之间必须有空格,不然会被识别为输出重定向符号'>>'
首先<>内的第一个int 和上面的代码是一样的,第二个参数vector<int>是来承载底层数据结构堆heap的容器,如果第一个参数是double型,则此处只需填写vector<double> 或vector<char>;而第三个参数 less<int> 则是对一个参数的比较类,less<int> 表示数字越大优先级越大,而greater<int> 表示数字小的优先级大。
对于自定义Struct数据,优先级设置
下去思考如何实现,明天讲