前缀和 & 差分 & 位运算 & Hash函数
1____前缀和
前缀和是一种重要的预处理,能大大降低查询的时间复杂度。可以简单理解为数列的前 n 项的和。
例1
给定一个长度为 n 的数列,请你求出数列中每个数的二进制表示中 1 的个数。
输入格式
第一行包含整数 n。
第二行包含 n 个整数,表示整个数列。
输出格式
共一行,包含 n 个整数,其中的第 i 个数表示数列中的第 i 个数的二进制表示中 1 的个数。
数据范围
1≤n≤100000,
0≤数列中元素的值≤ (10^9)数列中元素的值≤(10^9)输入样例:
5 1 2 3 4 5输出样例:
1 1 2 1 2
#include <bits/stdc++.h>
using namespace std;
int const maxn = 1e5 + 5;
int a[maxn] , dp[maxn], an[maxn];
void solve(){
int n, k;
cin >> n >> k;
for(int i = 1; i <= n; ++i) cin >> a[i];
long long ans = 0;
dp[0] = 1;
for(int i = 1; i <= n; ++i){
int te = (a[i] + an[i - 1]) % k;
ans += dp[te];
dp[te]++;
an[i] = (an[i - 1] + a[i]) % k;
}
cout << ans << endl;
}
int main (){
solve();
}
例2
最大数
N个数围成一圈,要求从中选择若干个连续的数(注意每个数最多只能选一次)加起来,问能形成的最大的和。
输入描述:
第一行输入N,表示数字的个数,第二行输入这N个数字。
输出描述:
输出最大和。
样例输入:
8 2 -4 6 -1 -4 8 -1 3样例输出:
14数据范围及提示:
40% 1<=N<=300
60% 1<=N<=2000
100% 1<= N<=100000,答案在longint范围内。
2____差分

例3
某校大门外长度为L的马路上有一排树,每两棵相邻的树之间的间隔都是1米。我们可以把马路看成一个数轴,马路的一端在数轴0的位置,另一端在L的位置;数轴上的每个整数点,即0,1,2,……,L,都种有一棵树。
马路上有一些区域要用来建地铁,这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数,区域之间可能有重合的部分。现在要把这些区域中的树(包括区域端点处的两棵树)移走。你的任务是计算将这些树都移走后,马路上还有多少棵树。Input
输入的第一行有两个整数L(1 <= L <= 10000)和 M(1 <= M <= 100),L代表马路的长度,M代表区域的数目,L和M之间用一个空格隔开。接下来的M行每行包含两个不同的整数,用一个空格隔开,表示一个区域的起始点和终止点的坐标。
Output
输出包括一行,这一行只包含一个整数,表示马路上剩余的树的数目。
Sample Input
500 3 150 300 100 200 470 471Sample Output
298
3____位运算
位运算就是基于整数的二进制表示进行的运算。由于计算机内部就是以二进制来存储数据,位运算是相当快的。
基本的位运算共6种,分别为按位与、按位或、按位异或、按位取反、左移和右移。
为了方便叙述,下文中省略“按位”。
3.1____与、或、异或
这三者都是两数间的运算,因此在这里一起讲解。
它们都是将两个整数作为二进制数,对二进制表示中的每一位逐一运算。
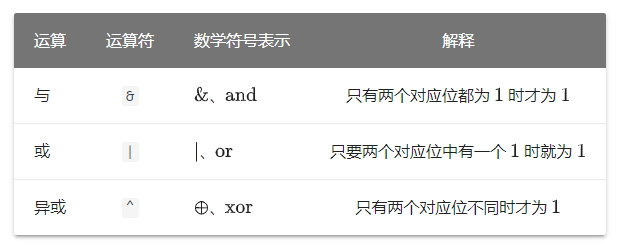
注意区分逻辑与(对应的数学符号为 $wedge $ )和按位与、逻辑或( $vee $)和按位或的区别。网络中的资料中使用的符号多有不规范之处,以上下文为准。
异或运算的逆运算是它本身,也就是说两次异或同一个数最后结果不变,即 (a oplus b oplus b = a) 。
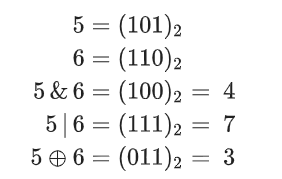
3.2____取反
取反是对一个数 (num) 进行的位运算,即单目运算。
取反暂无默认的数学符号表示,其对应的运算符为 ~。它的作用是把 的二进制补码中的 (0) 和 (1) 全部取反( (0) 变为 (1),(1) 变为 (0))。有符号整数的符号位在 ~ 运算中同样会取反。
补码:在二进制表示下,正数和 (0) 的补码为其本身,负数的补码是将其对应正数按位取反后加一。

3.3____左移和右移
num << i 表示将 (num) 的二进制表示向左移动 (i) 位所得的值。
num >> i 表示将 (num) 的二进制表示向右移动 (i) 位所得的值。

3.4____复合赋值位运算符
和 += , -= 等运算符类似,位运算也有复合赋值运算符: &= , |= , ^= , <<= , >>= 。(取反是单目运算,所以没有。)
3.5____位运算的应用
位运算一般有三种作用:
- 高效地进行某些运算,代替其它低效的方式。
- 表示集合。(常用于 状压 DP 。)
- 题目本来就要求进行位运算。
需要注意的是,用位运算代替其它运算方式(即第一种应用)在很多时候并不能带来太大的优化,反而会使代码变得复杂,使用时需要斟酌。(但像“乘 2 的非负整数次幂”和“除以 2 的非负整数次幂”就最好使用位运算,因为此时使用位运算可以优化复杂度。)
3.6____操作一个数的二进制位
- 获取一个数二进制的某一位:
// 获取 a 的第 b 位,最低位编号为 0
int getBit(int a, int b) { return (a >> b) & 1; }
- 将一个数二进制的某一位设置为0:
// 将 a 的第 b 位设置为 0 ,最低位编号为 0
int unsetBit(int a, int b) { return a & ~(1 << b); }
- 将一个数二进制的某一位设置为1:
// 将 a 的第 b 位设置为 1 ,最低位编号为 0
int setBit(int a, int b) { return a | (1 << b); }
- 将一个数二进制的某一位取反:
// 将 a 的第 b 位取反 ,最低位编号为 0
int flapBit(int a, int b) { return a ^ (1 << b); }

例4
给定一个长度为 n 的数列,请你求出数列中每个数的二进制表示中 1 的个数。
输入格式
第一行包含整数 n。
第二行包含 n 个整数,表示整个数列。
输出格式
共一行,包含 n 个整数,其中的第 i 个数表示数列中的第 i 个数的二进制表示中 1 的个数。
数据范围
1≤n≤100000
0≤数列中元素的值≤ (10^9) ≤数列中元素的值≤ (10^9)输入样例:
5 1 2 3 4 5输出样例:
1 1 2 1 2
#include <bits/stdc++.h>
using namespace std;
int good(int x)
{
int ans;
ans=x&(-x);
return ans;
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
int a,ans=0;
cin>>a;
while(a)
{
a-=good(a);
ans++;
}
cout<<ans<<" ";
}
cout<<endl;
return 0;
}
4____Hash函数
4.1____Hash的思想
Hash 的核心思想在于,将输入映射到一个值域较小、可以方便比较的范围。
我们定义一个把字符串映射到整数的函数 (f),这个 (f) 称为是 Hash 函数。
我们希望这个函数 (f) 可以方便地帮我们判断两个字符串是否相等。
具体来说,哈希函数最重要的性质可以概括为下面两条:
- 在 Hash 函数值不一样的时候,两个字符串一定不一样;
- 在 Hash 函数值一样的时候,两个字符串不一定一样(但有大概率一样,且我们当然希望它们总是一样的)。
4.2____字符串Hash
全称字符串前缀哈希法,把字符串变成一个p进制数字(哈希值),实现不同的字符串映射到不同的数字。
对形如 (X1X2X3⋯Xn−1Xn) 的字符串,采用字符的ascii 码乘上 P 的次方来计算哈希值。
映射公式: $ (X_1×P{n−1}+X_2×P{n−2}+⋯+X_{n−1}×P1+X_n×P0)modQ$
问题是比较不同区间的子串是否相同,就转化为对应的哈希值是否相同。
求一个字符串的哈希值就相当于求前缀和,求一个字符串的子串哈希值就相当于求部分和。
前缀和公式: $h[i+1]=h[i]×P+s[i] ,i∈[0,n−1] $为前缀和数组,s为字符串数组
区间和公式: (h[l,r]=h[r]−h[l−1]×P^{r−l+1})
区间和公式的理解: ABCDE 与 ABC 的前三个字符值是一样,只差两位,乘上P的二次方把 ABC 变为 ABC00,再用 ABCDE - ABC00 得到 DE 的哈希值。
例5
给定一个长度为 n 的字符串,再给定 m 个询问,每个询问包含四个整数 (l_1,r_1,l_2,r_2),请你判断 ([l_1,r_1][l_1,r_1]) 和 ([l_2,r_2][l_2,r_2]) 这两个区间所包含的字符串子串是否完全相同。
字符串中只包含大小写英文字母和数字。
输入格式
第一行包含整数 n 和 m,表示字符串长度和询问次数。
第二行包含一个长度为 n 的字符串,字符串中只包含大小写英文字母和数字。
接下来 m 行,每行包含四个整数 (l_1,r_1,l_2,r_2),表示一次询问所涉及的两个区间。
注意,字符串的位置从 1 开始编号。
输出格式
对于每个询问输出一个结果,如果两个字符串子串完全相同则输出
Yes,否则输出No。每个结果占一行。
数据范围
(1≤n,m≤10^5)
输入样例:
8 3 aabbaabb 1 3 5 7 1 3 6 8 1 2 1 2输出样例:
Yes No Yes
#include<iostream>
#include<cstdio>
#include<string>
using namespace std;
typedef unsigned long long ULL;
const int N = 1e5+5,P = 131;//131 13331
ULL h[N],p[N];
// h[i]前i个字符的hash值
// 字符串变成一个p进制数字,体现了字符+顺序,需要确保不同的字符串对应不同的数字
// P = 131 或 13331 Q=2^64,在99%的情况下不会出现冲突
// 使用场景: 两个字符串的子串是否相同
ULL query(int l,int r){
return h[r] - h[l-1]*p[r-l+1];
}
int main(){
int n,m;
cin>>n>>m;
string x;
cin>>x;
//字符串从1开始编号,h[1]为前一个字符的哈希值
p[0] = 1;
h[0] = 0;
for(int i=0;i<n;i++){
p[i+1] = p[i]*P;
h[i+1] = h[i]*P +x[i]; //前缀和求整个字符串的哈希值
}
while(m--){
int l1,r1,l2,r2;
cin>>l1>>r1>>l2>>r2;
if(query(l1,r1) == query(l2,r2)) printf("Yes
");
else printf("No
");
}
return 0;
}