[ACM]数列分块，ST表

ST表，数列分块

1____分块思想

1.1____引入

​ 我们之前学了线段树，但是这个东西是个很离谱的东西，代码量比较大。

​ 现在有就两种情况，一个是大材小用，一些很简单的问题，我们其实不用上线段树，另一个是线段树解决无法维护这些区间。

​ 但是，线段树也是很有用哈，我们学习很多的数据结构，是为了在适当的问题使用适当的数据结构来解决。

---

​ 现在我们来看这样一个问题，

给出一个长为n的数列，以及n个操作，操作涉及区间加法，单点查值。

(1le nle5e4)

​ 一看这不就是线段树板子题吗，单点修改单点查询，简单的很~

​ 确实，这是一道能用许多数据结构优化的经典题，可以用于不同数据结构训练。这里我们介绍一个更加简单的算法思想 分块。

1.2____数列分块

​ 对于每种数据结构，我个人认为最重要的三个问题为

1. 存储数据

2. 修改数据

3. 查询数据

   我们首先来看数列分块是如何存储数据的。
   

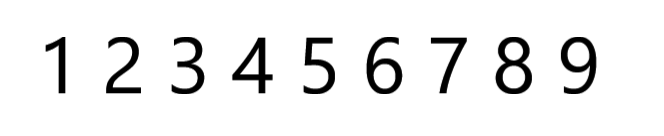
   对于这样一个数列，我们把他整体看成一个块，整个块的长度为9，之后我们把他分成大小相同的小块（只有在最后一个块可能大小和其他块不同）

   ​ 我们把整个块分为大小为$left lfloor sprt(n) ight floor $ 的小块

​ 如果 (n)​ 不是平方数的话，最后一个小块就不会满，但是这不影响我们之后的操作

---

​ 原理就是这样那么下面我们就来看看代码

储存与初始化

    int n;
    cin >> n;
    len = sqrt(n);

    for(int i = 1; i <= n ; i++){
        cin >> a[i];
        id[i] = (i - 1) / len + 1;
        s[ id[i] ] += a[i];
    }

这里我们用了3个数组

• a[]就是我们存储读入的数组
• id[]代表的是，对于每个a[]中的数，他是属于那个分块的
• s[]表示的是，每个小块的区间和为多少

---

我们来看一组读入数据为1 2 2 4的数据，每个数据值时怎么变化的

在这些操作完成后，我们现在可以快速查询一个块的区间和（虽然这个题并没有叫我们求区间和...后面的题的代码乱入了），以及查询对于某个下标，它属于那个块。

修改数据

​ 和线段树一样，修改同样是需要自己设计的，数据结构只是一个思想，数据如何操作最终还是要看自己如何设计的。

​ 一般我们对 l,r 区间进行修改时分为两种情况。

1. l,r在同一块中

   当l,r在同一块中的话，我们就直接暴力修改a[l-r]中的数据就好了。

2. l,r不在同一块中

   这个时候我们就需要引入一个tag[]数组，他的作用与线段树中lazy标记类似，但是在数列分块中，我们不会讲他push_down，我们在之后的查询中直接调用这个数组来进行处理就好

   tag[] 和区间和数组s[] 一样，他的每个元素存储的是整个区间的值。

   例如我要在这个区间都加上 2

   

   ​ 我们把查询区间分为三段

   • 以(l)开头的，前段非完整块（3）

   • 中间的数个，完整块（这里只有一个块[4,5,6]）

   • 以(r)结尾的，后段非完整块（7）

     对于非完整块，我们直接用暴力的方式去修改每一个数。

     对于完整块，我们直接对整块的tag[]数组进行修改，我们直接把值加到tag[]上就好了。

好了，修改的思想就是这样，这个问题的代码就是这样的。

void add(int l,int r,int c)
{
    int sid = id[l] , eid = id[r];	    /// sid , eid 为l的块编号以及r的块编号
    if( sid == eid ){                   /// 1.对应在同一块中的情况
        for(int i = l ;i <= r; i++){
            a[i] += c, s[sid] += c;
        }
        return ;
    }
    /// 2.对应在不同块中的情况
    /// 先修改非完整块的前端
    for(int i = l ; id[i] == sid ; i++) a[i] += c,s[ sid ] += c;
    /// 再对完整块进行操作
    for(int i = sid + 1 ; i < eid ; i++) tag[i] += c,s[ i ] += c * len;
    /// 最后对非完整块后端进行操作
    for(int i = r ; id[i] == eid ; i--) a[i] += c,s[eid] += c;
}

查询操作

​ 这个题的查询操作就是非常非常简单了，直接返回就好了~

int query(int x)
{
    return a[x] + tag[ id[x] ];
}

例1

数列分块入门 1

题目描述

给出一个长为 的数列，以及 个操作，操作涉及区间加法，单点查值。

输入格式

第一行输入一个数字 。

第二行输入 个数字，第 个数字为 ，以空格隔开。

接下来输入 行询问，每行输入四个数字 、、、，以空格隔开。

若 ，表示将位于 的之间的数字都加 。

若 ，表示询问 的值（ 和 忽略）。

输出格式

对于每次询问，输出一行一个数字表示答案。

样例

4
1 2 2 3
0 1 3 1
1 0 1 0
0 1 2 2
1 0 2 0

2
5

数据范围与提示

对于 (100%)的数据，(1le n le 50000)。

#include <bits/stdc++.h>
using namespace std;

const int N = 5e4 + 10;

int a[N],s[N],tag[N],len,id[N];

void add(int l,int r,int c)
{
    int sid = id[l] , eid = id[r];
    if( sid == eid ){
        for(int i = l ;i <= r; i++){
            a[i] += c, s[sid] += c;
        }
        return ;
    }

    for(int i = l ; id[i] == sid ; i++) a[i] += c,s[ sid ] += c;
    for(int i = sid + 1 ; i < eid ; i++) tag[i] += c,s[ i ] += c * len;
    for(int i = r ; id[i] == eid ; i--) a[i] += c,s[eid] += c;
}

int query(int x)
{
    return a[x] + tag[ id[x] ];
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n;
    cin >> n;
    len = sqrt(n);	/// 块的长度

    for(int i = 1; i <= n ; i++){
        cin >> a[i];
        id[i] = (i - 1) / len + 1;
        s[ id[i] ] += a[i];
    }

    for(int i = 0 ; i < n ; i++){
        int op,x,y,z;
        cin >> op >> x >> y >> z;
        if( op == 0 ){
            add(x,y,z);
        }else{
            cout << query(y) << endl;
        }
    }
    return 0;
}

1.3____数列分块小技巧

如果我知道了一个块的编号，如何求这个块的第一个点和最后一个点在a[]数组中的小标呢？

第一个数： (id - 1)*len + 1

最后一个数：id*len

---

现在我问你，你遇到这种题还想写线段树？

2____ST表

​ 说到ST表一个不得不说的话题就是倍增

​ 还是用我们一个经典的RMQ问题来引入ST表。

给一个长度为N的数组，求l,r区间的最小值

我们的ST表一般是开一个M[N]][31]的数组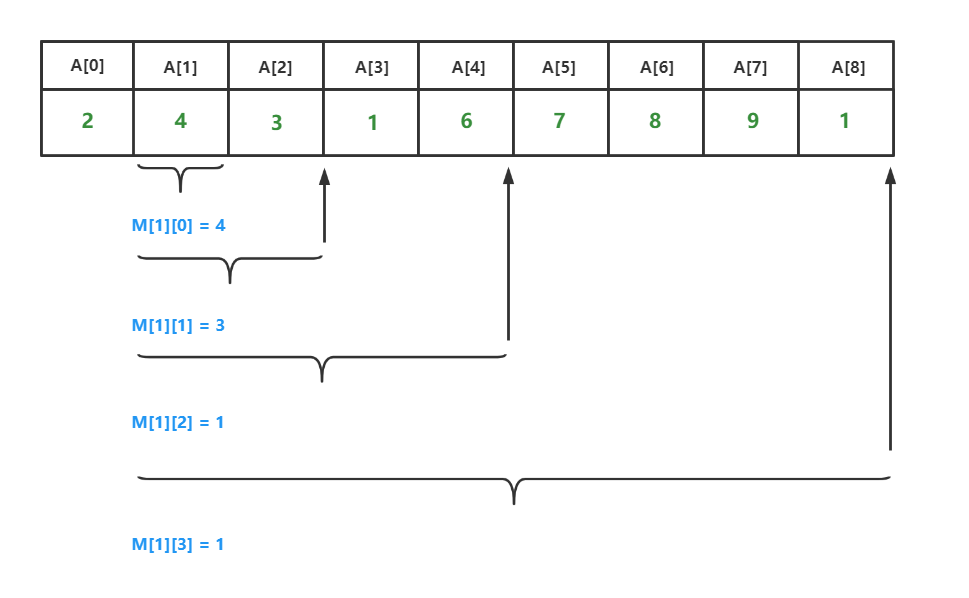

M[i][j] 表示从下标i 开始，长度为(2^j) 的子数组的最小值是多少

• M[1][0] 就代表，从下标为1的元素开始，(2^0=1)长度的这个区间的最小值为多少。
• M[1][3]就代表，从下标1的元素开始，(2^3=8) 长度的这个区间的最小值为多少。

2.1____ST表的DP预处理

​ 我们现在知道了ST表的每个下标的意义是什么，但是我们如何求得这个ST数组呢？

---

我们把M[i][j]对应的区间平均分成两端（M[i][j]对应的长度一定为偶数），从i到 (i+2^{j-1}-1)​ 为前一段， (i+2^{j-1}) 到 (i+2^j-1) 为后一段（长度都为(2^{j-1})），那么M[i][j]就是这两段的最小值中的最小值。

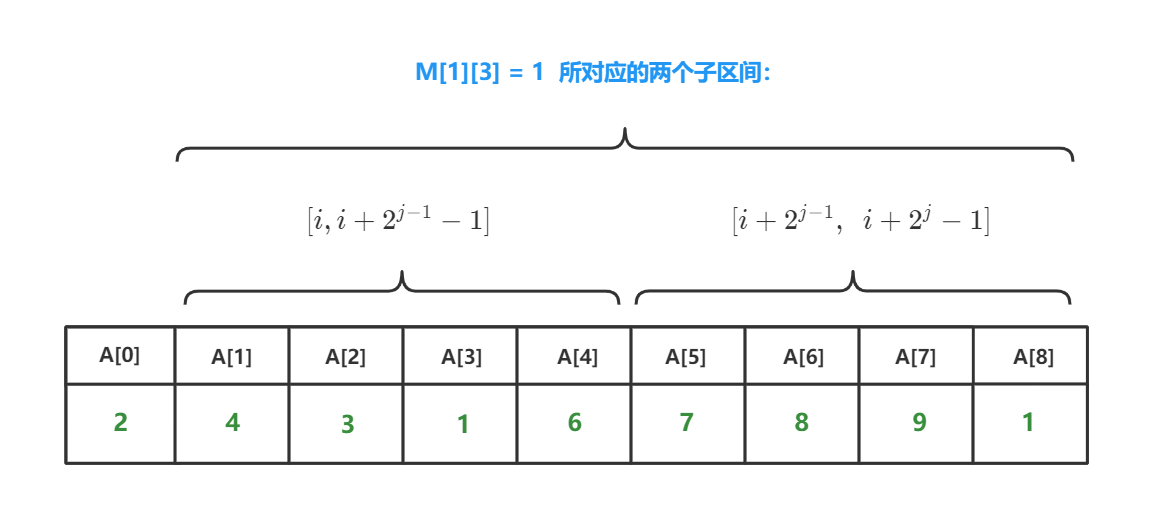
可得状态转移方程：

[M[i][j] = min(M[i][j-1],M[i+2^{j-1}][j-1]) ]

​ 在读入的时候初始化(j=0)​ 的情况cin >> M[i][0]

​ 这样我们就可以写出初始化函数了

void pre()
{
    for(int j = 1; j <= 31; j ++)
        for(int i = 1; i + (1<<j) - 1 <= n ; i++)
            a[i][j] = min( a[i][j-1],a[ i + (1 << (j-1)) ][j-1] );
}

2.2____ST表的查询操作

​ 我们通过选择两个完全能够覆盖区间[l,r]的块，取他们的最小值。设 $k = left lfloor log_2(j-i+1) ight floor $

[ans = min( M[i][k],M[j-2^k+1][k] ) ]

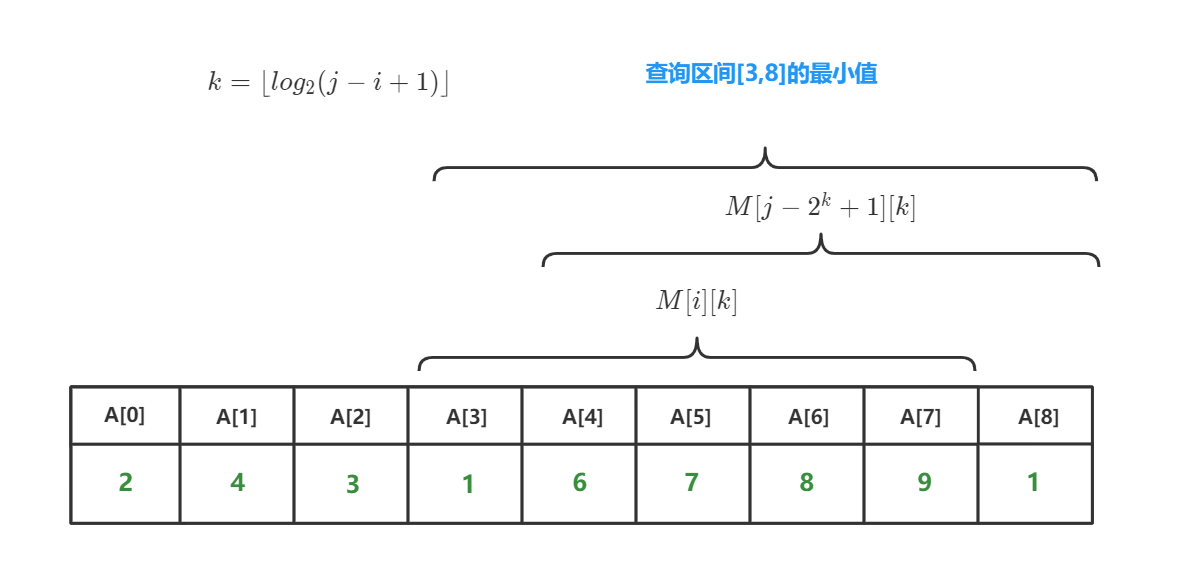
所以ST表算法的整体时间复杂度为：

• 预处理 (O(NlogN))
• 查询 $O(1) $

最终代码：

#include <bits/stdc++.h>
using namespace std;

int n,m;
const int N = 1e6+10;
int a[N][21];

inline void pre()
{
    for(int j = 1; j <= 21; j ++)
        for(int i = 1; i + (1<<j) - 1 <= n ; i++)
            a[i][j] = min( a[i][j-1],a[ i + (1 << (j-1)) ][j-1] );
}

inline int query(int l,int r)
{
    int k = log2(r-l+1);
    return min( a[l][k], a[ r-(1<<k) + 1 ][k] );
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1; i <= n ; i++) scanf("%d",&a[i][0]);

    pre();

    for(int i = 1 ; i + m - 1<= n ; i++){
         printf("%d
",query(i,i+m-1) );
    }

    return 0;
}

同时这个题也可以用分块来做

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6+10;
int mi[N];
int a[N];
int id[N];
int n,m,block;

int query(int l,int r)
{
    int sid = id[l],eid = id[r];
    int ans = 0x3f3f3f3f;
    if( sid == eid ){
        for(int i = l; i <= r; i++) ans = min(ans, a[i] );
        return ans;
    }

    for(int i = l ; id[i] == sid ; i++) ans = min(ans,a[i]);
    for(int i = sid + 1; i < eid ; i++) ans = min(ans,mi[i]);
    for(int i = (eid-1)*block + 1 ; i <=r ; i++ ) ans = min(ans,a[i]);
    return ans ;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n >> m ;
    block = sqrt(n);
    int len = (n-1)/block +1 ;
    for(int i = 1 ; i <= len; i ++){
        mi[i] = 0x3f3f3f3f;
    }

    for(int i = 1; i <= n ; i++){
        cin >> a[i];
        id[i] = ( i - 1 ) / block + 1;
        mi[ id[i] ] = min( mi[id[i]] , a[i] );
    }

    for(int i = 1; i + m - 1 <=  n; i ++){
        cout <<query(i,i+m-1) << endl;
    }

    return 0;
}

2.3____ST表的应用

​ 除 RMQ 以外，还有其它的“可重复贡献问题”。例如区间按位和、区间按位或、区间 GCD，ST 表都能高效地解决。虽然有的时候ST表和线段树解决问题的效率是一样的，但是代码量和debug的难易程度那是不能相提并论的。