Problem Description
In ACM_DIY, there is one master called “Lost”. As we know he is a “-2Dai”, which means he has a lot of money.
Well, Lost use Ipad and IPhone to reward the ones who solve the following problem.

In this problem, we define F( n ) as :
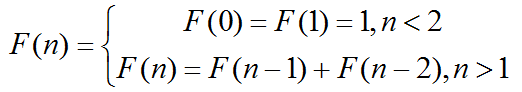
Then Lost denote a function G(a,b,n,p) as
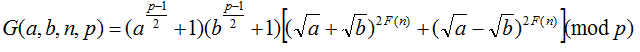
Here a, b, n, p are all positive integer!
If you could tell Lost the value of G(a,b,n,p) , then you will get one Ipad and one IPhone!

Well, Lost use Ipad and IPhone to reward the ones who solve the following problem.

In this problem, we define F( n ) as :
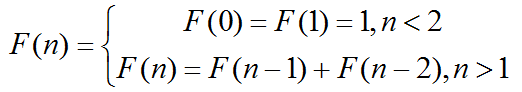
Then Lost denote a function G(a,b,n,p) as
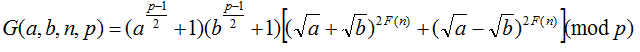
Here a, b, n, p are all positive integer!
If you could tell Lost the value of G(a,b,n,p) , then you will get one Ipad and one IPhone!
Input
The first line is one integer T indicates the number of the test cases. (T <= 100)
Then for every case, only one line containing 4 positive integers a, b, n and p.
(1 ≤a, b, n, p≤2*109 , p is an odd prime number and a,b < p.)
Then for every case, only one line containing 4 positive integers a, b, n and p.
(1 ≤a, b, n, p≤2*109 , p is an odd prime number and a,b < p.)
Output
Output one line,the value of the G(a,b,n,p) .
Sample Input
4
2 3 1 10007
2 3 2 10007
2 3 3 10007
2 3 4 10007
Sample Output
40
392
3880
9941
Author
AekdyCoin
Source
Recommend
notonlysuccess | We have carefully selected several similar problems for you: 3805 3800 3801 3803 3804
【分析】
不知道怎么回事...跟网上的程序对拍了好像没错,怎么过不了...应该是有些比较坑的点....
不错的一道题目,前面的两项不说了,后面的那一项可以把二次方弄进去,然后变成一个用韦达定理做一个逆运算得到特征方程。
然后就有递推式了,然后就可以矩阵加速了。
然后因为幂实在是太大了,然后上降幂大法,然后没了。
其实还涉及到二次剩余的理论,如果前面没有那两个式子答案就错了....因为刚好是那两个式子,让不能用降幂大法的情况变成0...

1 /* 2 五代李煜 3 《相见欢·林花谢了春红》 4 林花谢了春红,太匆匆。无奈朝来寒雨晚来风。 5 胭脂泪,相留醉,几时重。自是人生长恨水长东。 6 */ 7 #include <iostream> 8 #include <cstdio> 9 #include <ctime> 10 #include <cmath> 11 #include <algorithm> 12 #include <cstring> 13 #include <string> 14 #include <map> 15 #include <set> 16 #include <vector> 17 #define LOCAL 18 const int MAXN = 1000 + 10; 19 const int INF = 0x7fffffff; 20 using namespace std; 21 typedef long long ll; 22 ll mod;//代表取模的数字 23 ll check, a, b, n, p; 24 struct Matrix{ 25 ll num[5][5]; 26 //Matrix(){memset(num, 0, sizeof(num));} 27 }; 28 //为了防止和第一种矩阵乘法搞混 29 Matrix Mod(Matrix A, Matrix B, ll k){ 30 if (k == 0){//代表两种不同的乘法 31 Matrix c; 32 memset(c.num, 0, sizeof (c.num)); 33 for (ll i = 1; i <= 2; i++) 34 for (ll j = 1; j <= 2; j++) 35 for (ll k = 1; k <= 2; k++){ 36 ll tmp = (A.num[i][k] * B.num[k][j]); 37 if (check) tmp %= (p - 1); 38 c.num[i][j] += tmp; 39 if (check) c.num[i][j] %= (p - 1); 40 } 41 //一旦大于了p-1代表当前出现的斐波那契数列会大于phi(p),可以使用降幂大法 42 if ((c.num[1][1] + c.num[1][2]) > (p - 1)) check = 1; 43 return c; 44 }else if (k == 1){ 45 Matrix C; 46 memset(C.num, 0, sizeof(C.num)); 47 for (ll i = 1; i <= 2; i++) 48 for (ll j = 1; j <= 2; j++) 49 for (ll k = 1; k <= 2; k++) { 50 C.num[i][j] += (A.num[i][k] * B.num[k][j]) % p; 51 C.num[i][j] = ((C.num[i][j] % p) + p) % p; 52 } 53 return C; 54 } 55 } 56 //得到第x位的斐波那契数,也就是获得指数 57 Matrix Matrix_pow(Matrix A, ll x, ll k){ 58 if (x == 1) return A; 59 Matrix tmp = Matrix_pow(A, x / 2, k); 60 if (x % 2 == 0) return Mod(tmp, tmp, k); 61 else return Mod(Mod(tmp, tmp, k), A, k); 62 } 63 ll get(ll x){ 64 if (x == 0) return 1; 65 else if (x == 1) return 1; 66 Matrix A, B; 67 A.num[1][1] = 1; A.num[1][2] = 1; 68 A.num[2][1] = 1; A.num[2][2] = 0; 69 x--;//为真实的需要乘的次数 70 if (x == 0) return 1; 71 B = Matrix_pow(A, x, 0); 72 if (B.num[1][1] + B.num[1][2] > (p - 1)) check = 1; 73 if (check == 0) return B.num[1][1] + B.num[1][2]; 74 else return (B.num[1][1] + B.num[1][2]) % (p - 1) + p - 1; 75 } 76 //有了a,b,pos就可进行矩阵加速了 77 ll cal(ll a, ll b, ll pos){ 78 if (pos == 0) return 2 % p; 79 else if (pos == 1) return (2 * (a + b)) % p; 80 Matrix A; 81 A.num[1][1] = (2 * (a + b)) % p; A.num[1][2] = (((-(a - b) * (a - b)) % p) + p) % p; 82 A.num[2][1] = 1; A.num[2][2] = 0; 83 pos--; 84 Matrix B; 85 B = Matrix_pow(A, pos, 1); 86 return (B.num[1][1] * A.num[1][1]) % p + (B.num[1][2] * 2) % p; 87 } 88 ll pow(ll a, ll b){ 89 if (b == 0) return 1 % p; 90 if (b == 1) return a % p; 91 ll tmp = pow(a, b / 2); 92 if (b % 2 == 0) return (tmp * tmp) % p; 93 else return (((tmp * tmp) % p) * a) % p; 94 } 95 96 int main(){ 97 int T; 98 scanf("%d", &T); 99 while (T--){ 100 //for (int i = 1; i ,=) 101 scanf("%lld%lld%lld%lld", &a, &b, &n, &p); 102 check = 0;//判断f(n)是否大于p 103 ll pos = get(n); 104 ll Ans = cal(a, b, pos); 105 ll f1, f2; 106 f1 = (pow(a, (p - 1) / 2) + 1) % p; 107 f2 = (pow(b, (p - 1) / 2) + 1) % p; 108 Ans = (((f1 * f2) % p) * Ans) % p; 109 printf("%lld ", Ans); 110 } 111 //p = 0x7fffffff; 112 //printf("%lld", get(5)); 113 //for (int i = 0; i <= 10; i++) printf("%lld ", get(i)); 114 return 0; 115 }
