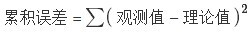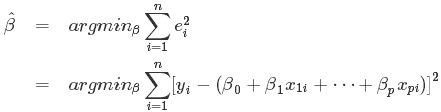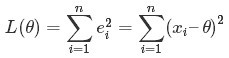本文总结ML面试常见的问题集
转载来源:https://blog.csdn.net/v_july_v/article/details/78121924
61、说说共轭梯度法?
@wtq1993,http://blog.csdn.net/wtq1993/article/details/51607040
共轭梯度法是介于梯度下降法(最速下降法)与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了梯度下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hessian矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。在各种优化算法中,共轭梯度法是非常重要的一种。其优点是所需存储量小,具有逐步收敛性,稳定性高,而且不需要任何外来参数。

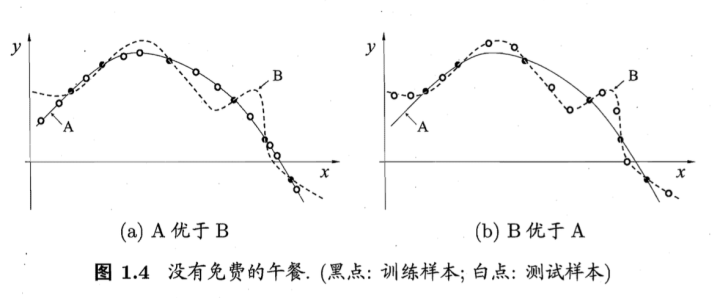
没有免费的午餐定理:
对于训练样本(黑点),不同的算法A/B在不同的测试样本(白点)中有不同的表现,这表示:对于一个学习算法A,若它在某些问题上比学习算法 B更好,则必然存在一些问题,在那里B比A好。
也就是说:对于所有问题,无论学习算法A多聪明,学习算法 B多笨拙,它们的期望性能相同。
但是:没有免费午餐定力假设所有问题出现几率相同,实际应用中,不同的场景,会有不同的问题分布,所以,在优化算法时,针对具体问题进行分析,是算法优化的核心所在。
我们口头中经常说:一般来说,平均来说。如平均来说,不吸烟的健康优于吸烟者,之所以要加“平均”二字,是因为凡事皆有例外,总存在某个特别的人他吸烟但由于经常锻炼所以他的健康状况可能会优于他身边不吸烟的朋友。而最小二乘法的一个最简单的例子便是算术平均。
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。用函数表示为:
使误差「所谓误差,当然是观察值与实际真实值的差量」平方和达到最小以寻求估计值的方法,就叫做最小二乘法,用最小二乘法得到的估计,叫做最小二乘估计。当然,取平方和作为目标函数只是众多可取的方法之一。
最小二乘法的一般形式可表示为:
有效的最小二乘法是勒让德在 1805 年发表的,基本思想就是认为测量中有误差,所以所有方程的累积误差为
我们求解出导致累积误差最小的参数即可:
勒让德在论文中对最小二乘法的优良性做了几点说明:
- 最小二乘使得误差平方和最小,并在各个方程的误差之间建立了一种平衡,从而防止某一个极端误差取得支配地位
- 计算中只要求偏导后求解线性方程组,计算过程明确便捷
- 最小二乘可以导出算术平均值作为估计值
对于最后一点,从统计学的角度来看是很重要的一个性质。推理如下:假设真值为 , 为n次测量值, 每次测量的误差为,按最小二乘法,误差累积为
求解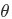
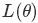
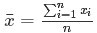
由于算术平均是一个历经考验的方法,而以上的推理说明,算术平均是最小二乘的一个特例,所以从另一个角度说明了最小二乘方法的优良性,使我们对最小二乘法更加有信心。
最小二乘法的原理之一:当估计误差服从正态分布时,最小二乘法等同于极大似然估计。 如果 y = f(x) + e, 其中y 是目标值,f(x)为估计值,e为误差项。如果e服从正态分布,那么 细节可以看:https://www.zhihu.com/question/20447622/answer/209839263,而由于中心极限定理的原因,很多误差分布确实服从正态分布,这也是最小二乘法能够十分有效的一个原因。
最小二乘法发表之后很快得到了大家的认可接受,并迅速的在数据分析实践中被广泛使用。不过历史上又有人把最小二乘法的发明归功于高斯,这又是怎么一回事呢。高斯在1809年也发表了最小二乘法,并且声称自己已经使用这个方法多年。高斯发明了小行星定位的数学方法,并在数据分析中使用最小二乘方法进行计算,准确的预测了谷神星的位置。
对了,最小二乘法跟SVM有什么联系呢?请参见《支持向量机通俗导论(理解SVM的三层境界)》。
这里是一些关键点:Python是解释型语言。这意味着不像C和其他语言,Python运行前不需要编译。其他解释型语言包括PHP和Ruby。
- Python是动态类型的,这意味着你不需要在声明变量时指定类型。你可以先定义
x=111,然后x=”I’m a string”。 - Python是面向对象语言,所有允许定义类并且可以继承和组合。Python没有访问访问标识如在C++中的
public,private, 这就非常信任程序员的素质,相信每个程序员都是“成人”了~ - 在Python中,函数是一等公民。这就意味着它们可以被赋值,从其他函数返回值,并且传递函数对象。类不是一等公民。
- 写Python代码很快,但是跑起来会比编译型语言慢。幸运的是,Python允许使用C扩展写程序,所以瓶颈可以得到处理。Numpy库就是一个很好例子,因为很多代码不是Python直接写的,所以运行很快。
- Python使用场景很多 – web应用开发、大数据应用、数据科学、人工智能等等。它也经常被看做“胶水”语言,使得不同语言间可以衔接上。
- Python能够简化工作 ,使得程序员能够关心如何重写代码而不是详细看一遍底层实现。
答:从三个方面来说,一对象的引用计数机制,二垃圾回收机制,三内存池机制
一、对象的引用计数机制
Python内部使用引用计数,来保持追踪内存中的对象,所有对象都有引用计数。
引用计数增加的情况:
1,一个对象分配一个新名称
2,将其放入一个容器中(如列表、元组或字典)
引用计数减少的情况:
1,使用del语句对对象别名显示的销毁
2,引用超出作用域或被重新赋值
sys.getrefcount( )函数可以获得对象的当前引用计数
多数情况下,引用计数比你猜测得要大得多。对于不可变数据(如数字和字符串),解释器会在程序的不同部分共享内存,以便节约内存。
二、垃圾回收
1,当一个对象的引用计数归零时,它将被垃圾收集机制处理掉。
2,当两个对象a和b相互引用时,del语句可以减少a和b的引用计数,并销毁用于引用底层对象的名称。然而由于每个对象都包含一个对其他对象的应用,因此引用计数不会归零,对象也不会销毁。(从而导致内存泄露)。为解决这一问题,解释器会定期执行一个循环检测器,搜索不可访问对象的循环并删除它们。
三、内存池机制
Python提供了对内存的垃圾收集机制,但是它将不用的内存放到内存池而不是返回给操作系统。
1,Pymalloc机制。为了加速Python的执行效率,Python引入了一个内存池机制,用于管理对小块内存的申请和释放。
2,Python中所有小于256个字节的对象都使用pymalloc实现的分配器,而大的对象则使用系统的malloc。
3,对于Python对象,如整数,浮点数和List,都有其独立的私有内存池,对象间不共享他们的内存池。也就是说如果你分配又释放了大量的整数,用于缓存这些整数的内存就不能再分配给浮点数。
答:
1,使用set函数,set(list)
2,使用字典函数,
>>>a=[1,2,4,2,4,5,6,5,7,8,9,0]
>>> b={}
>>>b=b.fromkeys(a) ##创建一个新字典,以序列 seq 中元素做字典的键,value 为字典所有键对应的初始值。
>>>c=list(b.keys())
>>> c
@Tom_junsong,http://www.cnblogs.com/tom-gao/p/6645859.html
a.sort()
last=a[-1]
for i in range(len(a)-2,-1,-1):
if last==a[i]:
del a[i]
else:last=a[i]
print(a)
答:random模块
随机整数:random.randint(a,b):返回随机整数x,a<=x<=b
random.randrange(start,stop,[,step]):返回一个范围在(start,stop,step)之间的随机整数,不包括结束值。
随机实数:random.random( ):返回0到1之间的浮点数
random.uniform(a,b):返回指定范围内的浮点数。更多Python笔试面试题请看:http://python.jobbole.com/85231/
对于给定的输入X,由f(X)给出相应的输出Y,这个输出的预测值f(X)与真实值Y可能一致也可能不一致(要知道,有时损失或误差是不可避免的),用一个损失函数来度量预测错误的程度。损失函数记为L(Y, f(X))。
常用的损失函数有以下几种(基本引用自《统计学习方法》):
如此,SVM有第二种理解,即最优化+损失最小,或如@夏粉_百度所说“可从损失函数和优化算法角度看SVM,boosting,LR等算法,可能会有不同收获”。关于SVM的更多理解请参考:支持向量机通俗导论(理解SVM的三层境界)
Logistic回归目的是从特征学习出一个0/1分类模型,而这个模型是将特性的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。因此,使用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。
假设函数
 的图像是
的图像是 从而,当我们要判别一个新来的特征属于哪个类时,只需求 即可,若
即可,若 大于0.5就是y=1的类,反之属于y=0类。
大于0.5就是y=1的类,反之属于y=0类。
此外, 只和
只和 有关,
有关, >0,那么
>0,那么 ,而g(z)只是用来映射,真实的类别决定权还是在于
,而g(z)只是用来映射,真实的类别决定权还是在于 。再者,当
。再者,当 时,
时, =1,反之
=1,反之 =0。如果我们只从
=0。如果我们只从 出发,希望模型达到的目标就是让训练数据中y=1的特征
出发,希望模型达到的目标就是让训练数据中y=1的特征 ,而是y=0的特征
,而是y=0的特征 。Logistic回归就是要学习得到
。Logistic回归就是要学习得到 ,使得正例的特征远大于0,负例的特征远小于0,而且要在全部训练实例上达到这个目标。
,使得正例的特征远大于0,负例的特征远小于0,而且要在全部训练实例上达到这个目标。
接下来,尝试把logistic回归做个变形。首先,将使用的结果标签y = 0和y = 1替换为y = -1,y = 1,然后将 (
( )中的
)中的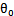
 替换为
替换为 (即
(即 )。如此,则有了
)。如此,则有了 。也就是说除了y由y=0变为y=-1外,线性分类函数跟logistic回归的形式化表示
。也就是说除了y由y=0变为y=-1外,线性分类函数跟logistic回归的形式化表示 没区别。
没区别。
进一步,可以将假设函数 中的g(z)做一个简化,将其简单映射到y=-1和y=1上。映射关系如下:
中的g(z)做一个简化,将其简单映射到y=-1和y=1上。映射关系如下:
最后补充一点,正态分布的极大似然估计 如果n维空间中两组点的分布各自服从多元正态分布,那么逻辑回归就等价于利用极大似然估计来对空间中的点进行分类。细节可以参考:http://blog.sciencenet.cn/blog-508318-633085.html。