PAT Advanced A1021 Deepest Root (25) [图的遍历，DFS，计算连通分量的个数，BFS，并查集]

题目

A graph which is connected and acyclic can be considered a tree. The height of the tree depends on the selected root. Now you are supposed to find the root that results in a highest tree. Such a root is called the deepest root.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (<=10000) which is the number of nodes, and hence the nodes are numbered from 1 to N. Then N-1 lines follow, each describes an edge by given the two adjacent nodes’ numbers.
Output Specification:
For each test case, print each of the deepest roots in a line. If such a root is not unique, print them in increasing order of their numbers. In case that the given graph is not a tree, print “Error: K components” where K is the number of connected components in the graph.
Sample Input 1:
5
1 2
1 3
1 4
2 5
Sample Output 1:
3
4
5
Sample Input 2:
5
1 3
1 4
2 5
3 4
Sample Output 2:
Error: 2 components

题目分析

已知图的顶点N和边N-1，判断所给图是否是一棵树，如果是，查找并打印最高树的所有根节点（从小到大）

• 判断图为树有两个条件：只有一个连通分量（否则为森林）；无环（已知顶点数为N，边为N-1的连通图一定是树）
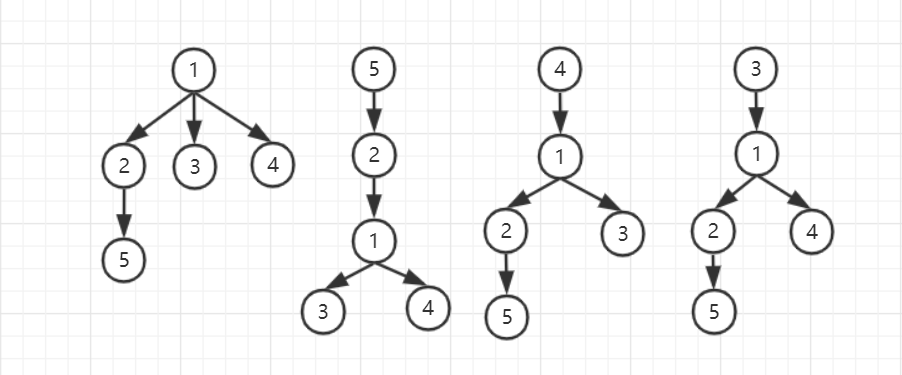
• 最高树的所有根节点，其含义可以从样例中推导得出（起始顶点不同，寻找出的最高树不同）

解题思路

1. 存储顶点和边

• 邻接表
• 邻接矩阵

2. 计算连通分量个数

连通分量等于1时，满足条件

• DFS
• BFS
• 并查集

3. 查找最大高度树的根节点

• 任意取一个顶点，求其能到达的最远的节点集合A，如测试样例1中：取1，可以得到5,3,4
• 任取取A集合中一个顶点，求其能到达的最远的节点集合B，如取A集合中3，可以得到4,5
• 集合A和集合B的并集去重排序，即为答案

Code

Code 01（邻接矩阵 并查集）

#include <iostream>
#include <vector>
#include <set>
using namespace std;
const int maxn=10010;
vector<int> g[maxn],temp; //邻接表 存储边
set<int> vs; // 存储所有满足条件的 the deepest roots
int maxh,n,father[maxn],vis[maxn];
/*
	并查集判断连通分量树
	两次dfs求the deepest root
*/
int init() { /* 并查集 初始化 */
	for(int i=1; i<=n; i++)father[i]=i;
}
int find(int x) { /* 并查集 查 */
	int a = x;
	while(x!=father[x]) {
		x=father[x];
	}
	while(a!=father[a]) { // 路径压缩
		int temp=a;
		a=father[a];
		father[a]=x;
	}
	return x;
}
void Union(int a,int b) { /* 并查集 并 */
	int fa=find(a);
	int fb=find(b);
	if(fa<fb)father[fb]=fa;
	else father[fa]=fb;
}
void dfs(int a, int h) { /* dfs */
	vis[a]=1;
	if(h>maxh) {
		temp.clear();
		temp.push_back(a); // the deepest root
		maxh=h;
	} else if(h==maxh) 
		temp.push_back(a);
	for(int i=0; i<g[a].size(); i++) {
		if(vis[g[a][i]]==0)
			dfs(g[a][i],h+1);
	}
}
void pts() {
	for(int i=0; i<temp.size(); i++)
		vs.insert(temp[i]);
}
int main(int argc,char * argv[]) {
	int a,b;
	scanf("%d",&n);
	init();
	for(int i=1; i<=n-1; i++) {
		scanf("%d %d",&a,&b);
		g[a].push_back(b);
		g[b].push_back(a);
		Union(a,b);
	}
	// 统计连通分量数
	for(int i=1; i<=n; i++) {
		vs.insert(find(i));
	}
	if(vs.size()>1) {
		printf("Error: %d components",vs.size());
		return 0;
	}
	vs.clear(); //vs重置，方便下面使用 
	dfs(1,1); // 第一次dfs，任意取一个顶点，获取最深根集合A
	pts(); //将集合A存入set
	fill(vis,vis+maxn,0); //重置vis访问标记数组 
	//maxh=0; //无需重置maxh，因为第一轮得到的maxh即为最高树高度，第二轮中h==maxh时添加剩余的the deepest root 
	dfs(temp[0],1);// 第二次dfs，从集合A中任取一个顶点，获取最深根集合B
	pts(); //将集合B存入set 
	for(set<int>::iterator it=vs.begin(); it!=vs.end(); it++) { //set默认从小到大，A+B去重即为结果
		printf("%d
",*it);
	}
	return 0;
}

Code 02（邻接矩阵 DFS）

#include <iostream>
#include <vector>
#include <set>
using namespace std;
const int maxn=10010;
vector<int> g[maxn],temp; //邻接表 存储边
set<int> vs; // 存储所有满足条件的 the deepest roots
int n,maxh,vis[maxn];
/*
	第一次dfs 求连通分量，求the deepest root集合A 
	第二次dfs 求the deepest root集合B
	集合A+B，去重排序 即为答案 
*/
void dfs(int a, int h) { /* dfs */
	vis[a]=1;
	if(h>maxh) {
		temp.clear();
		temp.push_back(a); // the deepest root
		maxh=h;
	} else if(h==maxh) 
		temp.push_back(a);
	for(int i=0; i<g[a].size(); i++) {
		if(vis[g[a][i]]==0)
			dfs(g[a][i],h+1);
	}
}
void pts() {
	for(int i=0; i<temp.size(); i++)
		vs.insert(temp[i]);
}
int main(int argc,char * argv[]) {
	int a,b;
	scanf("%d",&n);
	for(int i=1; i<=n-1; i++) {
		scanf("%d %d",&a,&b);
		g[a].push_back(b);
		g[b].push_back(a);
	}
	// 统计连通分量数
	int cnt=0;
	for(int i=1; i<=n; i++) {
		if(vis[i]==0){
			dfs(i,0); 
			pts(); //将集合A存入set
			cnt++;
		}
	}
	if(cnt>1) {
		printf("Error: %d components",cnt);
		return 0;
	}
	fill(vis,vis+maxn,0); //重置vis访问标记数组 
	//maxh=0; //无需重置maxh，因为第一轮得到的maxh即为最高树高度，第二轮中h==maxh时添加剩余的the deepest root 
	dfs(temp[0],1);// 第二次dfs，从集合A中任取一个顶点，获取最深根集合B
	pts(); //将集合B存入set 
	for(set<int>::iterator it=vs.begin(); it!=vs.end(); it++) { //set默认从小到大，A+B去重即为结果
		printf("%d
",*it);
	}
	return 0;
}

Code 03（邻接矩阵 BFS）

#include <iostream>
#include <vector>
#include <set>
#include <queue>
using namespace std;
const int maxn=10010;
vector<int> g[maxn],temp; //邻接表 存储边
set<int> vs; // 存储所有满足条件的 the deepest roots
int n,maxh,vis[maxn];
struct node {
	int v;
	int h;
};
/*
	第一次bfs 求连通分量，求the deepest root集合A
	第二次bfs 求the deepest root集合B
	集合A+B，去重排序 即为答案
*/
void bfs(int a) { /* dfs */
	vis[a]=1;
	queue<node> q;
	q.push({a,0});
	while(!q.empty()) {
		node now = q.front();
		q.pop();
		if(now.h>maxh) {
			temp.clear();
			temp.push_back(now.v); // the deepest root
			maxh=now.h;
		} else if(now.h==maxh)
			temp.push_back(now.v);
		for(int i=0; i<g[now.v].size(); i++)
			if(vis[g[now.v][i]]==0){
				q.push({g[now.v][i],now.h+1});
				vis[g[now.v][i]]=1;
			}
	}
}
void pts() {
	for(int i=0; i<temp.size(); i++)
		vs.insert(temp[i]);
}
int main(int argc,char * argv[]) {
	int a,b;
	scanf("%d",&n);
	for(int i=1; i<=n-1; i++) {
		scanf("%d %d",&a,&b);
		g[a].push_back(b);
		g[b].push_back(a);
	}
	// 统计连通分量数
	int cnt=0;
	for(int i=1; i<=n; i++) {
		if(vis[i]==0) {
			bfs(i);
			pts(); //将集合A存入set
			cnt++;
		}
	}
	if(cnt>1) {
		printf("Error: %d components",cnt);
		return 0;
	}
	fill(vis,vis+maxn,0); //重置vis访问标记数组
	//maxh=0; //无需重置maxh，因为第一轮得到的maxh即为最高树高度，第二轮中h==maxh时添加剩余的the deepest root
	bfs(temp[0]);// 第二次dfs，从集合A中任取一个顶点，获取最深根集合B
	pts(); //将集合B存入set
	for(set<int>::iterator it=vs.begin(); it!=vs.end(); it++)  //set默认从小到大，A+B去重即为结果
		printf("%d
",*it);
	return 0;
}

Code 04（邻接表 DFS）

#include <iostream>
#include <vector>
#include <set>
using namespace std;
const int maxn=10010;
vector<int> temp; //邻接表 存储边
set<int> vs; // 存储所有满足条件的 the deepest roots
int n,maxh,vis[maxn],g[maxn][maxn];
/*
	第一次dfs 求连通分量，求the deepest root集合A
	第二次dfs 求the deepest root集合B
	集合A+B，去重排序 即为答案
*/
void dfs(int a, int h) { /* dfs */
	vis[a]=1;
	if(h>maxh) {
		temp.clear();
		temp.push_back(a); // the deepest root
		maxh=h;
	} else if(h==maxh)
		temp.push_back(a);
	for(int i=1; i<maxn; i++)
		if(g[a][i]==1 && vis[i]==0)
			dfs(i,h+1);
}
void pts() {
	for(int i=0; i<temp.size(); i++)
		vs.insert(temp[i]);
}
int main(int argc,char * argv[]) {
	int a,b;
	scanf("%d",&n);
	for(int i=1; i<=n-1; i++) {
		scanf("%d %d",&a,&b);
		g[a][b]=1;
		g[b][a]=1;
	}
	// 统计连通分量数
	int cnt=0;
	for(int i=1; i<=n; i++) {
		if(vis[i]==0) {
			dfs(i,0);
			pts(); //将集合A存入set
			cnt++;
		}
	}
	if(cnt>1) {
		printf("Error: %d components",cnt);
		return 0;
	}
	fill(vis,vis+maxn,0); //重置vis访问标记数组
	//maxh=0; //无需重置maxh，因为第一轮得到的maxh即为最高树高度，第二轮中h==maxh时添加剩余的the deepest root
	dfs(temp[0],1);// 第二次dfs，从集合A中任取一个顶点，获取最深根集合B
	pts(); //将集合B存入set
	for(set<int>::iterator it=vs.begin(); it!=vs.end(); it++) { //set默认从小到大，A+B去重即为结果
		printf("%d
",*it);
	}
	return 0;
}

Code 05（邻接表 BFS）

#include <iostream>
#include <vector>
#include <set>
#include <queue>
using namespace std;
const int maxn=10010;
vector<int> temp; //邻接表 存储边
set<int> vs; // 存储所有满足条件的 the deepest roots
int n,maxh,vis[maxn],g[maxn][maxn];
struct node {
	int v;
	int h;
};
/*
	第一次bfs 求连通分量，求the deepest root集合A
	第二次bfs 求the deepest root集合B
	集合A+B，去重排序 即为答案
*/
void bfs(int a) { /* dfs */
	vis[a]=1;
	queue<node> q;
	q.push({a,0});
	while(!q.empty()) {
		node now = q.front();
		q.pop();
		if(now.h>maxh) {
			temp.clear();
			temp.push_back(now.v); // the deepest root
			maxh=now.h;
		} else if(now.h==maxh)
			temp.push_back(now.v);
		for(int i=1; i<maxn; i++)
			if(g[now.v][i]==1 && vis[i]==0){
				q.push({i,now.h+1});
				vis[i]=1;
			}
	}
}
void pts() {
	for(int i=0; i<temp.size(); i++)
		vs.insert(temp[i]);
}
int main(int argc,char * argv[]) {
	int a,b;
	scanf("%d",&n);
	for(int i=1; i<=n-1; i++) {
		scanf("%d %d",&a,&b);
		g[a][b]=1;
		g[b][a]=1;
	}
	// 统计连通分量数
	int cnt=0;
	for(int i=1; i<=n; i++) {
		if(vis[i]==0) {
			bfs(i);
			pts(); //将集合A存入set
			cnt++;
		}
	}
	if(cnt>1) {
		printf("Error: %d components",cnt);
		return 0;
	}
	fill(vis,vis+maxn,0); //重置vis访问标记数组
	//maxh=0; //无需重置maxh，因为第一轮得到的maxh即为最高树高度，第二轮中h==maxh时添加剩余的the deepest root
	bfs(temp[0]);// 第二次dfs，从集合A中任取一个顶点，获取最深根集合B
	pts(); //将集合B存入set
	for(set<int>::iterator it=vs.begin(); it!=vs.end(); it++)  //set默认从小到大，A+B去重即为结果
		printf("%d
",*it);
	return 0;
}