排序算法概述
排序的分类
排序的两种分类
1、内部排序:将所需要的数据先加到内存中,然后进行排序
2、外部排序:数据量无法一次性全部加载到内存中,需要借助外部存储器进行排序
常见的排序算法分类
内部排序
1、插入
- 直接插入排序
- 希尔排序
2、选择
- 简单选择排序
- 堆排序(在二叉树讲解完之后再讲)
3、交换
- 冒泡排序
- 快速排序
4、归并
5、基数(桶排序升级版)
算法的时间复杂度
度量一个算法执行时间的两种方法
1、事后统计法:程序先运行,然后根据程序运行的时间来判断哪个算法更快
2、事前估算法:通过分析某个算法的时间复杂度来判断哪个算法更优
事后统计法与很多因素有关系,比如计算机的硬件,时间可能太长等等。。。
所以我们需要事前估算法
时间频度
一个算法花费的时间与语句的执行次数成正比例,哪个算法中语句执行次数多,它花费的时间就多
一个算法中的语句执行次数成为语句频度(或者时间频度),记为T(n)
举例:
计算1~100所有数字之和,有两种算法
int total = 0;
int end = 100;
//算法1
for(int i=1;i<=end;i++){
total+=i;
}
//算法2
total = (1+end)*end/2
算法1的时间频度T(n)=n+1;因为要进行end+1次判断,end就是n,所以是n+1,简写为T(n+1)
算法2的T(n)=1;因为只需要执行一次就知道了结果,简写为T(1)
时间频度的注意事项
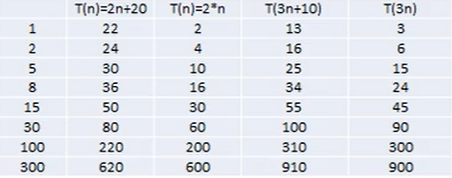
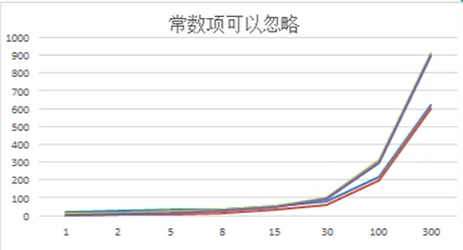
1、忽略常数项
我们可以看到,前两个为一组和后两个为一组,这两组随着n的无限增大,在自己组内的差距其实是在无限减小的
所以我们可以明白:常数项是可以忽略不计的,比如第一组里的20,第二组里的10
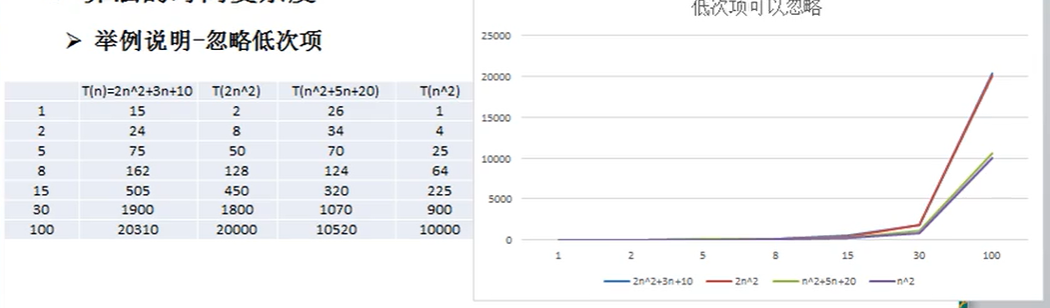
2、忽略低次项
前两个为一组,后两个为一组
我们可以看到,随着数值的不断增大,各自组内的数据也在无限接近
可以忽略3n+10和5n+20
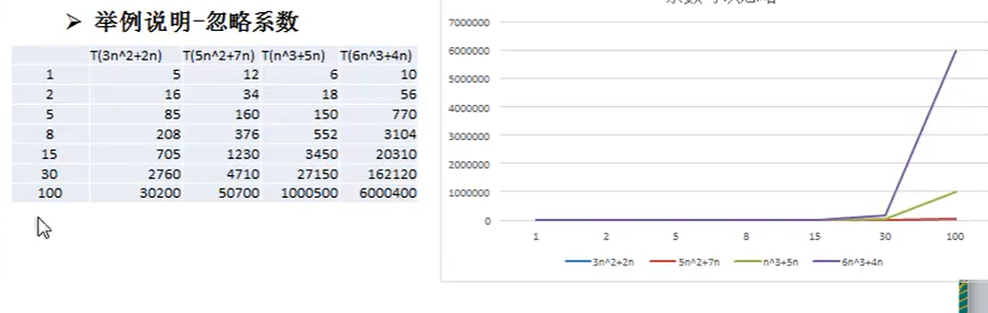
3、忽略系数
随着n的变大
5n^2+7n 和 3n^2+2n逐渐重合,说明这种情况下5和3可以忽略
n^3+5n 和 6n^3+4n逐渐分离
在二次方的时候,5和3这两个系数最后在不断重合
在三次方的时候,6和1却在不断分离
因为幂的不同,系数的改变出现了不同的结果。所以说,系数不重要,多少次幂才重要
时间复杂度
1、一般情况下,算法中的基本操作语句的重复执行次数是问题规模n的某个函数,用T(n)表示【时间频度】,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)趋近于不等于零的常数,则称f(n)是T(n)的同数量级函数。
记做T(n)=(f(n)),称O(f(n))为算法的渐进时间复杂度,简称时间复杂度
举个例子
例1:
现在时间频度为T(n) = n+1,我们知道,系数,常数是可以忽略的,那么就相当于n
现在只要有一个函数f(n),满足T(n)/f(n)无限趋近于非零整数,那么O(f(n))就是时间复杂度
让n/f(n)的这个f(n)自然就是n
那么算下来,O(f(n))=n
也就是说,我们找时间复杂度,最后都要寻找O(f(n)),这个f(n)是我们自己找的
例2:
现在有T(n)=n2+7n+6 ,我们知道,系数,常数,低次项是可以忽略的,所以就是n2
现在我们要得到时间复杂度,就要找一个T(n)/f(n)不为0的常数,那么f(n)=n2
所以时间复杂度为O(n2)
所以我们的推断有以下几个步骤,就拿T(n)=n2+7n+6来说
1、用常数1替代函数的所有加法常数:T(n)=n2+7n+1
2、只保留最高阶项:T(n)=n2
3、将最高阶项的系数改为1:这里已经是1了,所以不需要改
4、得出时间复杂度:O(n2)
常见的时间复杂度

时间复杂度由小到大:
常数阶<对数阶<线性阶<线性对数阶<平方阶<立方阶<k次方阶<指数阶<n次阶
对数阶不一定非得是2,也可能是3,4,....
要极力避免我们程序中出现指数阶的时间复杂度,更不用说n的n次阶了,这个图上直接都没有,直接爆炸了
举几个例子
1、常数阶
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;
不管i和j是什么数字,它执行的时间不会随着数字的增长而增长,从始至终就是五条语句
2、对数阶
int i = 1;
while(i<n){
i = i * 2;
}
N=ax,即a的x次方等于N(其中a>0且a!=1),那么数x叫做以a为底的对数,记做x=logaN
在这个while循环中,每次都将i乘2,乘完之后,i就是i乘2的一次次方,2的二次方,2的三次方,....,直到第x次为2的x次方等于n(这个x此时不一定是整数),然后大于n,退出循环
也就是说2的x次方等于n,也就是x=logan
3、线性阶
for(i=1; i<n; ++i){
j = i;
j++;
}
里面的for循环会执行n遍,因此消耗的时间是随着n变化的
4、线性对数阶
for(m=1; m<n; m++){
i=1;
while(i < n){
i = i * 2;
}
}
将时间复杂度为对数阶的代码循环n遍,也就是n*O(log2N),也就是O(nlog2N)
5、平方阶
for(x=1; i<=n; x++){
for(i=1; i<=n; i++){
j = i;
j++;
}
}
也就是双层for循环
参考上面的几个时间复杂度,我们可以知道,从最里面开始看起,然后依次向外看
先找好最里面的时间复杂度,然后外面套里面即可
平均时间复杂度和最坏时间复杂度
平均时间复杂度
是指所有可能的情况输入实例平均到等概率出现的情况下,这个算法所运行的时间
最坏时间复杂度
是指最坏情况下发生的时间复杂度
我们一般讨论时间复杂度是讨论最坏的时间复杂度,这样做的原因是:最坏请款下的时间复杂度是在任何输入实例的界限,这就保证了运行时间不会超过最坏的界限
平均时间复杂度和最坏时间复杂度是否一致,和算法有关系
常见算法的时间复杂度
| 排序法 | 平均时间 | 最差情形 | 稳定度 | 占用的额外空间 | 备注 |
|---|---|---|---|---|---|
| 冒泡 | O(n2) | O(n2) | 稳定 | O(1) | n小时较好 |
| 交换 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 选择 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 插入 | O(n2) | O(n2) | 稳定 | O(1) | 大部分已排序时较好 |
| 基数 | O(logRB) | O(logRB) | 稳定 | O(n) | B是真数(0-9) R是基数(个十百) |
| Shell | O(nlogn) | O(ns) 1<s<2 | 不稳定 | O(1) | s是所选分组 |
| 快速 | O(nlogn) | O(n2) | 不稳定 | O(nlogn) | n大时较好 |
| 归并 | O(nlogn) | O(nlogn) | 稳定 | O(1) | n大时较好 |
| 堆 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n大时较好 |
算法的空间复杂度
类似于时间复杂度的讨论,一个算法的空间复杂度定义为该算法所耗费的存储空间,它也是问题规模n的函数
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的度量。
有的算法需要占用的临时工作单元数与解决问题的规模n有关,它随着n的增大而增大,当n较大时,占用更多的存储单元,例如快排或者归并
在做算法分析时,主要讨论的是时间复杂度。从用户使用体验上来看,更看重的程序执行的速度。
一些缓存产品(redis,memcache)和算法(基数排序)本质就是用空间换时间
冒泡排序
冒泡排序概述
它的基本思路是
排序序列从前到后(下标从小到大),依次比较相邻元素的值,若发现逆序则交换,使值较大的元素主键从前意向后部
就像水底下的气泡一样逐渐上冒
冒泡排序需要执行多次,每一次都确定一个最大值
第一次确定所有数据的最大值,放到最后
第二次确定剩下数据的最大值,放到倒数第二个位置
第三次确定剩下数据的最大值,放到倒数第三个位置
...
第n次剩下了两个数据,确定这两个数据的较大值,放到第二个位置
排序完成
1、一共进行了数组大小-1次循环
2、每次排序的次数在主键减少
3、如果我们发现在某次排序中,没有发生一次交换,那么就可以提前结束冒泡排序
冒泡排序代码实现
package com.howling;
import java.util.Arrays;
public class BubbleSort {
public static void main(String[] args) {
int[] arr = {3, 9, -1, 10, -2};
//用来交换
int temp = 0;
//写为arr.length - 1,避免数组出界
for (int i = arr.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
//假如前面的数比后面的数大,那么交换
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
System.out.println("排序:" + Arrays.toString(arr));
}
}
}
排序:[3, -1, 9, -2, 10]
排序:[-1, 3, -2, 9, 10]
排序:[-1, -2, 3, 9, 10]
排序:[-2, -1, 3, 9, 10]
冒泡排序的适当优化
当我们发现某个排序中完全没有交换,那么冒泡提前结束
package com.howling;
import java.util.Arrays;
public class BubbleSort {
public static void main(String[] args) {
int[] arr = {3, 9, -1, 10, -2};
bubbleSort(arr);
}
/**
* 冒泡排序
*
* @param arr 需要冒泡排序的数组
*/
private static void bubbleSort(int[] arr) {
//用来交换
int temp = 0;
//定义一个表示变量,表示是否进行了交换
boolean flag = false;
//写为arr.length - 1,避免数组出界
for (int i = arr.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
//假如前面的数比后面的数大,那么交换
if (arr[j] > arr[j + 1]) {
flag = true;
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
//假如在一次循环中一次都没有进行交换,那么直接退出循环即可
if (!flag) {
break;
} else {
//重置flag,令其重新进行检测
flag = false;
}
System.out.println("排序:" + Arrays.toString(arr));
}
}
}
选择排序
选择排序概述
选择排序,也是一种简单的排序方法,它的基本思想是:
第一次从arr[0]-arr[n-1]中选取最小值,与arr[0]交换
第二次从arr[1]-arr[n-1]中选择最小值,与arr[1]交换
第三次从arr[2]-arr[n-1]中选择最小值,与arr[2]交换
....
第i次从arr[i-1]-arr[n-1]中选择最小值,与arr[i-1]交换
....
第n-1次从arr[n-2]-arr[n-1]中选择最小值,与arr[n-2]交换
共交换n-1次,得到一个按照排序码从小到大的有序序列
选择排序和冒泡排序其实差不多,很容易混淆
选择排序比较的次数没有改变,但是交换的次数少了
1、选择排序一共有数组大小-1次排序
2、每一轮排序,又是一次循环
3、先假定当前这个数是最小数,然后和后面的每个数进行比较,如果发现有比当前数更小的数,就重新确定最小数,并得到下标
4、当遍历到了数组的最后时,就得到本轮的最小数和下标
5、交换
选择排序代码实现
package com.howling;
import java.util.Arrays;
public class SortDemo {
public static void main(String[] args) {
//选择排序
int[] arr = {101, 34, 119, 1, 121, 82, 59};
selectSort(arr);
}
/**
* 选择排序
*
* @param arr 要进行排序的数组
*/
private static void selectSort(int[] arr) {
//minIndex:最小的数字的索引;min:最小的数字
int minIndex, min;
for (int i = 0; i < arr.length - 1; i++) {
//先假定当前的最小数字的索引为i
minIndex = i;
min = arr[minIndex];
//先假定当前的最小数字为arr[i]
for (int j = i; j < arr.length; j++) {
if (min > arr[j]) {
min = arr[j];
minIndex = j;
}
}
arr[minIndex] = arr[i];
arr[i] = min;
System.out.println("进行排序:" + Arrays.toString(arr));
}
}
}
进行排序:[1, 34, 119, 101, 121, 82, 59]
进行排序:[1, 34, 119, 101, 121, 82, 59]
进行排序:[1, 34, 59, 101, 121, 82, 119]
进行排序:[1, 34, 59, 82, 121, 101, 119]
进行排序:[1, 34, 59, 82, 101, 121, 119]
进行排序:[1, 34, 59, 82, 101, 119, 121]
插入排序
插入排序概述
插入排序的基本思想是:
把n个待排序的元素看为一个有序表和一个无序表
一开始:有序表只包含一个元素,无序表包含n-1个元素
后来:每次从无序表中取得第一个元素,将他的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表
比如,现在有一个数组R
int[] R = {17,3,25,14,20,9}
初始状态,将17看成一个有序表,剩下的看成一个无序表
第一次插入,取得无序表中的第一个值3,与有序表最后进行比较,发现3<17,则3向前挪一位,然后向前比较,没值了,就这样
第二次插入,取得无序表中的第一个值25,与无序表最后进行比较,发现25>17,那就这样
第三次插入,取得无序表中的第一个值14,与无序表最后进行比较,发现14<25,则向前移动一位,然后向前比较,发现14<17,则向前一位,然后向前比较,发现大于3,就这样
......
最后得到足后的数据
代码实现
package com.howling;
import java.util.Arrays;
public class SortDemo {
public static void main(String[] args) {
//插入排序
int[] arr = {101, 34, 119, 1, -1, 89};
insertionSort(arr);
}
/**
* 插入排序
*
* @param arr 要进行排序的数组
*/
private static void insertionSort(int[] arr) {
//定义要插入的数据
int indexValue;
//定义要进行比较的数据的下标
int index;
System.out.println("排序前:"+Arrays.toString(arr));
for (int i = 1; i < arr.length; i++) {
//初始化要插入的数据
indexValue = arr[i];
//这里就是规定要比较的数据的下标应该在有序表中,不能到达无序表
index = i - 1;
//这里规定下标,不能小于0,否则会造成数组越界
while (index >= 0) {
if (arr[index] > indexValue) {
arr[index + 1] = arr[index];
arr[index] = indexValue;
index--;
} else {
break;
}
}
System.out.println("排序:" + Arrays.toString(arr));
}
}
}
排序前:[101, 34, 119, 1, -1, 89]
排序:[34, 101, 119, 1, -1, 89]
排序:[34, 101, 119, 1, -1, 89]
排序:[1, 34, 101, 119, -1, 89]
排序:[-1, 1, 34, 101, 119, 89]
排序:[-1, 1, 34, 89, 101, 119]
插入排序存在的问题
当需要插入的数比较小时,后移的次数会明显增多,对效率有影响

希尔排序
希尔排序概述
希尔排序也是一种插入排序,是根据插入排序进行了一些简单的改进之后的一个更加高效的版本
由1959年,希尔提出的,所以称为希尔排序,也称为缩小增量排序。
插入排序的基本思想:
把记录按照下标的一定增量分组,对每组使用直接插入排序算法排序。
随着增量逐渐减少,每组包含的关键词越来越多,当增量减少至1时,整个文件恰好被分为一组,算法便终止
比如说,现在有一组数据:int[] arr = {8,9,1,7,2,3,5,4,6,0},长度为10
1、arr.length/2 = 5,也就是分为5组,步长也是5
根据步长,我们可以将他们分出来:
1组:arr[0],arr[0+5],也就是8和3
2组:arr[1],arr[1+5],也就是9和5
3组:arr[2],arr[2+5],也就是1和4
4组:arr[3],arr[3+5],也就是7和6
5组:arr[4],arr[4+5],也就是2和0
2、每一个组内进行数据的比较,然后进行排序,那么就变为了
int[] arr = {3,5,1,6,0,8,9,4,7,2}
3、缩小增量,原来的增量为5,现在进行5/2=2.5,但是我们取整数2,那么增量就为2,也就分为2组
1组:arr[0],arr[2],arr[4],arr[6],arr[8]。也就是3,1,0,9,7
2组:arr[1],arr[3],arr[5],arr[7],arr[9]。也就是5,6,8,4,2
4、组内进行排序,就变为了
int[] arr = {0,2,1,4,3,5,7,6,9,8};
5、缩小增量为2/2,也就是1,也就是分为了一组,那么在一组内进行了排序
希尔排序其实是插入排序的改进版,他最大的作用就是改善了较小值移动次数过多的情况
代码实现
希尔排序的交换法
/**
* 希尔排序交换法
*
* @param arr 要排序的数组
*/
private static void shellSortExchange(int[] arr) {
//因为每次每个组交换完成之后,步长都会/2,所以gap就是步长
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
/*
每次进行交换都是组内进行的交换
但是因为步长是一定的,所以我们只需要得到组内的一个值,就说明得到了全部的值
*/
for (int i = gap; i < arr.length; i++) {
/*
每次的交换肯定不可能只交换一次,比如说
- 假如arr[n]<arr[n+gap],那么不必进行交换
- 假如arr[n]>arr[n+gap]
1、arr[n],arr[n+gap]交换完了
2、接下来不应该去看arr[n+1]和arr[n+1+gap],应该去看arr[n]和arr[n-gap]是否是有序的
*/
for (int j = i - gap; j >= 0; j -= gap) {
if (arr[j] > arr[j + gap]) {
//两个数进行交换
arr[j] = arr[j] + arr[j + gap];
arr[j + gap] = arr[j] - arr[j + gap];
arr[j] = arr[j] - arr[j + gap];
} else {
break;
}
}
}
}
}
希尔排序的交换法
希尔排序的移动法
希尔排序的移位法真正整合了插入排序的优点,进行了移位的操作
/**
* 希尔排序移位法
*
* @param arr 要排序的数组
*/
private static void shellSortMove(int[] arr) {
//因为每次每个组交换完成之后,步长都会/2,所以gap就是步长
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < arr.length; i++) {
int j = i;
int temp = arr[j];
if (arr[j] < arr[j - gap]) {
while (j - gap >= 0 && temp < arr[j - gap]) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp;
}
}
}
}
希尔排序的插入法是比较难以理解的,我在这里做一下说明,使用希尔排序的位移法要从一开始看
1、arr[0]和arr[gap]无论谁大谁小,那么走一遍上面的路线,会发现两者会变为有序组
2、进行其他位置的排序....
3、arr[gapx2]和之前的位置比较,我们知道arr[0]和arr[gap]是有序的,所以无论arr[gapx2]插入到哪个位置,都不会扰乱这两者的顺序
4、....
5、arr[gapxn]和之前的位置比较,我们知道之前的等步长的所有位置上都是有序的,所以无论arr[gapxn]插入到哪里,都不会扰乱之前的顺序
快速排序
快速排序的概述
快速排序(Quicksort)是对冒泡排序的一种改进。
基本思想是:
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小。
然后再按此方法对这两部分数据分别进行快速排序。
整个排序过程可以递归进行,以此达到整个数据变成有序序列
比如说,现在有A,B,C,D,E五个数,我们以C为基准,把比C小的都放到C的左边,把比C大的都放到C的右边。
然后这样就分割成了两个区域X,Y。然后分别对两个区域内的数据重新进行排序分割,直到最后排序完成
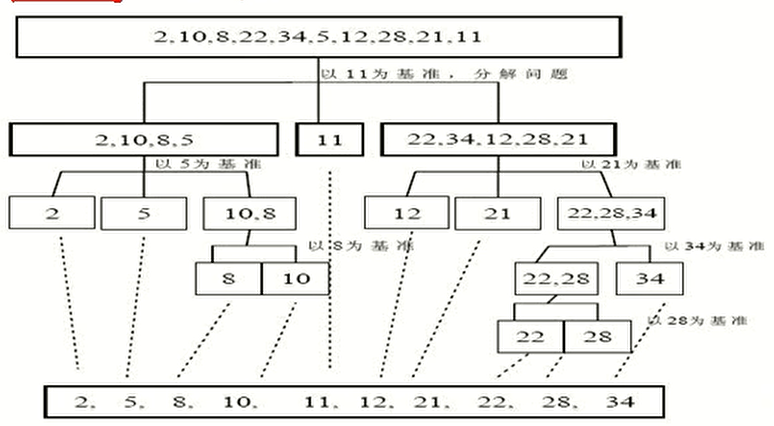
图中是以最后一个数为基准来进行分割的,但其实一什么为基准来分割并不重要,重要的是快速排序的思想
代码实现
/**
* 快速排序
*
* @param arr 要进行排序的数组
* @param left 数组0位置的下标,不会变
* @param right 数组length-1位置的下标,不会变
*/
private static void quickSort(int[] arr, int left, int right) {
//左下标
int l = left;
//右下标
int r = right;
//数组中间的值
int pivot = arr[(left + right) / 2];
//将左下标-右下标这段中,比中轴值大的放右边比中轴值小的放左边
while (l < r) {
/*
在中轴左边的值中,找到一个比中轴大的值
即使找不到等到了中轴也会停止
*/
while (arr[l] < pivot) {
l += 1;
}
/*
在中轴右边的值中,找到一个比中轴小的值
即使找不到到了中轴也会停止
*/
while (arr[r] > pivot) {
r -= 1;
}
/*
下面是交换的环节
交换的环节是有可能发生下面的环节:
- l和r都没有到达中轴,两边都找到了符合条件的数字,那么两者交换
- l和r都到达了中轴,那么说明了中轴左边全部小于中轴,右边全部大于中轴,那么直接跳出循环即可
- l到达中轴,但是r没有到达中轴,那么进行以下步骤:
1、 l和r进行交换,发现了l变为了比中轴小的数字,但是r直接变为了中轴
2、不慌,既然r变为了中轴,那么就让l向后移动一位,然后开启下一个while循环
3、根据我们的判断条件,r=pivot的时候保持不动,那么现在就是l进行扫描
4、l单独进行扫描,直到遇见一个大于等于pivot的数字,进入交换环节
- l没有到达中轴,但是r到达了中轴,那么进入交换步骤,具体情况类似上面的那个特殊情况
*/
if (l >= r) {
break;
}
arr[l] = arr[l] + arr[r];
arr[r] = arr[l] - arr[r];
arr[l] = arr[l] - arr[r];
/*
交换完成之后,发现arr[l]==pivot,那么r--
一定要让r--,否则极端情况(比如数组的数全部相等)的时候会死循环
*/
if (arr[l] == pivot) {
r -= 1;
}
if (arr[r] == pivot) {
l += 1;
}
}
//假如l==r,必须将两者错开,否则会造成栈溢出
if (l == r) {
l += 1;
r -= 1;
}
//中轴的左边进行递归,重新分组
if (left < r) {
quickSort(arr, left, r);
}
//中轴的右边进行递归,重新分组
if (right > l) {
quickSort(arr, l, right);
}
}
public static void main(String[] args) {
int[] arr = {-9, 78, 0, 23, -567, 70, -1, 900, 4561};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
归并排序
归并排序概述
归并排序,是分支策略思想进行实现的一种排序算法。
分治策略的意思是:
1、分:将大的问题分为小的问题,分解完成之后。没有什么实质性的动作
2、治:将分出来的结果形成答案,合并到一起
我们后面还有一个分治算法,也是分支策略的一种实现。
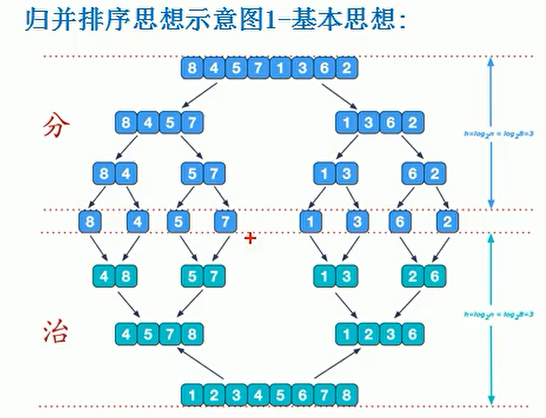
我们可以看到,分治中的分为了单独的数据,然而治是合并了7次。
数据一共有8个,合并了七次,这就是效率十分高明的一种合并方式。
这么算来,即使有八十万,八百万,也会在它之上减一次,这是效率十分高的一种方式。它是线性增长,如果是冒泡,早就已经凉了。
我们来讲一下它是怎么进行合并的,我们以最后一次的合并为例子来进行讲解
也就是上图中的[4 , 5 , 7 , 8]和[1 , 2 , 3 , 6]来作为例子来进行讲解
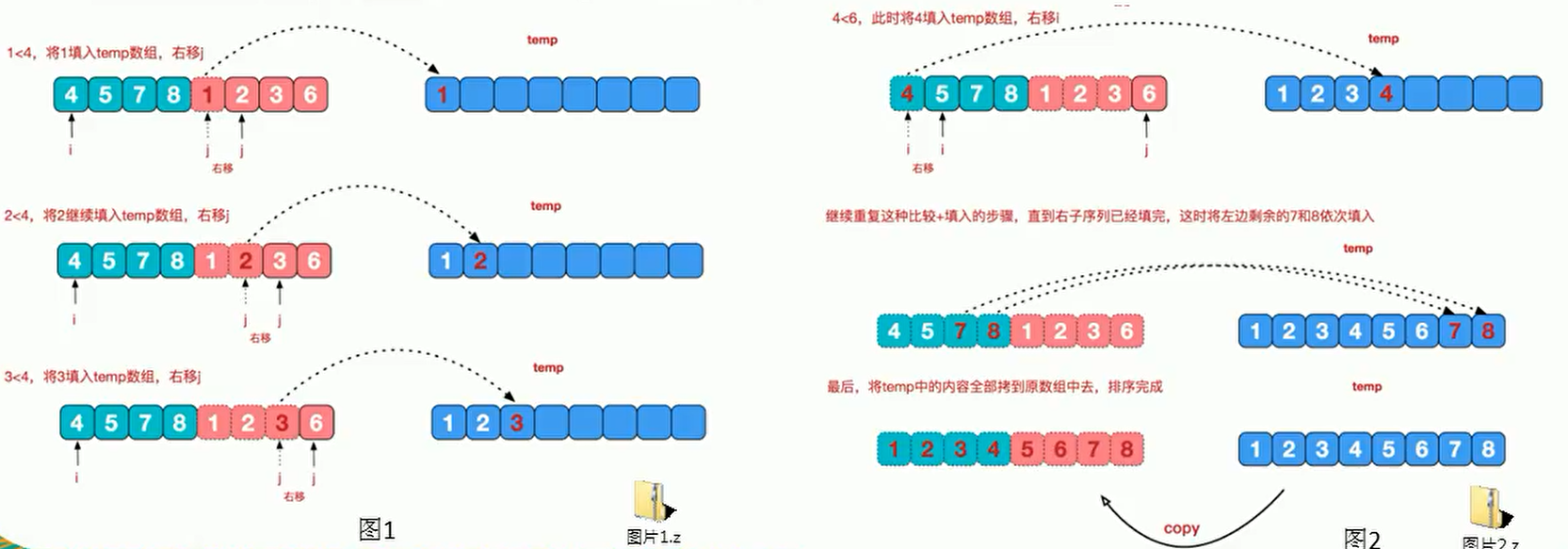
1、我们首先定义两个指针: i 和 j ,其中 i 指向左边的分类, j 指向右边的分类。然后定义一个临时数组 temp 用于存放数据
2、 i 和 j 指向的数据进行比较,假如 i 比较小,那么将 i 指向的数据放到 temp 中,然后i+1。反之亦然
3、重复以上步骤,直到排序完成
4、假如出现 i 部分已经完成, j 部分未完成,只需要将 j 部分全部加入 temp 中即可,因为i和j两个单独的部分都是顺序的。
代码实现
/**
* 归并排序中的分开部分+合并部分
*
* @param arr 原数组
* @param left 数组左
* @param right 数组右
* @param temp 临时数组
*/
private static void mergeSortPoints(int[] arr, int left, int right, int[] temp) {
//分
if (left < right) {
//中间的索引
int mid = (right + left) / 2;
//向左递归进行分解
mergeSortPoints(arr, left, mid, temp);
//向右递归进行分解
mergeSortPoints(arr, mid + 1, right, temp);
//治,每次进行一次分解都要进行一次合并
mergeSortTreatment(arr, left, mid, right, temp);
}
}
/**
* 归并排序中的合并部分:治
*
* @param arr 要进行排序的原数组
* @param left 数组的最左边
* @param mid 左指针和右指针的分界线,在这里我们定义为左半部分的最后一个元素
* @param right 数组的最右边
* @param temp 临时数组
*/
private static void mergeSortTreatment(int[] arr, int left, int mid, int right, int[] temp) {
//初始化左边部分的初始化索引
int i = left;
//初始化右边部分的初始化索引
int j = mid + 1;
//指向temp数组的当前索引
int t = 0;
/*
1、先把左右两边的有序数据填充到temp数组中,直到左右两边的有序序列有一边处理完毕即可
*/
while (i <= mid && j <= right) {
//当左边的元素<右边的元素,那么将左边的元素拷贝到temp数组中,然后将t和i向后移动
if (arr[i] < arr[j]) {
temp[t] = arr[i];
t++;
i++;
}
//反之亦然
else {
temp[t] = arr[j];
t++;
j++;
}
}
/*
2、将有剩余的一边的数据依次,全部填充到temp中
假如左边的有序序列还有剩余的元素,那么全部填充到temp中
*/
while (i <= mid) {
temp[t] = arr[i];
t++;
i++;
}
//在j中也是一样的道理
while (j <= right) {
temp[t] = arr[j];
t++;
j++;
}
/*
3、将temp数组的元素全部重新拷贝到arr
注意,并不是每一次都要拷贝arr.length()个数,比如我们在分支算法中的分中,原数组:
8 4 5 7 1 3 6 2
分成了
8 4 5 7 1 3 6 2
我们在第一次治的时候,是这样的:
48 57 13 26
所以拷贝的时候是两个两个地拷贝,而不是拷贝8个
*/
t = 0;
int tempLeft = left;
/*
第一次合并时,tempLeft=0,right=1,看前面的例子是8和4进行合并,也就是我们左和右的合并
第二次合并时,tempLeft=2,right=3,在这里就是5和7的合并,也就是我们左和右的合并
第三次合并时,tempLeft=0,right=3,这是因为从索引0-索引3中,是我们定义的左边部分和右边部分的合并
然后第四次,第五次,第六次就是我们的1和3进行合并。2和6进行合并。13和26的合并
最后一次就是4578和1236的合并
*/
while (tempLeft <= right) {
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
System.out.println();
}
基数排序
基数排序概述
基数排序介绍
1、基数排序(radix sort)是属于分配式排序(distribution sort),又称桶子法(bucket sort 或者 bin sort)。
顾名思义,它是通过键值的各个位的值,将要排序的元素分配到某一些桶中,达到排序的作用
2、基数排序是属于稳定性的排序,基数排序法是效率最高的稳定性排序法
稳定性排序的意思是:我现在有四个数字,3,1,41,1
排序之后是:1,1,3,41
但是1的顺序还是原来的顺序,第一个1就是排序之后的第一个1,第二个1就是排序之后的第二个1
相同元素的顺序是不变的
3、基数排序是桶排序的扩展,也就是说,学完了基数排序之后,学习桶排序也是十分简单的
基数排序的基本思想
1、将所有待比较的数值统一为同样的数位长度,数位较短的数字前面补零。
2、从最低为开始,依次进行一次排序
3、这样从最低位排序一直到最高位排序完成之后,数列就变为了一个有序序列
它的图文表现是这样的:
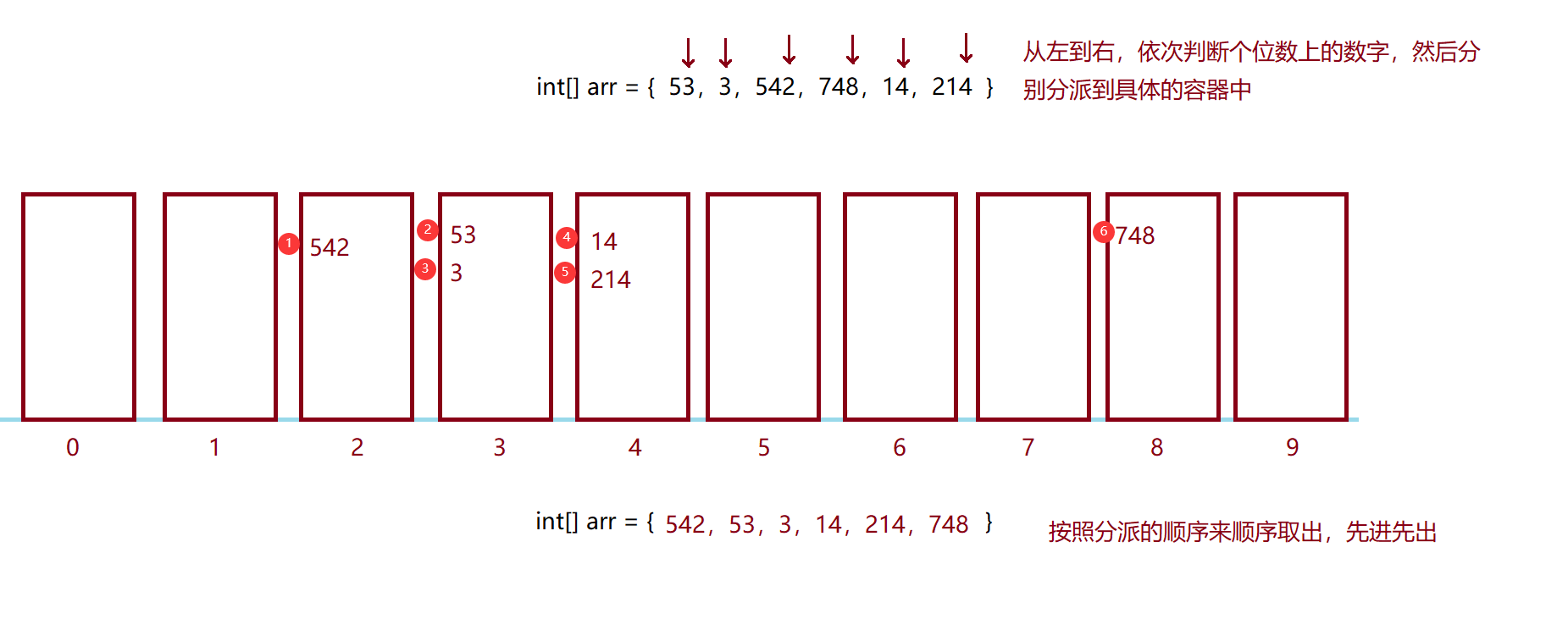
我们的原数组是这样的:
int[] arr = {53 , 3 , 542 , 748 , 14 , 214}第一轮:比较个位数
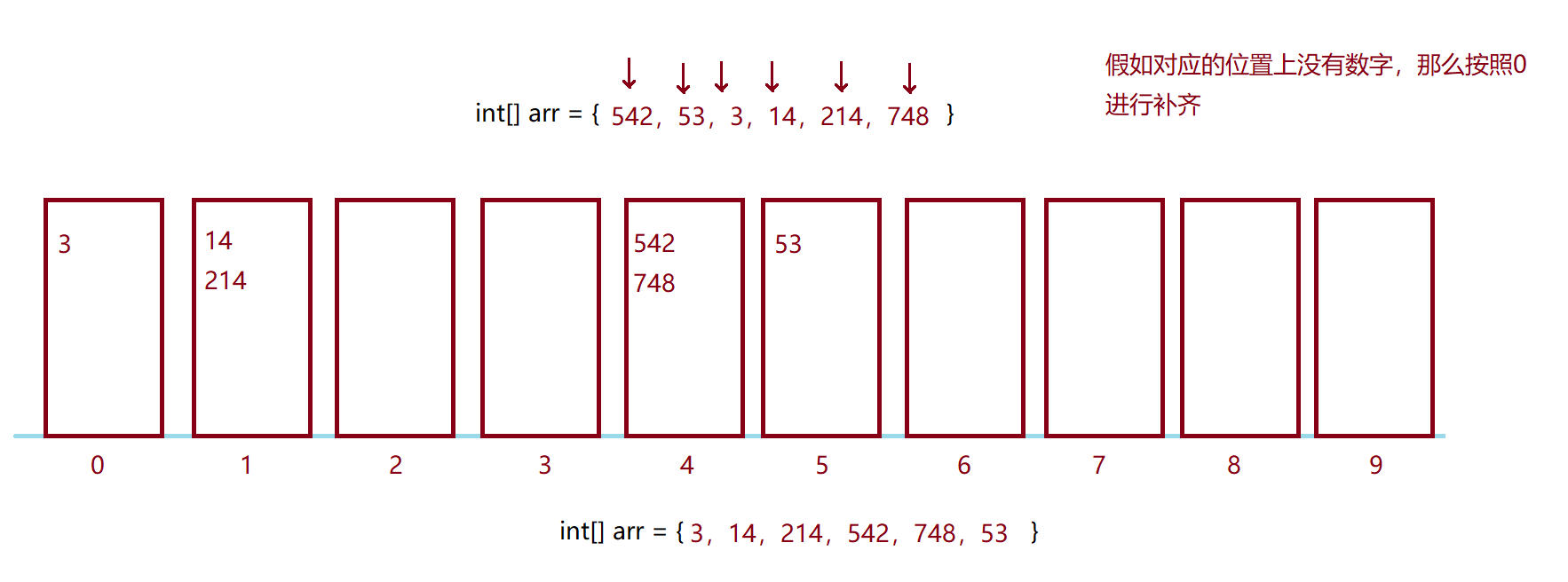
第二轮:比较十位数
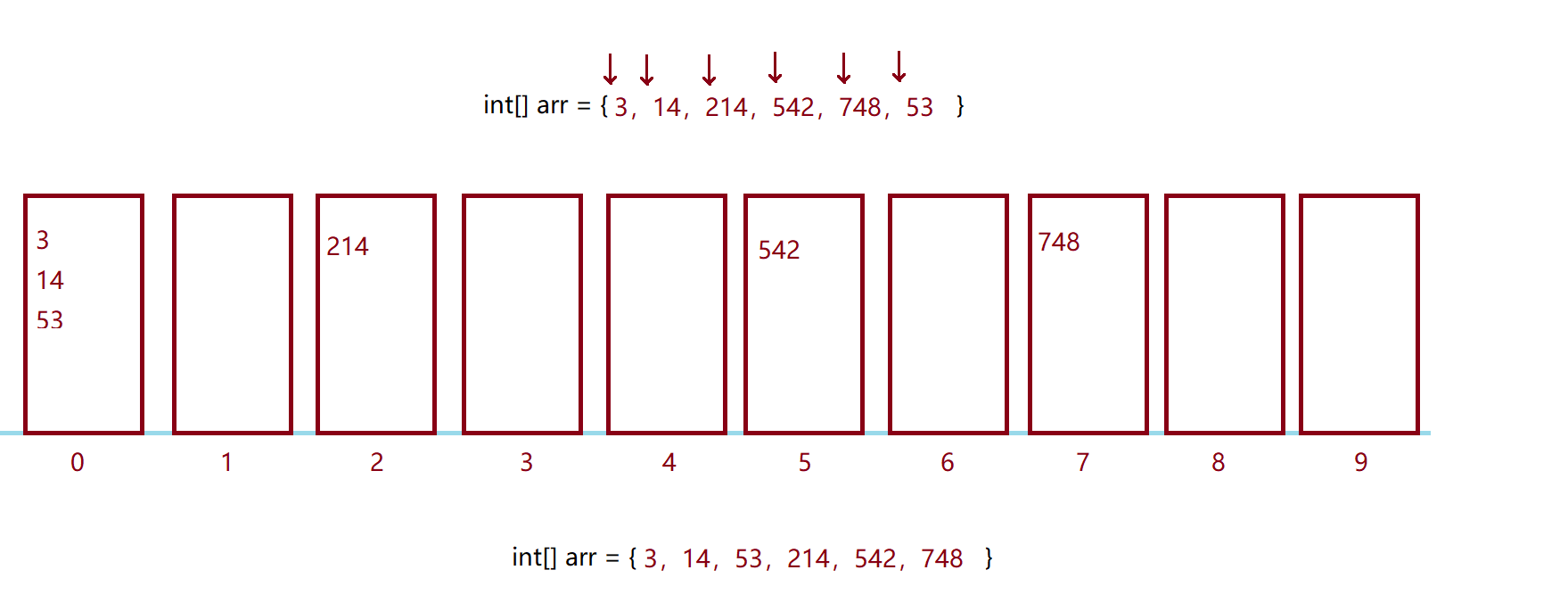
第三轮:比较百位数
因为没有更高位了,所以没有第四轮
代码实现
/**
* 基数排序
*
* @param arr 要排序的数组
*/
private static void redixSort(int[] arr) {
/*
1、定义一个数组桶,桶的个数为10,每个桶的容量为arr.length
为了保证数据不溢出,只能采用空间换时间的方式
基数排序,是空间换时间的经典算法
*/
int[][] bucket = new int[10][arr.length];
/*
2、桶中有效数据的个数
为了保证我们知道每一个桶中应该存在几个数据
所以在每一个数组桶中,应该有一个指针指向桶的最后添加的数据
以此来判断数组桶的数据量个数
比如bucket[0]的值,就是第一个桶中放入的有效数据的个数
*/
int[] bucketElementCounts = new int[10];
/*
3、根据最长数字获得长度
*/
//首先定义一个最大值,然后通过遍历查找到最大的值,最后只需要判断最大值的长度即可
final int[] max = {0};
Arrays.stream(arr).forEach(e -> {
max[0] = max[0] > e ? max[0] : e;
});
//获得最大数值的长度
int maxLength = (max[0] + "").length();
/*
4、
取得个位放到数组桶中,然后取出元素到数组中
取得十位放到数组桶中,然后取出元素到数组中
......
*/
for (int length = 0; length < maxLength; length++) {
//求10的length次方
double pow = Math.pow(10, length);
//获得对应的位数,然后把元素放到对应的数组桶中
for (int e : arr) {
int index = (int) (e / pow % 10);
bucket[index][bucketElementCounts[index]] = e;
bucketElementCounts[index]++;
}
//数组下标索引
int j = 0;
//取出数组桶中的元素,放到数组中
for (int b = 0; b < bucket.length; b++) {
for (int index = 0; index < bucketElementCounts[b]; index++) {
arr[j] = bucket[b][index];
j++;
}
//将指针重置
bucketElementCounts[b] = 0;
}
}
}
注意,基数排序会耗费额外的内存空间,注意不要让内存溢出
而且,假如为负数,我们就不要使用基数排序,因为会进行数组越界,除非进行代码的改动
八万个数据下,各个排序的时间
1、首先我们需要一个工具
public static void main(String[] args) {
int[] arr = new int[80000];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * 80000);
}
long start = System.currentTimeMillis();
// 排序的方法写在这
long end = System.currentTimeMillis();
System.out.println((end - start) + "毫秒");
}
经过我们的测试:
- 冒泡排序:10~11秒左右
- 选择排序:4000~4500毫秒左右
- 插入排序:1800~1900毫秒左右
- 希尔排序交换法:49毫秒,八百万的数组容量下消耗3874毫秒
- 希尔排序移动法:31毫秒,八百万的数组容量下消耗2716毫秒
- 基数排序法:132毫秒,八百万的数组容量下小号2091毫秒
- 快速排序法:30毫秒,八百万的数组容量下消耗1705毫秒
- 归并排序法:22毫秒,八百万的数组容量下消耗1819毫秒