逻辑回归
逻辑回归是用于解决离散型的输出结果的问题（分类问题）。文本分类就是一个典型的分类问题。
在描述线性回归数学模型之前，先约定好一些表达形式：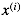 
代表输入数据 （features），
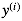代表输出数据（分类标签），
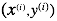代表一组训练数据（training example） ，m代表训练数据的个数，n代表特征数量。
1 逻辑回归函数表达
对于逻辑回归分类问题，y的输出等于 0 或者 1。逻辑回归函数式的输出范围是: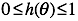
，以0.5作为临界值（Threshhold），y的取值如下：
如果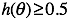
，y = 1
如果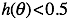
， y = 0
函数式表达
逻辑回归的函数表达如下：
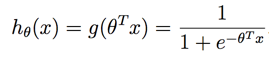
其中
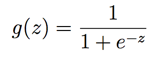
逻辑回归的损失函数是它的极大似然函数
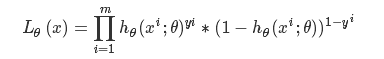
逻辑回归的整个代价函数表示如下：
2 梯度下降算法
有了代价函数，接下来对于逻辑回归需要解决的事情往就是希望能够找到一组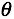
，能够最小化
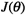，即
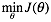，梯度下降算法基本方式如下：
1) 随机选择一组；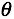
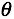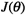2) 不断的变化，让变小；
j=0,1,...n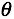，是所有n+1个值同时进行变化。α 是代表学习速率。是损失函数对的偏导数。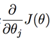 
3) 直到寻找到最小值。
所以关键是推导出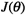对于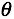j的偏导数如下： 
逻辑回归的多分类：
N分类也就是训练N个二分类。对于第j个分类器，任务就是得出一个样本属于j类和其他类的概率 hθ(i)(x) 。
求得所有二分类后j（j = 1,2,3…N），那么这个样本属于的类J当:
hθ(J)(x) =