2017-2018-1 20155329 《信息安全系统设计基础》第13周学习总结

2017-2018-1 20155329 《信息安全系统设计基础》第13周学习总结

第五章重点内容

优化程序性能

1. 与机器有关
2. 与机器无关

CPE表示程序的性能

用每元素的周期数（cycles per element，CPE）来度量程序的循环性能，CPE越小表示性能越好。

第五章内容

与机器无关

• 1-6节讲的就是如何“大众化”地优化代码，也就是说不依赖于目标机器的任何特征。

• 循环展开的技术（loop unrolling）

循环展开就是通过在每次迭代中执行更多的数据操作来减小循环开销的影响。其基本思想是设法把操作对象线性化，并且在一次迭代中访问线性数据中的一小组而非单独的某个。这样得到的程序将执行更少的迭代次数，于是循环开销就被有效地降低了。

• 将命令开关设置为“-O2”
• 代码移动（code motion）

如果某个函数的计算结果是个常数，那么我们就不应该把他放在循环里面，而可以将计算机移动到代码前面的，不会被多次求值的部分。

• 减少调用过程

这种方法存在一个缺点，就是它是以损害一些程序的模块性为代价的。所以修改这些代码，需要添加一些对所做改变的说明文档。

• 消除不必要的存储器的引用。在循环中不停地对指针所指向的变量赋值的时候，我们可以用一个中间变量代替指针，以增加速度。
• 转换到指针代码。其实指针和数组代码的相对性会随着机器不同而不同。而编译器对数组代码应用非常高级的优化，而对指针代码只引用最小限度的优化。所以数组代码更可取
• 寄存器溢出。循环并行性的收益是受到处理器硬件资源特别是寄存器数量的限制的。当并行度导致寄存器数量不足时，只能将临时值存放在堆栈中。一旦出现这种情况，性能就会急剧下降。一个通用的原则是无论何时当程序显示出在某个频繁使用的内循环中存在寄存器溢出的迹象时，都应该重写代码，减少循环中涉及的局部变量。

与机器有关

• 5.7理解现代处理器（感觉一知半解，模模糊糊的）
• 5.9 提高并行性

选择第五章原因

• 原因1：写代码的时候我总想在力所能及的范围内将代码写的更好一些，精简一些！

第五章习题

• 5.13

A

B:
由浮点数加法的延迟，CPE的下界应该是3。

C:
由整数加法的延迟，CPE的下界应该是1.

D:
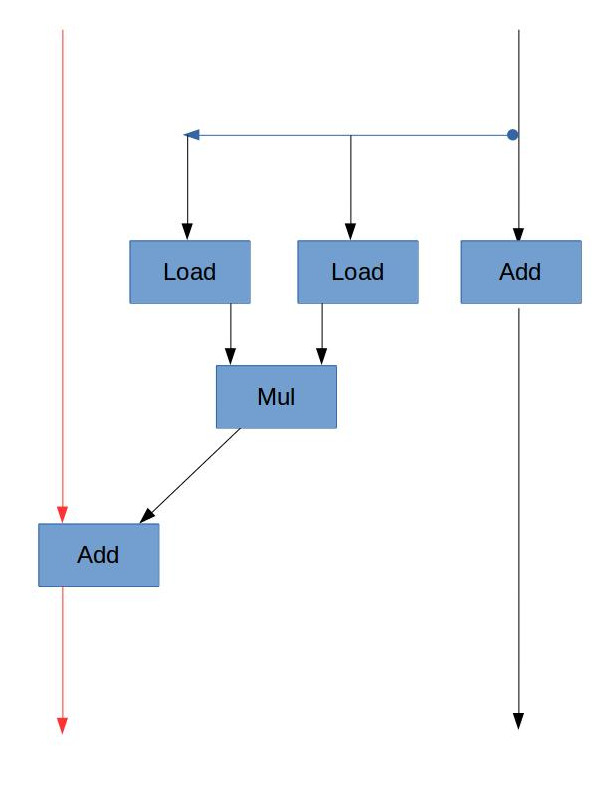
由A中的数据流图，虽然浮点数乘法需要5个周期，但是它没有“数据依赖”，也就是说，每次循环时的乘法不需要依赖上一次乘法的结果，可以各自独立进行。但是加法是依赖于上一次的结果的（sum = sum + 乘法结果），所以该循环的“关键路径”是加法这条链。而浮点数加法的延迟为3个周期，所以CPE为3.00。

• 5.14

A: 由5.13中分析的，关键路径是一个加法，而整数加法的延迟为1个周期，所以CPE的下界为1。

B: “6 * 1 loop unrolling”只减少了循环的次数（所以整数的CPE下降了，书上把这个称为“overhead”），并没有减少内存读写的次数和流水线的发生，所以浮点数运算还是不能突破“关键路径”的CPE下界。

• 5.15

/* 6 * 6 loop unrolling */
/*省略*/
data_t sum1 = (data_t) 0;
data_t sum2 = (data_t) 0;
data_t sum3 = (data_t) 0;
data_t sum4 = (data_t) 0;
data_t sum5 = (data_t) 0;

for(i = 0; i < length; i += 6)
{
  sum1 = sum1 + udata[i] * vdata[i];    /* 相互独立，可以流水线 */
  sum2 = sum2 + udata[i+1] * vdata[i+1];
  sum3 = sum3 + udata[i+2] * vdata[i+2];
  sum4 = sum4 + udata[i+3] * vdata[i+3];
  sum5 = sum5 + udata[i+4] * vdata[i+4];
  sum6 = sum6 + udata[i+5] * vdata[i+5];
}

for(; i < length; ++i)
{
  sum1 = sum1 + udata[i] * vdata[i];
}

*dest = sum1 + sum2 + sum3 + sum4 + sum5 + sum6;

-虽然此时也可以流水线，但是浮点数加法的单元的Issue time为1个周期，而Capacity也为1，所以最多每个时钟周期完成I/C = 1个加法操作，即此时CPE的下界为1。

• 5.16

/* 6 * 1a loop unrolling */
/*省略*/
data_t sum1 = (data_t) 0;
data_t sum2 = (data_t) 0;
data_t sum3 = (data_t) 0;
data_t sum4 = (data_t) 0;
data_t sum5 = (data_t) 0;

for(i = 0; i < length; i += 6)
{
  sum = sum + (udata[i] * vdata[i] + udata[i+1] * vdata[i+1] + udata[i+2] * vdata[i+2] + udata[i+3] * vdata[i+3] + udata[i+4] * vdata[i+4] + udata[i+5] * vdata[i+5]);
}

for(; i < length; ++i)
{
  sum = sum + udata[i] * vdata[i];
}

*dest = sum;

• 5.17

#include <limits.h>
#define K sizeof(unsigned long)
void *word_memset(void *s, int c, size_t n)
{
  if (n < K)
  {
    size_t cnt = 0;
    unsigned char *schar = s;
    while (cnt < n)
    {
        *schar++ = (unsigned char)c;
        cnt++;
    }
  }
  else
  {
      unsigned long word = 0;
      for (int i = 0; i < K; ++i)
      {
        word <<= K*CHAR_BIT;
        word += (unsigned char)c;
      }

      size_t cnt = 0;
      unsigned long *slong = s;
      while (cnt < n)
      {
        *slong++ = word;
        cnt += K;
      }
      
      unsigned char *schar = slong;
      while (cnt < n)
      {
        *schar++ = (unsigned char)c;
        cnt++;
      }
  }
  return s;
}

• ** 5.18**

书上给出的K >= L*C P371），其中L是latency，C是capacity，由于浮点数乘法分别对应5和2，所以这里的K选择为10。

K大的时候很可能会碰到寄存器不够的情况，不得不使用栈来保存局部变量（运行的时候会加载到高速缓存），会有一些性能上的牺牲。

double faster_poly(double a[], double x, long degree)
{
    long i;
    double result1 = a[0];
    double result2 = 0;
    double result3 = 0;
    double result4 = 0;
    double result5 = 0;
    double result6 = 0;
    double result7 = 0;
    double result8 = 0;
    double result9 = 0;
    double result10 = 0;

    double xpwr1 = x;
    double xpwr2 = xpwr1 * x;
    double xpwr3 = xpwr2 * x;
    double xpwr4 = xpwr3 * x;
    double xpwr5 = xpwr4 * x;
    double xpwr6 = xpwr5 * x;
    double xpwr7 = xpwr6 * x;
    double xpwr8 = xpwr7 * x;
    double xpwr9 = xpwr8 * x;
    double xpwr10 = xpwr9 * x;
    double x10 = xpwr10;

    for (i = 1; (i+9) <= degree; i += 10)
    {
        result1 += a[i] * xpwr1;
        result2 += a[i+1] * xpwr2;
        result3 += a[i+2] * xpwr3;
        result4 += a[i+3] * xpwr4;
        result5 += a[i+4] * xpwr5;
        result6 += a[i+5] * xpwr6;
        result7 += a[i+6] * xpwr7;
        result8 += a[i+7] * xpwr8;
        result9 += a[i+8] * xpwr9;
        result10 += a[i+9] * xpwr10;

        xpwr1 *= x10;
        xpwr2 *= x10;
        xpwr3 *= x10;
        xpwr4 *= x10;
        xpwr5 *= x10;
        xpwr6 *= x10;
        xpwr7 *= x10;
        xpwr8 *= x10;
        xpwr9 *= x10;
        xpwr10 *= x10;
    }
    for (; i <= degree; ++i)
    {
        result1 += a[i] * xpwr1;
        xpwr1 *= x;
    }
    
    result1 += result2;
    result1 += result3;
    result1 += result4;
    result1 += result5;
    result1 += result6;
    result1 += result7;
    result1 += result8;
    result1 += result9;
    result1 += result10;
    return result1;
}

• 5.19

瓶颈在于val=val+a[i] （书上还加了last_val ，一个意思）这一句，加法数据依赖，由书上给出的K >= L*C

（第P371)，其中L是latency，C是capacity，由于浮点数加法分别对应3和1，所以这里选择3*1a。

void faster_psum1a(float a[], float p[], long n)
{
    long i;
    float val = 0;
    for (i = 0; (i+2) < n; i += 3)
    {
        float tmp1 = a[i];
        float tmp2 = tmp1 + a[i+1];
        float tmp3 = tmp2 + a[i+2];
        
        p[i] = var + tmp1;
        p[i+1] = var + tmp2;
        p[i+2] = var = var + tmp3;
    }
    for (; i < n; ++i)
    {
        var += a[i];
        p[i] = var;
    }
}

第五章的一点思考（问题）

• 对于5.5和5.6两节中，若进行多项式计算
  时。用函数poly和horner相比，用书本上知识解释的话；horner法，通过反复提出幂，来减少乘法的次数，按照道理说，既然polyh函数比poly函数减少了乘法的次数，那应该比poly快才对。但是事实是相反的这是为什么呢？

疑问解答参考博客

第五章知识总结参考