线性回归模型

1、回归（regression）与  分类（Classification）区别，前者处理的是连续型数值变量。后者处理的是类别变量。

2、回归分析：建立方程模拟2个或多个变量之间关联关系。

3、简单线性回归：y=b1*x+b0

                                                                  

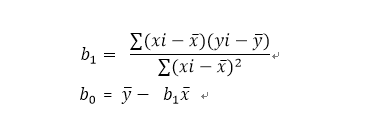
1) 参数b1,b0可以由如上公式计算出来，xi,yi为样本中各点。numpy实现简单线性回归方程。

# y = b1*x+b0
import numpy as np

def fitSLR(x,y):
	n = len(x)
	fenzi = 0
	fenmu = 0
	for i in range(0,n):
		fenzi = fenzi + (x[i]- np.mean(x))*(y[i]- np.mean(y))
		fenmu = fenmu + (x[i]- np.mean(x))**2
	print(fenzi)
	print(fenmu)
	b1 = fenzi/float(fenmu)
	b0 = np.mean(y)- b1*np.mean(x) 
	print(“b0:”,b0,"b1:",b1)
	return b0,b1

def predict(x,b0,b1):
	return b0+b1*x

x = [1,3,2,1,3]
y = [14,24,18,17,27]

b0,b1 = fitSLR(x,y)
x_test = 6
y_test = predict(x_test,b0,b1)

print("y_test", y_test)

　得出：b0: 10.0   b1: 5.0

2）调用statsmodels统计建模模块中的ols函数

import statsmodels.api as sm

import statsmodels.api as sm 
import pandas as pd
import numpy as np 

x = [1,3,2,1,3]
y = [14,24,18,17,27]
data = np.vstack((x,y))
dat = pd.DataFrame(data.T,columns = ['x','y'])
fit = sm.formula.ols('y ~ x',data = dat).fit()
print(fit.params)

 结果为：

　　

3) sklearn子模块linear_model中的LinearRegression方法

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

x = np.array([1,3,2,1,3])
y = np.array([14,24,18,17,27])


model = LinearRegression(fit_intercept = True)
model.fit(x[:,np.newaxis], y)

xfit = np.linspace(0,10,1000)
yfit = model.predict(xfit[:,np.newaxis])

plt.scatter(x,y)
plt.plot(xfit,yfit)
plt.show()

print("Model slope:  " , model.coef_[0])
print("Model intercept:  " , model.intercept_)

　　此方法注意引入的x、y须为array形式

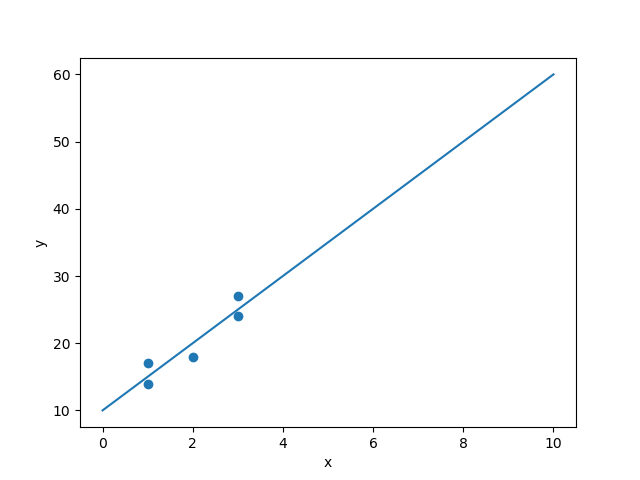
Model slope: 4.999999999999998
Model intercept: 10.000000000000004

4、多元线性回归

 python模块中有2种方式均可构建多元线性回归模型，一种是简单线性回归中sklearn子模块linear_model，还可以利用statsmodels统计建模模块中的ols函数进行构建。

1）statsmodels模块(ols函数)

from sklearn import model_selection # 便于交叉验证，可将模块分解成一定数量训练集和测试集
import statsmodels.api as sm
import pandas as pd 
import numpy as np 
import matplotlib.pyplot as plt

Profit = pd.read_excel(r'Predict to Profit.xlsx')
Profit.head()

　　

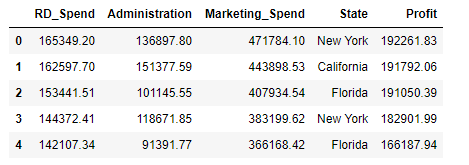
 数据集中State变量为非连续性变量，需要进行转化成哑变量。

# 对离散型变量State，需进行量化处理，（哑变量）
train, test = model_selection.train_test_split(Profit, test_size =0.2, random_state = 1234)
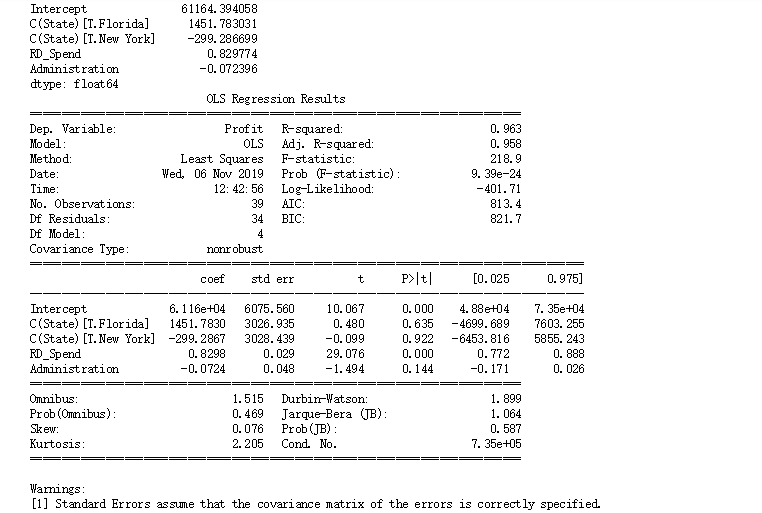
model = sm.formula.ols('Profit~RD_Spend+Administration+Administration+C(State)',data = train).fit() 

# 回归系数params
model.params

# 查看模型总的情况
model.summary()

　结果中State值的回归系数只出现2个，原因是建模时State的3个值，另外一个值State.California被用作了对照组。

 

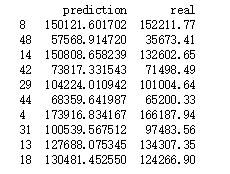
模型预测后结果：

2）sklearn子模块linear_model。

引入模块，生成哑变量

from sklearn import preprocessing
from sklearn import model_selection 
from sklearn.linear_model import LinearRegression
import pandas as pd
import numpy as np

Profit = pd.read_excel(r'Predict to Profit.xlsx')

dummy_Profit = pd.get_dummies(Profit['State'],prefix = 'State')  # 转化哑变量
Profit_d = Profit.join(dummy_Profit).drop('State',axis =1)
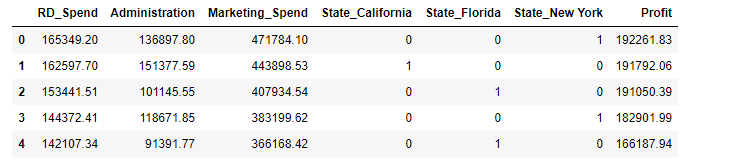
columns = ['RD_Spend','Administration','Marketing_Spend','State_California','State_Florida','State_New York','Profit']
Profit_d = Profit_d[columns]

　转化后数据集前5行：

 模型训练及预测：

train,test = model_selection.train_test_split(Profit_d,test_size=0.2,random_state=1234)
model = LinearRegression(fit_intercept = True)
model.fit(train.iloc[:,:-1],train.iloc[:,-1])

print(model.intercept_)
print(model.coef_)

test_X = test.drop(labels = 'Profit',axis =1)
pred = model.predict(test_X)
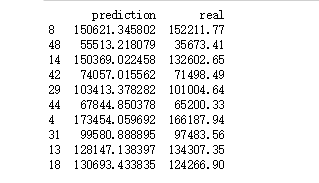
print(pd.DataFrame({'prediction':pred , 'real':test.Profit}))

　预测结果：　

　

 以上2种方式比较，使用statsmodels中ols函数构建线性回归模型时，若数据集中存在离散变量，需构建哑变量，构建方式将其变成分类变量：C(变量)的形式处理。而linear_model构建线性模型时，数据集中离散变量通过引入preprocessing模块，通过get_dummies()函数处理。

　　

 3）对于第一种ols函数方法哑变量中对照组值是系统自动确定的，如需要指定对照组。可以先采用pandas中get_dummies()函数生成哑变量，在删除掉对照组对应的哑变量值。

# 选定State中New York作为对照组
dummies = pd.get_dummies(Profit.State,prefix = 'State')
Profit_New = pd.concat([Profit,dummies],axis=1)
Profit_New.drop(labels = ['State','State_New York'],axis =1,inplace = True)

train , test = model_selection.train_test_split(Profit_New,test_size = 0.2,random_state=1234)
model = sm.formula.ols('Profit~RD_Spend+Administration+Marketing_Spend+State_California+State_Florida',data = train).fit()
model.params　　

　 以New York作为对照组的各偏回归系数情况如下：

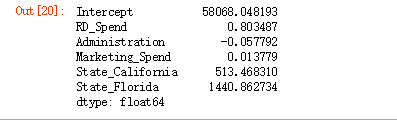
得到回归方程：Profit =  58068.048193 + 0.803487RD_Spend  - 0.057792Administration + 0.013779Marketing_Spend + 513.468310State_California + 1440.862734State_Florida  ，  其他变量不变的情况下，RD_Spend每增加1美元，Profit 增加0.803487美元，以new york 为基准，如果在State_Florida销售产品，利润会增加1440.862734。 

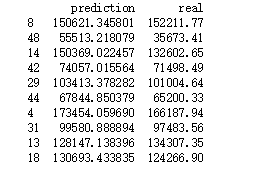
 生成预测值：

test_X = test.drop('Profit',axis=1)
pred = model.predict(test_X)
print(pd.DataFrame({"prediction":pred,"real":test.Profit}))

　对比test值：