Codeforces Round #344 (Div. 2) A

A. Interview

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Blake is a CEO of a large company called "Blake Technologies". He loves his company very much and he thinks that his company should be the best. That is why every candidate needs to pass through the interview that consists of the following problem.

We define function f(x, l, r) as a bitwise OR of integers x_l, x_l + 1, ..., x_r, where x_i is the i-th element of the array x. You are given two arrays a and b of length n. You need to determine the maximum value of sum f(a, l, r) + f(b, l, r) among all possible 1 ≤ l ≤ r ≤ n.

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 1000) — the length of the arrays.

The second line contains n integers a_i (0 ≤ a_i ≤ 10⁹).

The third line contains n integers b_i (0 ≤ b_i ≤ 10⁹).

Output

Print a single integer — the maximum value of sum f(a, l, r) + f(b, l, r) among all possible 1 ≤ l ≤ r ≤ n.

Examples

Input

5
1 2 4 3 2
2 3 3 12 1

Output

22

Input

10
13 2 7 11 8 4 9 8 5 1
5 7 18 9 2 3 0 11 8 6

Output

46

Note

Bitwise OR of two non-negative integers a and b is the number c = a OR b, such that each of its digits in binary notation is 1 if and only if at least one of a or b have 1 in the corresponding position in binary notation.

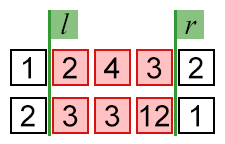
In the first sample, one of the optimal answers is l = 2 and r = 4, because f(a, 2, 4) + f(b, 2, 4) = (2 OR 4 OR 3) + (3 OR 3 OR 12) = 7 + 15 = 22. Other ways to get maximum value is to choose l = 1 and r = 4, l = 1 and r = 5, l = 2 and r = 4, l = 2 and r = 5, l = 3 and r = 4, or l = 3 and r = 5.

In the second sample, the maximum value is obtained for l = 1 and r = 9.

题解： max（f(a,l,r)+f((b,l,r)）  f() 为求 l-->r的按位或的值

马上codeforces  上分

#include<bits/stdc++.h>
using namespace  std;
int a[1002][1002];
int b[1002][1002];
int exm1[1002],exm2[1002];
int main()
{
    int n;
    int sum1=0,sum2=0,maxn=0;;
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&exm1[i]);
    }
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&exm2[i]);
    }
    for(int i=1; i<=n; i++)
    {
        sum1=exm1[i];
        a[i][i]=sum1;
        for(int j=i+1; j<=n; j++)
            {
                a[i][j]=sum1|exm1[j];
                sum1=a[i][j];
            }
    }
    for(int i=1; i<=n; i++)
    {
        sum2=exm2[i];
        b[i][i]=sum2;
        if(b[i][i]+a[i][i]>maxn)
                    maxn=b[i][i]+a[i][i];
        for(int j=i+1; j<=n; j++)
           {
                b[i][j]=sum2|exm2[j];
                sum2=b[i][j];
                if(b[i][j]+a[i][j]>maxn)
                    maxn=b[i][j]+a[i][j];
           }
    }
    printf("%d
",maxn);
    return 0;
}