Codeforces Round #324 (Div. 2) D

D. Dima and Lisa

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Dima loves representing an odd number as the sum of multiple primes, and Lisa loves it when there are at most three primes. Help them to represent the given number as the sum of at most than three primes.

More formally, you are given an odd numer n. Find a set of numbers p_i (1 ≤ i ≤ k), such that

1. 1 ≤ k ≤ 3
2. p_i is a prime
3. 

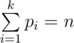
The numbers p_i do not necessarily have to be distinct. It is guaranteed that at least one possible solution exists.

Input

The single line contains an odd number n (3 ≤ n < 10⁹).

Output

In the first line print k (1 ≤ k ≤ 3), showing how many numbers are in the representation you found.

In the second line print numbers p_i in any order. If there are multiple possible solutions, you can print any of them.

Examples

Input

27

Output

3
5 11 11

Note

A prime is an integer strictly larger than one that is divisible only by one and by itself.

题意：

1. 1 ≤ k ≤ 3
2. p_i is a prime
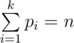3.        输出这n个数

题解：

      n为奇数    所有的素数 除了2  都是奇数   奇数+奇数=偶数   奇数+偶数=奇数

     1.若n为素数  则输出n

     2.若n-2为素数  则输出 2 n-2

     3. 其余的暴力 定第一个数为3  找到满足条件的  i  n-i-3

#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#include<stack>
#include<cmath>
#define ll __int64 
#define pi acos(-1.0)
#define mod 1000000007
using namespace std;
int n;
bool fun(int exm)
{
    if(exm<=1)
    return false; 
    for(int i=2;i*i<=exm;i++)
    {
        if(exm%i==0)
        return false;
    }
    return true;
}
int main()
{
    scanf("%d",&n);
    if(fun(n))
    {
        cout<<"1"<<endl<<n<<endl;
        return 0;
    }
    if(fun(n-2))
    {
        cout<<"2"<<endl<<"2 "<<n-2<<endl;
        return 0;
    }
    for(int i=3;i<=n-3;i++)
    {
        if(fun(i)&&fun(n-3-i))
          {
              cout<<"3"<<endl<<"3 "<<i<<" "<<n-3-i<<endl;
              return 0;
          }
    }
    return 0;
}